| Autor |
Beitrag |
    
Viper1986 (Viper1986)

Neues Mitglied
Benutzername: Viper1986
Nummer des Beitrags: 1
Registriert: 06-2004
| | Veröffentlicht am Samstag, den 12. Juni, 2004 - 11:23: | 
|
Ganz ganz wichtig! Eilt sehr! Bitte helft mir. Hab diese Aufgabe bekommen und hab keine Idee wie ich sie lösen kann. Vielleicht könnt ihr mir ja paar Hilfestellungen geben. Wäre voll lieb!!!!
Für jedes a ungleich 0 ist eine Funktion fa, gegeben durch
fa(x)=x:a+a+a: (x-a); x ungleich a.
Ihr Schaubild sei K(a)
a) Untersuche K(a) auf Asymptoten, Hoch-, Tief- und Wendepunkte.
Zeige, daß K(a) punktsymmetrisch zum Schnittpunkt S der beiden Asymptoten
ist.
Zeichne K(2) im Bereich —6 kleinergleich x kleinergleich 6.
b) Die Gerade g(a) geht durch die Extrempunkte der Kurve K(a).
Welche Beziehung muß zwischen a1, und a2 bestehen, damit sich die Geraden g(a1) und g(a2) rechtwinklig schneiden?
Berechne für diesen Fall die Koordinaten des Schnittpunktes der beiden Geraden.
c) Bestimme die Anzahl der Tangenten, die man von P(0|2) aus an die Kurve K(2) legen kann.
Die y-Achse, die Gerade y=-3/2x+2 und die Kurve K(2) umschließen eine Fläche.Berechne ihren Inhalt.
d) An K(a), sollen zwei zueinander parallele Tangenten gelegt werden.
Für welche Tangentensteigungen m ist dies möglich?
Die Berührpunkte dieser Tangenten sind Endpunkte einer Strecke.
Untersuche, ob es Werte von m gibt, für die der Mittelpunkt dieser Strecke auf der Geraden y = mx liegt.
|
    
Suddenguest (Suddenguest)

Junior Mitglied
Benutzername: Suddenguest
Nummer des Beitrags: 13
Registriert: 05-2004
| | Veröffentlicht am Sonntag, den 13. Juni, 2004 - 19:42: | 
|
Hallo.
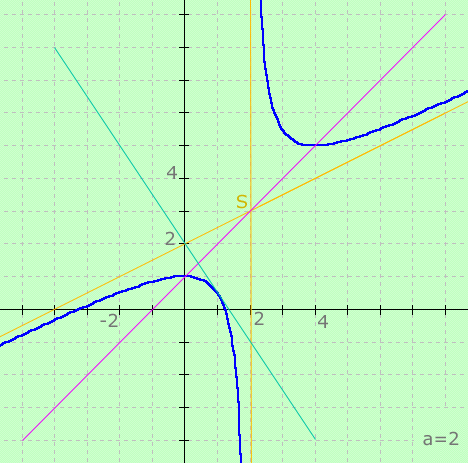
a)
f(x)=x/a+a+a/(x-a) x=/=a
f'(x)=1/a-a/(x-a)²
f''(x)=2a/(x-a)³
y=x/a+a schiefe Asymptote
x=a vertikale Asymptote
f'(x)=0
x1=0 Hoch
x2=2a Tief
Keine Wendepunkte, (Polstelle x=a)
Schnittpunkt S:
x=a
y=a/a+a=a+1
Funktion f(x) in neuen Koordinaten y => y+(a+1), x => x+a:
y+(a+1)=(x+a)/a+a+a/(x-a+a)
y=(x+a)/a+a/x-1=...=(x²+a²)/ax
y(-x)=-y(x) => punktsymmetrisch zum Schnittpunkt S.
b)
f(0)=a-1
f(2a)=a+3
Steigung=(y2-y1)/(x2-x1)=[a+3-(a-1)]/(2a-0)=4/2a=2/a
Beziehung zwischen a1, und a2, damit sich die Geraden g(a1) und g(a2) rechtwinklig schneiden:
m2=-1/m1 (allgemein)
hier: 2/a1=-a2/2 => a1*a2=-4
c)
Eine Tangente.
Fläche als Integral
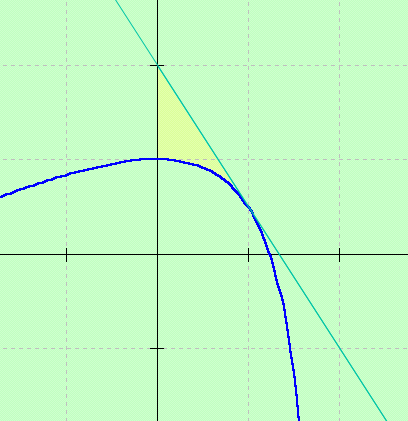
d) parallele Tangenten
f'(x)=m
1/a-a/(x-a)²=m
(x-a)²-a²=ma(x-a)²
(x-a)²=a²/(1-ma)
x=a[1+-1/sqrt(1-ma)] , ma<1
Die Berührpunkte dieser Tangenten sind Endpunkte einer Strecke.
Untersuche, ob es Werte von m gibt, für die der Mittelpunkt dieser Strecke auf der Geraden y = mx liegt.
-- Keine Ahnung :-(
tschüs
|
|