| Autor |
Beitrag |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 6
Registriert: 03-2005
| | Veröffentlicht am Samstag, den 19. März, 2005 - 20:50: | 
|
Hi, es geht hier um eine Übungsaufgabe, bei der ich nicht so ganz durchblicke:
Von einem regelmäßigen Tetraeder kennt man die Trägergeraden g und h zweier gegenüberliegender Kanten.
Welche Lage müssen diese Geraden zueinander haben? Prüfe nach, ob dies tatsächlich der Fall ist! Berechne anschließend die Koordinaten des Mittelpunktes und das Volumen des Tetraeders!
g: X=(0;-1;-9)+s*(8;3;5)
h: X=(17;-16;12)+t*(4;-9;-1)
Das Volumen ist das geringste Problem! 
Danke schon jetzt für eine Unterstützung!
corvus_ |
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 1208
Registriert: 05-2002
| | Veröffentlicht am Samstag, den 19. März, 2005 - 22:06: | 
|
in Summe hat ein Tetraeder 6 Kanten, da es um einen regelmäßigen Tetraeder geht müssen die Kanten Paarweise einen Winkel von pi/3 einschließen;
um dies nachzuprüfen verwende man folgende Beziehung
cos( phi ) = ( a * b ) / ( |a| * |b| )
also
cos( phi ) = ( (8;3;5) * (4;-9;1) ) / ( |(8;3;5)| * |(4;-9;1)| )
cos( phi ) = ( 32 - 27 + 5 ) / ( 7 sqrt( 2 ) * 7 sqrt( 2 ) ) = 10 / 98
cos( pi/3 ) = 1/2
entweder es ergibt tatsächlich keinen regelmäßigen Tetraeder oder es liegt ein Fehler in der Angabe vor;
(Beitrag nachträglich am 19., März. 2005 von mainziman editiert)
Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 7
Registriert: 03-2005
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 07:28: | 
|
Hi, in der Angabe liegt hoffentlich kein Fehler vor, abgetippt ist sie zumindest richtig!
Meine Überlegung:
Gegenüberliegende Kanten liegen auf windschiefen Geraden, daher dürfen g und h keinen Schnittpunkt haben – und sie haben auch keinen! Nur wie komme ich bei dieser Angabe auf ein vernünftiges Tetraeder? Die Kanten sind alle gleich lang, aber damit komme ich nicht weiter. Ich hoffe weiter auf einen Geistesblitz oder auf Hilfe von einem Durchblickenden!
Corvus_ |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 2734
Registriert: 02-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 08:06: | 
|
das Skalarprodukt der Richtungsvektoren von g,h
ist 0, sie sind also normal zueinander.
Denk an einen Würfel, von einer Ecke ausgehend
die Flächendiagonalen eingezeichnet, deren andere
Enden verbunden sind wieder Flächendiagonalen.
Diese 6 Strecken bilden einen regelmäßigen Tetraeder, die Kanten auf gegenüberligenden Würfel-
flächen sind einander normal kreuzende windschiefe.
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4898
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 08:19: | 
|
Hi Corvus

Die Antwort von Friedrich trifft ins Schwarze!
Bestimnme den kürzesten Abstand der Geraden g und h nach Lage und Grösse k.
k stimmt mit der Kantenlänge des von Friedrich genannten Würfels überein!
die Tetraederkante hat die Länge der Flächendiagonalen des Würfels.
MfG
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4900
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 09:13: | 
|
Hi Corvus

Als erstes musst Du die so genannte
Minimaltransversale von g und h
ermitteln.
Gemeint ist das Folgende:
Es seien zwei windschiefe Geraden g und h gegeben.
Es gibt dazu genau eine Gerade t, welche g und h
je senkrecht schneidet;
Schnittpunkt (t, g) = G , (t, h) = H.
Der Abstand der Punkte G und H ist der
kürzeste Abstand k von g und h.
Die Gerade t heißt daher „Minimaltransversale“
von g und h.
Die Bestimmung der Minimaltransversalen ist
in diesem Forum mehrmals vorgeführt worden;
siehe im Archiv nach.
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 8
Registriert: 03-2005
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 09:25: | 
|
Vielen Dank vorerst! Ich muss mir das an einer Skizze veranschaulichen, im Moment habe ich große Vorstellungsprobleme!
corvus_ |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4901
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 09:36: | 
|
Hi Walter
Bei Deiner Berechnung des Skalarprodukts hat sich ein Fehler eingenistet.
Das Skalarprodukt ist in Tat und W . null,
wie es bei regulären Tetraedern für gegenüberliegende Kanten sein muss.
Ich selbst bin es gewöhnt,Rechen- und namentlich
Tippfehler zu machen.
Das wissen meine Leser a priori und richten sich
entsprechend ein.!
Wir haben nun also die Situation gerettet
und sehen zu,was Corvus damit anfängt
MfG
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4902
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 09:45: | 
|
Hi corvus

Zeichne den Würfel,den Friedrich erwähnt hat.
In gegenüber liegenden Seitenflächen zeichnest Du Flächemdiagonalen AB im einen,CD im andern Quadrat so, dass diese Diagonalen nicht parallel,sondern orthogonal sind.
Dann hast Du in A,B,C,D schon die
Ecken des regulären Tetraeders,hihi
MfG
H.R.Moser,megamath |
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 1210
Registriert: 05-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 10:58: | 
|
Hi Megamath,
jetzt am Morgen seh ich es, 'nen Vorzeichenfehler hat sich eingeschlichen 
Ach, des sind ja 2 windschiefe Geraden;
ergibt da nicht der kürzeste Abstand etwas "brauchbares" (Kantenlänge?) und der Halbierungspunkt des Abstands (Mittelpunkt der umschreibenden Kugel)? 
Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4903
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 12:05: | 
|
Hi corvus

Die Überlegungen von Walter treffen zu!
Du bekommst den gesuchten Mittelpunkt M
als Mittelpunkt der Stecke GH auf der
Minimaltransversalen.
Wenn Du willst, kann ich Dir die Ermittlung der
Minimaltransversalen an einem früheren Beispiel
(mit anderen Koordinaten) vorführen.
Bist Du so sicher, dass die Ermittlung des Volumens V
des Tetraeders kein Problem sein soll und nur ein
Sonntagsspaziergang ist?
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4904
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 14:09: | 
|
Hi corvus corax

Meine konzentrierte Wortmeldung ergibt sich daraus,
dass ich heute Abend verhindert sein werde,
im Forum zu arbeiten.
Hier denke ich noch etwas laut über das Volumen
des Tetraeders nach.
Dies lässt sich auf mannigfache Weise bestimmen,
wenn man den Würfel von Fritz samt eingebautem
Tetraeder einmal im Griff hat.
Sei k die Länge der Würfelkante.
(es wird sich zeigen, Irrtum vorbehalten, k = 15)
Dann bekommst Du die Länge a einer Tetraederkante
ganz einfach als Länge einer Flächendiagonalen
des Würfels, also a = k * wurzel(2).
Daraus kann man das Volumen mit einer fertigen Formel
berechnen:
V = 1/12 * a^3 * wurzel(2)
oder:
Das Volumen des dem Würfel eingebauten Tetraeders
ist der sechste Teil des Würfelvolumens.
V = 1/6 * k^3
oder:
Ich fasse den Tetraeder als Prismatoid auf;
Höhe h = k
Grundfläche G = 0, Deckfläche D = 0 null,
Mittelschnitt M : der vierte Teil einer Würfelfläche,
also
M = ¼ k^2
V = h/6 * (G + 4 M + D)
usw
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 9
Registriert: 03-2005
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 14:22: | 
|
Danke für die Bemühungen um meine Aufgabe!
Ich versuche noch immer, anhand meiner Skizze eine Vorstellung von der Situation zu bekommen. Für die Tetraederkantenlänge habe ich denselben Wert. Meine Skizze ist auch korrekt, nur mit anderen Bezeichnungen. Nun möchte ich einzeichnen, skizzieren, wie ich zum Mittelpunkt komme, das gelingt mir nicht. Mit fertigen Formeln rechne ich nicht gerne!
Aber trotzdem vielen Dank!
corvus_ |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 10
Registriert: 03-2005
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 14:29: | 
|
Auch muss ich doch irgendwie Koordinaten für die Eckpunkte oder dergleichen bekommen, weil ich ja dann auch die Koordinaten für den Mittelpunkt M brauche. Ich meine: ich kann ja nicht einfach mit der Kantenlänge weiterrechnen, das Ganze hat ja einen bestimmten Ort! Und das macht mir Schwierigkeiten.
corvus_ |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4905
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 17:41: | 
|
Hi Corax

Ich zeige Dir den Anfang Deiner Aufgabe anhand
eines andern Zahlenbeispiels.
Wenn Du dann auf analoge Weise bei Deiner Aufgabe
den Punkt G auf g und H auf h gefunden hast, trage
auf g von G aus ½ a nach beiden Seiten bis A
bzw. B ab, auf h von H aus ½ a nach beiden Seiten
bis C bzw. D .
Du bekommst a aus der Beziehung a = k * wurzel(2);
k ist die Länge der Strecke GH.
Das lässt sich rechnerisch leicht nachvollziehen.
Veröffentlicht am Donnerstag, den 03. Juni, 2004 - 20:48:
Frage:
Ich hab da ein Problem.
gegeben sind die zwei geraden
g: x=(2;1;5)+t(1;0;3)
h: x=(3;4;2)+t(-1;4;1)
die Aufgabe ist nun, ich soll den Punkt G auf g
und H auf h so bestimmen, dass die Strecke GH genauso
lang ist wie der Abstand von g und h.
Veröffentlicht am Donnerstag, den 03. Juni, 2004 - 21:34:
Antwort:
Es handelt sich bei Deiner Aufgabe um die Ermittlung der
so genannten Minimaltransversalen mm der gegebenen
windschiefen Geraden g und h.
Die Gerade mm schneidet g und h je senkrecht,
und zwar g im Punkt G, h im Punkt H.
Der Abstand dieser beiden Punkte ist der kürzeste Abstand d
der beiden windschiefen Geraden.
Im vorliegenden Fall ergibt sich das Resultat:
G : xG = 12/11, yG = 11/11, zG =25/11
H : xH = 39/11, yH = 20/11, zH =16/11
Der Abstand ist d = 1/11* sqrt(891) = 9/sqrt(11) ~ 2,7136
Dieses Resultat erhält man auch mit der Formel, in deren
Zähler ein gewisses Spatprodukt und im Nenner der Betrag
eines gewissen Vektorprodukts stehen.
Herleitung der Minimaltransversalen mm.
Bezeichnungen:
a ist der gegebene Richtungsvektor von g:
a = {1;0;3},P der laufende Punkt auf g, Parameter t
b ist der gegebene Richtungsvektor von g:
b = {-1;4;1},Q der laufende Punkt auf h ,Parameter r
Wir ermitteln die drei Koordinaten des Verbindungsvektors
v = PQ; dieser Vektor ist der Differenzvektor der
Ortsvektoren der Punkte Q und P, also:
v = {3 - r - 2 - t ; 4 + 4 r - 1 ; 2 + r - 5 - 3 t }
Da die Transversale mm sowohl auf g als auch auf h senkrecht
steht, sind die beiden folgenden Skalarprodukte null.
v . a = 0
v . b = 0
Es entstehen die folgenden beiden Gleichungen
zur Ermittlung der Parameterwerte t und r:
r -5 t - 4 = 0
9 r - t + 4 = 0
Daraus t = - 10 / 11 , r = - 6 / 11
Damit erhält man die angegebenen Punkte
und den erwähnten kürzesten Abstand.
Soweit das Zitat aus früheren Zeiten
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 11
Registriert: 03-2005
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 19:28: | 
|
Hi megamath, und danke für Deine Bemühung, aber es ist hoffnungslos.
Ich habe von Anfang an andere Bezeichnungen gewählt, wie ich sie gewohnt bin,
G ist der gegebene Punkt auf g und vektor(g) der Richtungsvektor,
H ist der gegebene Punkt auf h und vektor (h) der Richtungsvektor,
a ist meine Würfelkante und k meine Tetraederkante,
drum wählte ich jetzt A und B für die Punkte, die den kürzesten Abstand haben sollen.
Aber an Bezeichnungen alleine kann es ja nicht liegen!
Vielleicht habe ich mich auch verrechnet:
s=2 und t=13/7. daher ist A(16;5;1)aus g und B(171/7;5/7;71/7) aus h, und weiter komme ich nicht.
Eines will mir nicht in den Kopf:
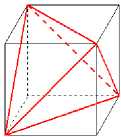
Die beiden Geraden g und h laufen doch sozusagen durch die Basisfläche und die Deckfläche eines Würfels (wobei die Richtungsvektoren aufeinander senkrecht stehen),
das bedeutet doch, dass sie überall den gleichen Abstand haben, weil doch diese beiden Flächen parallel sind. Warum rechne ich dann einen Minimalabstand aus???
Der Würfel am Bild hat die Ecken ABCD EFGH (A ist links unten, vorne),
das ist meine Gedankenstütze.
Danke nochmals,
corvus_
 |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4906
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 20:02: | 
|
Hi Corvus

Ich habe mich schnell aus einer Gesellschaft entfernt, um
Dir zu sagen,dass bei Deinen Lösungsversuchen noch lange nicht alles verloren ist .
Ich komme morgen auf die Aufgabe zurück
und versuche,den Knoten zu lösen
Für die kritischen Punkte kommt bei mir s = 2 und t = minus 13/7.
Jetzt muss ich zurück !
MfG
H.R.Moser,megamath |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 12
Registriert: 03-2005
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 20:22: | 
|
Danke, war ein Vorzeichenfehler meinerseits.
Auch wenn die Rechnung nun stimmt, weiß ich nicht, warum das alles so ist! Vielleicht geht mir morgen ein Licht auf!
corvus_ |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4907
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 20. März, 2005 - 22:01: | 
|
Hi corvus.

Damit Klarheit besteht:
ich halte mich an meine Bezeichnungen, nicht aus
Eigenwilligkeit, sondern aus meiner Interessenlage heraus,
eine gute Erklärung zu finden.
Ich bin schon auch der Meinung,
dass man nicht mitten im Rennen das Pferd wechseln soll;
ferner sollten wir Lehrenden es den Studierenden möglichst
einfach machen, indem wir uns möglichst an die
Bezeichnungen halten, an die sie gewöhnt sind.
Andrerseits kann eine harte Schule beim Studium nichts
schaden und die Aufmerksamkeit nur fördern..
Zu meinen Zeiten in den Vorlesungen der theoretischen Physik,
hat mein verehrter Professor Wolfgang Pauli gelegentlich
(an besonders schwierigen Stellen) mit der linken Hand
ausgewischt, was er soeben mit der rechten geschrieben hatte.
1.
Die Ecken des Würfels tragen am Anfang gar keine
Bezeichnungen!
(NCHT A,B,C,D E,F,G H).
2.
Alles läuft darauf hinaus, auf der Geraden g den Punkt G,
auf der Geraden h den Punkt H zu finden und zwar
derart, dass die Verbindungsgerade GH auf g und auf h
zugleich je senkrecht steht; das ist die berühmte
Minimaltransversale mm.
Beim famosen Würfel findest Du diese Punkte leicht:
G ist der Mittelpunkt der Deckfläche des Würfels
H ist der Mittelpunkt der Grundfläche des Würfels.
3.
Die Kantenlänge des Würfels soll mit k bezeichnet werden.
Dann gilt k = Länge der Strecke GH;
dies ist der kürzeste Abstand der windschiefen Geraden
g und h, wie man sagt „nach der Größe“.
Er ergibt sich auch sofort als Abstand der beiden
genannten Seitenflächenebenen des Würfels.
Bei gewissen Aufgaben kann man sich mit diesem
Abstand begnügen und braucht nicht mm mit den
Schnittpunkten G und H zu bestimmen.
Beim anstehenden Problem ist mm unerlässlich.
4.
Mit Hilfe der Würfelkante k ermittelt man die
Länge der Tetraederkante a.
Eine solche Kante hat dieselbe Länge wie eine
Flächendiagonale des Würfels; dies ist leicht einzusehen:
a = k* sqrt(2)
5.
Wie gewinnt man nun den Tetraeder selbst?
Das Gerüst und sogar der Rohbau sind fertig!
Man trage die halbe Kantenlänge a/2 des T. auf g
einerseits von G aus auf g in beide Richtungen von g ab:
Du bekommst als Endpunkte die Tetraederecken A und B.
Man trage ferner die halbe Kantenlänge a/2 des T. auf h
andrerseits von H aus auf h in beide Richtungen von h ab:
Du bekommst als Endpunkte die Tetraederecken C und D.
Der gesuchte Tetraeder ist fertig.
Der gesuchte Mittelpunkt M des Tetraeders ist zugleich
der Mittelpunkt des Würfels.
6.
Deine Skrupel sind bald ausgeräumt.
Nur gerade das Punktepaar G und H, das wir mit Hilfe
des Orthogonalitätsprinzips (Skalarprodukt null)
ermittelt haben, erfüllt die gestellte Bedingung,
dass die Gerade mm SOWOHL auf g
ALS AUCH auf h zugleich senkrecht steht.
Da ist die Tatsache, dass g und h in parallelen Ebene liegen,
irrelevant. Dies lässt sich für alle Paare windschiefer Geraden
einrichten.
Der Abstand dieser parallelen Ebenen ist der kürzeste Abstand,
nicht mehr, aber auch nicht weniger.
So weit ein paar Noterklärungen.
Auch hier:
Schwamm drüber!
Die ganze Rechnung soll morgen
ab ovo pro corvo
durchgeführt werden
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4909
Registriert: 07-2002
| | Veröffentlicht am Montag, den 21. März, 2005 - 13:46: | 
|
Hi Corvus

Es folgt die Herleitung der Minimaltransversalen mm
für das von Dir vorgelegte numerische Beispiel.
Gegeben sind die zwei windschief normalen Geraden
g: X=(0;-1;-9)+s*(8;3;5)
h: X=(17;-16;12)+t*(4;-9;-1)
Die gesuchte Gerade mm schneidet g und h je senkrecht,
und zwar g im Punkt G, h im Punkt H.
Der Abstand dieser beiden Punkte ist der kürzeste Abstand
d der beiden windschiefen Geraden.
Im vorliegenden Fall ergibt sich das Resultat:
G : xG = 16, yG = 5, zG =1
H : xH = 67/7, yH = 5/7, zH =97/7
Der Abstand ist
d =1/7 *sqrt [45^2+30^2+90^2] = 15/7 * sqrt(49) = 15
Dieses Resultat erhält man auch mit der Formel, in deren
Zähler ein gewisses Spatprodukt und im Nenner der Betrag
eines gewissen Vektorprodukts stehen.
Herleitung der Minimaltransversalen mm.
Bezeichnungen:
a ist der gegebene Richtungsvektor von g:
a = {8;3;5}, P der laufende Punkt auf g, Parameter s
b ist der gegebene Richtungsvektor von g:
b = {4;-9;-1}, Q der laufende Punkt auf h ,Parameter t
Achtung:
Die beiden Parameter dürfen nicht mit demselben Symbol
bezeichnet werden, da sie unabhängig voneinander variieren!
Wir ermitteln die drei Koordinaten des Verbindungsvektors
v = PQ; dieser Vektor ist der Differenzvektor der
Ortsvektoren der Punkte Q und P, also:
v = {17 + 4 t – 8 s ;- 15 - 9 t – 3 s; 21 – t – 5 s}
Da die Transversale mm sowohl auf g als auch auf h senkrecht
steht, sind die beiden folgenden Skalarprodukte null.
v . a = 0
v . b = 0
Es entstehen die folgenden beiden Gleichungen
zur Ermittlung der Parameterwerte s und t:
196 – 98 s = 0
182 + 98 t = 0
Daraus t = - 13/7 , s = 2
Damit erhält man die angegebenen Punkte G und H.
Die Koordinaten des Mittelpunktes der Strecke GH
sind beziehungsweise die arithmetischen Mittel der
Koordinaten der Endpunkte.
Man erhält:
xM = 179/14 ; yM = 20/7 ; zM = 52/7.
Aus der Kantenlänge k = GH = 15 des Würfels berechnet
man die Katenlänge a des Tetraeders
a = k*sqrt(2) = 15 * sqrt(2).
Das Volumen V ergibt sich aus dem Würfelvolumen
V = 1/6 * k^3 = 1/6 * 15^3 = 562,5
In einem nächsten Beitrag sollen noch die Koordinaten
der Ecken A,B,C,D des Tetraeders bestimmt werden.
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 13
Registriert: 03-2005
| | Veröffentlicht am Montag, den 21. März, 2005 - 17:36: | 
|
Guten Abend und vielen Dank für die ausführliche Herleitung!
Das Volumen des Tetraeders ist meines Erachtens aber nicht 1/6 des Würfelvolumens, sondern 1/3 davon, also 1125.
Dasselbe Resultat erhält man mit der Formel: V = 1/12 * a^3 * wurzel(2), wobei a die Kantenlänge des Würfels ist.
Eigentlich müsste man das Volumen auch mittels Spatprodukt errechnen können!?
Noch nicht ganz klar ist mir, warum der Mittelpunkt des Tetraeders mit dem Mittelpunkt der Strecke GH zusammenfällt, obwohl es rein gefühlsmäßig einleuchtet – aber das ist ja kein Beweis!
Vielen Dank!
Corvus_ |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4913
Registriert: 07-2002
| | Veröffentlicht am Dienstag, den 22. März, 2005 - 10:29: | 
|
Hi Corvus

Du hast Recht:
das Volumen des nun bald überstrapazierten
Tetraeders beträgt 1125 Volumeneinheiten,
insbesondere macht das dem Würfel eingelagerte
Tetraedervolumen den DRITTEN Teil
des Würfelvolumens aus.
Sollen die Koordinaten der Tetraederecken noch
explizit berechnet werden?
Liegen diese einmal vor, kann zur Kontrolle der
Volumenrechnung das bekannte gemischte Produkt
berechnet werden; hier kommt dann aber der Divisor
SECHS zum Zug!
Bezüglich der Rolle des Punktes M wäre einiges zu sagen.
Es handelt sich um den Schwerpunkt des Tetraeders.
Schon für den allgemeinen Tetraeder gibt es diesbezüglich
interessantes zu Erzählen.
Auf Wunsch werde ich dies gerne tun.
Im Moment nur das:
Die drei Verbindungsgeraden der Gegenkantenmitten
im allgemeinen Tetraeder gehen durch den Schwerpunkt
des Tetraeders und werden durch diesen halbiert
(da haben wir es !).
Im regulären Tetraeder fallen der Höhenschnittpunkt,
der Mittelpunkt der Umkugel und der Mittelpunkt der Inkugel
mit dem Schwerpunkt zusammen.
usw.
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 14
Registriert: 03-2005
| | Veröffentlicht am Dienstag, den 22. März, 2005 - 19:24: | 
|
Guten Abend!
Die Tetraederecken interessieren mich schon auch noch, auch die besonderen Eigenschaftes des Tetraeders, aber ich möchte hier niemand über Gebühr strapazieren!
vielen Dank und Grüße
corvus_ |
    
Elsa13 (Elsa13)

Erfahrenes Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 108
Registriert: 12-2002
| | Veröffentlicht am Donnerstag, den 31. März, 2005 - 09:18: | 
|
Corvus,
hier also noch die Berechnung der Eckpunkte des Tetraeders und des Volumens:

liebe Grüße
elsa
(Beitrag nachträglich am 31., März. 2005 von elsa13 editiert) |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 15
Registriert: 03-2005
| | Veröffentlicht am Donnerstag, den 31. März, 2005 - 18:59: | 
|
Vielen Dank, elsa, nun kann ich dieses Beispiel abhaken!
Ich wollte nicht ungeduldig erscheinen und noch einmal nachfragen, megamath hatte ja am 21. März angekündigt, die Eckpunkte zu berechnen.
Viele Grüße
corvus_ |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4947
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 31. März, 2005 - 19:20: | 
|
Hi Corvus

Ich hatte sie auch berechnet,wurde aber
anderweitig in Anspruch genommen,und wie!
Ich habe die jetzt vorliegenden Beiträge ganz aus den Augen verloren
Ich bitte um Entschuldigung!
Haupsache: elsa hat die Aufgabe
souverän zu einem guten Ende geführt!
MfG
H.R.Moser,megamath |
    
Corvus_corax (Corvus_corax)

Junior Mitglied
Benutzername: Corvus_corax
Nummer des Beitrags: 16
Registriert: 03-2005
| | Veröffentlicht am Freitag, den 01. April, 2005 - 06:30: | 
|
Hallo megamath,
keine Ursache! Es ist ja nun gelöst!
Gruß
corvus_ |
|