| Autor |
Beitrag |
    
Nic (Nic)

Mitglied
Benutzername: Nic
Nummer des Beitrags: 17
Registriert: 12-2002
| | Veröffentlicht am Freitag, den 31. Oktober, 2003 - 13:33: | 
|
Hallo! Brauche unbedingt Hilfe bei diesem Beispiel: Wie berechnet man das òcos^n(x).dx?
nic |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 1626
Registriert: 02-2002
| | Veröffentlicht am Freitag, den 31. Oktober, 2003 - 13:39: | 
|
durch mehrfache partielle Integration,
bis
schliesslich co²x = (1 + cos(2x))/2
verwendet werden kann.
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Heavyweight (Heavyweight)

Erfahrenes Mitglied
Benutzername: Heavyweight
Nummer des Beitrags: 283
Registriert: 09-2002
| | Veröffentlicht am Freitag, den 31. Oktober, 2003 - 21:22: | 
|
Hi,also:
òcosn(x)dx=[cosn-1(x)*sin(x)]/n+(n-1)/n*òcosn-2(x)dx
(n¹0)
Gruß,Olaf |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 2901
Registriert: 07-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 10:38: | 
|
Hi Olaf

Die Fragen von nic möchte ich etwas eingehender beantworten
als bisher geschehen.
Du hast dabei gute Vorarbeit geleistet; der erste Schritt
mit partieller Integration liefert dieses schöne Resultat,
bei welchem der Exponent von cos(x) im Integral rechts
um eine Zwei verringert wird.
Im Sinne einer Rekursion erhält man zum Beispiel
die Folge:
int [(cos x)^8 dx] = 1/8{cos(x)}^7 sin x+7/8 int [(cos x)^6 dx]
int [(cos x)^6 dx] = 1/6{cos(x)}^5 sin x+5/6 int [(cos x)^4 dx]
int [(cos x)^4 dx] = ¼ {cos(x)}^3 sin x+ ¾ int [(cos x)^2 dx]
int [(cos x)^2 dx] = ½ cos(x) sin x+ ½ x
Berechne in analoger Weise die Integrale über cos(x)
mit den Exponenten 7 , 5 , 3 , 1
Wichtige Bemerkung.
Bei ungeraden Exponenten n = 2m+1 geht man mit
Vorteil anders vor ,hihi!
Ersetze im Integranden (cosx)^2 durch1 – (sinx)^2 ,
substituiere sin x = z , cos x dx = dz.
Beispiel: n= 7
int [(cos x)^7 dx] = int [{1- (sin x)^2}^3 * cos x dx]
= int[{1 - z^2 }^ 3 dz ] = int [{1 – 3 z^2 + 3 z^4 – z^6} dz =
= z – z^3 + 3/5 z^5 - 1/7 z^7; ersetze nun z durch sin x
voilà !
Bitte auf Tippfehler überprüfen!
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Nic (Nic)

Mitglied
Benutzername: Nic
Nummer des Beitrags: 18
Registriert: 12-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 11:59: | 
|
Vielen Dank für eure Hilfe!
Ihr wisst ja gar nicht wie sehr ihr mir geholfen habt! 
Vlg
nic |
    
Heavyweight (Heavyweight)

Erfahrenes Mitglied
Benutzername: Heavyweight
Nummer des Beitrags: 284
Registriert: 09-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 16:43: | 
|
Hi Megamath,
Das sieht ja mal wieder sehr interessant aus!
Werde ich mir später genauer ansehen.
Gruß,Olaf |
    
Heavyweight (Heavyweight)

Erfahrenes Mitglied
Benutzername: Heavyweight
Nummer des Beitrags: 285
Registriert: 09-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 20:45: | 
|
Hi Megamath,
Das ist ja echt clever,danke!
Gruß,Olaf |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 2906
Registriert: 07-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 20:50: | 
|
Hi Olaf,
es wird noch cleverer, hihi !
  
Ein wenig Geduld noch!
MfG
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 2907
Registriert: 07-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 21:10: | 
|
Hi Olaf

Richtig interessant wird die Angelegenheit, wenn
wir die bestimmten Integrale von {cos(x)}^n
in den Grenzen 0 bis ½ Pi rechnen!
für gerade n (even integer) kommt als Resultat:
even (n) = [1*3*5*…*(n-1)] / [2*4*6*..*n] * ½ Pi
für ungerade n (odd integer) kommt als Resultat:
odd (n) = [2*4*6*…*(n-1)] / [1*3*5*..*n]
In einem nächsten Beitrag sollen even (4) und
odd(3) berechnet werden.
Zur Bestätigung wird die Gammafunktion ins Spiel
gebracht.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 2908
Registriert: 07-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 21:39: | 
|
Hi Olaf

Es zeigt sich, dass man mit Hilfe der Gammafunktion
GAMMA (x)
die in der letzten Arbeit erwähnten Werte even (n) und odd (n)
sehr elegant ausdrücken kann.
Es gilt für beide Fälle (Bezeichnung Y(n) , n> -1);
alles steckt nun unter einem Hut, eben der Gammafunktion:
Y(n) = ½ sqrt(Pi) * GAMMA [½(n+1)] / GAMMA [½n + 1]
Wir benötigen drei Gamma-Werte.
GAMMA(2) = 1! = 1
Gamma(3) = 2! = 2
GAMMA (2,5) = ¾ *sqrt(Pi)
Das genügt vollauf; wir rechnen
odd(3) = (2 * 4) / (1 * 3 ) = 2/3
Y(3) = ½ sqrt (Pi) * GAMMA(2) / Gamma(2,5) = 2/3, bravo!
even(4) = (1 * 3) / (2 * 4 ) * ½ Pi = 3/16 * Pi
Y(4) = ½ sqrt (Pi) * GAMMA(2,5) / Gamma(3) =3/16 * Pi, bravo!
Es ist reizvoll, via Gammafunktion
Y(3) * Y(4) zu berechnen;
GAMMA(2,5) fällt aus der Rechnung, hihi !
Resultat:
Y(3)*Y(4) = Pi / 8, ein herrliches Resultat,
das im Verein der Freunde der Zahl Pi in Wien
kaum bekannt sein dürfte.
MfG
H.R.Moser,megamath
|
    
Heavyweight (Heavyweight)

Erfahrenes Mitglied
Benutzername: Heavyweight
Nummer des Beitrags: 286
Registriert: 09-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 21:50: | 
|
Hi Megamath,
Super,das werde ich morgen genau studieren!
Gruß,Olaf |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 1631
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 21:55: | 
|
zur Stammfunktion sollte man der
Vollständigkeit halber auch nicht
vergessen daß
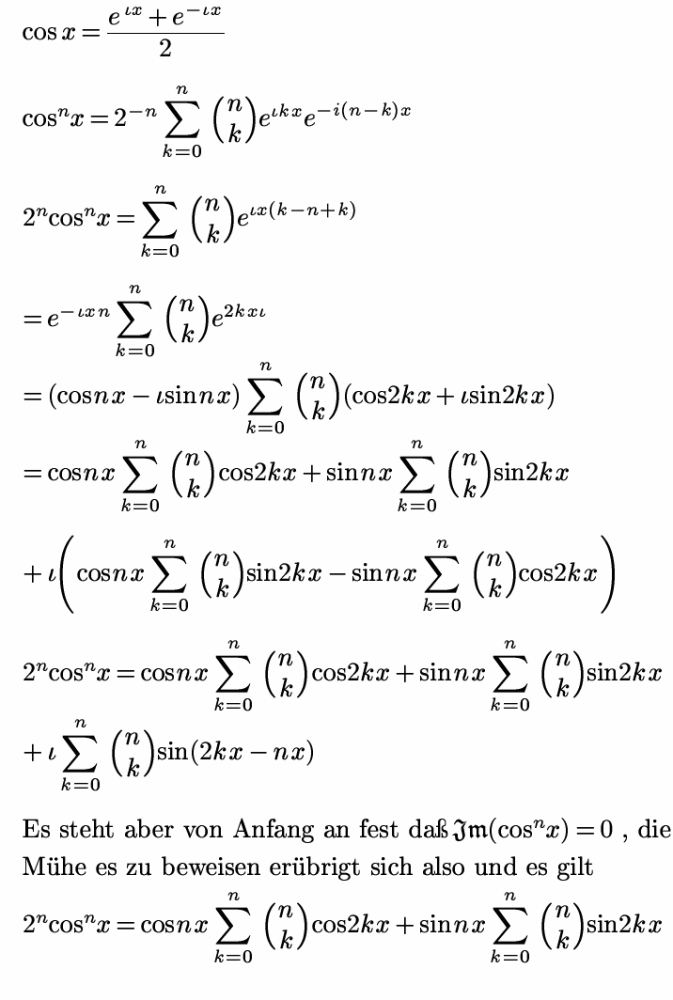
cosnx "geschlossen" dargestellt
werden kann.
Die Integration kann nun partiell
erfolgen,
oder man verwendet
cosu * cosv = +[cos(u+v) + cos(u-v)]/2
sinu * sinv = -[cos(u+v) - cos(u-v)]/2
(Beitrag nachträglich am 01., November. 2003 von friedrichlaher editiert)
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 915
Registriert: 10-2002
| | Veröffentlicht am Samstag, den 01. November, 2003 - 22:16: | 
|
Hi megamath,

Meine Anerkennung, das vereinfacht jetzt aber einiges! Wozu die Gammafunktion doch gut ist...
Ich frage mich nur woher du immer diese ganzen Sachen herholst, so ganz überraschend...
mfg
|
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 1632
Registriert: 02-2002
| | Veröffentlicht am Sonntag, den 02. November, 2003 - 06:19: | 
|
in meinem Beitrag vom 1.Nov. habe ich etwas zu
umständlich gerechnet, das Ergebnis hätte sich
sofort nach der 3ten Zeile ergeben weil
eix(k-n+k)=eix(2k-n)= cos(2k-n) + i*sin(2k-n)
also,
wie auch einfach durch Umkehranwendung von cos(u-v)
aus der letzen Zeile (2ncosn= ....)
hervorginge
cosnx = 2-nSumme[(n über k)cos(nx-2kx),k=0 bis n]
( ein Dumpfes Gefühl, ich könnte ein Dumpfes Gefühl, ich könnte
einen Fehler gemacht haben, hatte mich 10 nach 5 aus dem Bett getrieben)
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Heavyweight (Heavyweight)

Erfahrenes Mitglied
Benutzername: Heavyweight
Nummer des Beitrags: 287
Registriert: 09-2002
| | Veröffentlicht am Sonntag, den 02. November, 2003 - 10:54: | 
|
Hi,
@Friedrich
Danke für Deinen Beitrag,werde ich mir später auch genauer anschauen.
Zunächst muß ich mich aber etwas mehr mit der Gammafunktion vertraut machen,da habe
ich noch Nachholbedarf.
Gruß,Olaf |