| Autor |
Beitrag |
    
Lupo

| | Veröffentlicht am Donnerstag, den 12. Juli, 2001 - 16:02: | 
|
Hallo
ich hoffe ihr könnt mir was zu meinem Problem sagen.
Gegeben ist die Matrix A=
( 1 2 2)
( 0 2 1)
(-1 2 2).
Das charakteristische Polynom habe ich mit (1-t)(2-t)² ausgerechnet, der Eigenvektor zum Eigenwert 1 lautet (1,1,-1).
Ansatz, um den Eigenvektor (x,y,z) zum Eigenwert 2 herauszubekommen:
(-1 2 2)
( 0 0 1)
(-1 2 0)
geht über in
(-1 2 0)
( 0 0 1)
(-1 2 0)
und damit ergeben sich die Gleichungen x=2y und z=0.
Ein Eigenvektor lautet also (2,1,0).
Wie aber bekomme ich den dritten Eigenvektor raus?
Ich habe schon hier im Board nach vergleichbaren Problemen gesucht, die Rechnung in http://www.mathehotline.de/mathe4u/hausaufgaben/messages/4244/8141.html ist mir jedenfalls klar, aber irgendwie ist das wieder was anderes. |
    
Hans (Birdsong)

| | Veröffentlicht am Donnerstag, den 12. Juli, 2001 - 19:15: | 
|
Hallo:
Du hast richtig gerechnet. Der Eigenwert
lambda(2) = 2 ist aber eine 2-fache Nullstelle des
charaktristischen Polynoms, und man kann nicht
erwarten, dass dazu 2 linear unabhaengige Eigenvektoren existieren. Demgemaess laesst sich
A auch nicht diagonalisieren, d.h. es gibt keine
Matrix U derart dass U^(-1) A U = diag(1,2,2).
Das was der Diagonalform sozusagen am naechsten
kommt, ist die Jordan-Normalform
J=([1,0,0],[0,2,1],[0,0,2]),
etwas besseres gibt es hier nicht. Fr die durch
x--> A x beschriebene Abbildung des R^3 gibt es
eben nur 2 invariante Richtungen. Mach dir das
an einem ebenen Beispiel klar :
x' = x + y , y' = y.
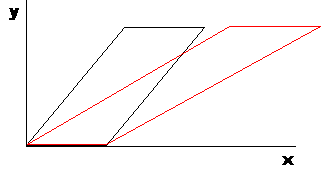
Das ist eine Scherung parallel zur x-Achse.Die
zugehoerige Matrix ([1,1],[0,1]) hat den 2-fachen
Eigenwert 1, und es gibt nur einen l.u. Eigenvektor (1,0), d.h. die einzigen Fixgeraden
sind die Parallelen zur x-Achse.
Gruss
Hans |
    
Lupo

| | Veröffentlicht am Donnerstag, den 12. Juli, 2001 - 23:31: | 
|
Hallo Hans, ich habe es verstanden.
so ein Beispiel wie das mit der Scherung hat mir gefehlt. Ich habe immer gedacht, bei einer 3x3-Matrix müsste man auch 3 Eigenvektoren erhalten können.
Freitag werde ich mir das mit der Jordan-Form mal genauer ansehen.
Wenn schon im Voraus noch eine kleine Frage erlaubt ist: Gibt es einen Unterschied zwischen "Normalform" und "Jordan-Normalform" einer Abbildung?
Aber erstmal vieeelen Dank dafür |
    
Lupo

| | Veröffentlicht am Donnerstag, den 12. Juli, 2001 - 23:34: | 
|
 |
|