| Autor |
Beitrag |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4198
Registriert: 07-2002
| | Veröffentlicht am Montag, den 21. Juni, 2004 - 15:38: | 
|
Hi allerseits

Aufgabe LF 427.
Diese Aufgabe ist ein Pendant zur Aufgabe LF 426.
Es soll ein Kegelschnitt (KS) aus zwei Tangenten
und drei Punkten konstruiert werden, indem man
den gesuchten KS als kollineares Bild eines geeigneten
Kreises auffasst.
Daten:
Der KS soll die beiden Koordinatenachsen berühren
und durch die Punkte P1(3/4) , P2(4/3) , P3(6/6) gehen.
Aus einer genauen Zeichnung sollen die Koordinaten
der Beruehrungspunkte auf den Koordinatenachsen
ermittelt werden; sufficit.
Anmerkung
Es genuegt, nur eine moegliche Loesung zu beruecksichtigen.
ein Loesungshinweis mit guten Ratschlaegen folgt.
MfG
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4202
Registriert: 07-2002
| | Veröffentlicht am Dienstag, den 22. Juni, 2004 - 14:18: | 
|
Hi allerseits

Hier die versprochene Lösungshilfe.
Ich habe die Methode bei den Druiden gelernt und gebe sie nicht
gerne preis;gleichwohl:
Der zum gesuchten KS zentralkollineare Kreis k beliebiger Grösse
wird durch die gegebenen Punkte P1 und P2 gelegt.´
Die Punkte und Geraden im Kreissystem erhalten Striche,
diejenigen Elemente,welche zum KS-System gehören,
sind ungestrichen.
Die Verbindungsgerade der Punkte P1 P2 wird zur
Kollineationsachse e = e´.
Die x-Achse als Tangente des KS schneidet e in A,
die y-Achse als weitere Tangente des KS schneidet e in B.
Lege durch A eine Kreistangente x´ (zwei Möglichkeiten),
Berührungspunkt X´ mit k.
Tue dasselbe mit y´ von B aus, Berührungspunkt mit k: Y´.
´
Ziel:Konstruktion der Punkte X auf der x-Achse,Y aud der y-Achse.
Man suche und finde durch intensives Nachdenken:
1.
Den korrspondierenden Punkt S´ zum Schnittpunkt S = O
der Tangenten x und y.
2.
den korrespondierenden Punkt P3´ zu P3.
Man bestimme zum krönenden Abschluss die zur Geraden
h ´ = P3´ X´ korrespondierende Gerade h = P3 X
Beachte,dass h und h´ sich auf der Kollineationsachse e schneiden.
Man bezeichne diesen Schnittpunkt mit E.
Anmerkung
Man zeichne auf einem A4-Blatt, Einheit 1 cm, O in der Mitte des Blattes.
Kreis k: Mittelpunkt M(1/1).
Ich werde die Näherungswerte der Koordinaten wesentlicher
Punkte später angeben.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4203
Registriert: 07-2002
| | Veröffentlicht am Dienstag, den 22. Juni, 2004 - 16:06: | 
|
Hi allerseits

Hier die Daten wesentlicher Elemente der Konstruktion.
A(7/0),B(0/7).
Kollineationsachse e´= e = AB: x + y = 7
P1=P1´ ; P2 = P2´
Kreis: k (x-1)^2 + (y-1)^2 = 13
Kreistangente x´ durch A , Berührpunkt X´(2,63/-2,22),
Kreistangente y´ durch B , Berührpunkt Y´(-2,22/2,63)
P3´ (-1,55/-1,55) auf k und y = x.
S´ als Schnittpunkt von x´,y´: S´(-7,23 / -7,23).
h´ = P3´´X´schneidet e in E (10,47/-3,47)
Schlussresultat X(8,83/0) auf h = E P3.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1457
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 22. Juni, 2004 - 21:57: | 
|
Hi megamath,
leider komme ich erst jetzt zu der Konstruktion: ich habs mal versucht zu visualisieren! Hoffe es ist nicht zu konfuss wegen der ganzen Geraden, ich habe auch gleich mal Y genau so konstruiert. Ich hätte auch an y = x spiegeln können...
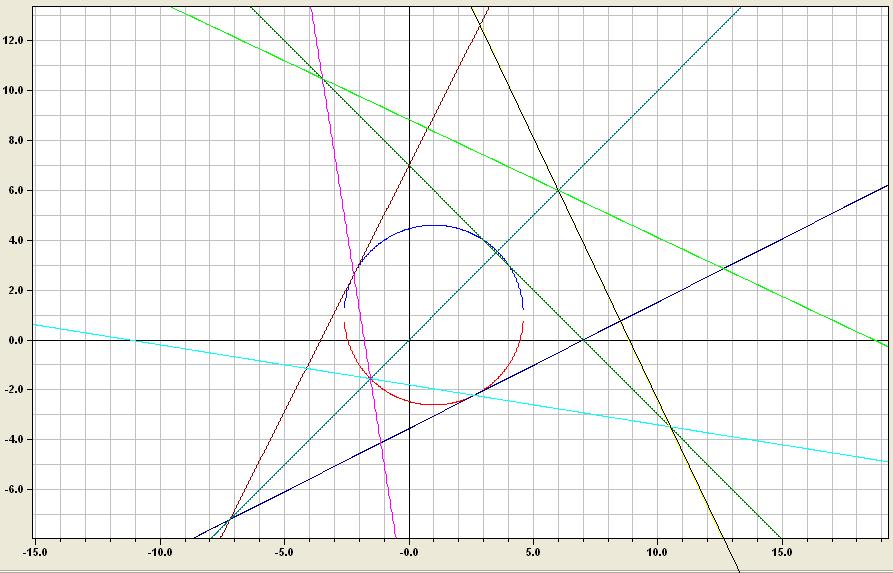
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4204
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 23. Juni, 2004 - 07:47: | 
|
Hi Ferdi

Du hast Dir grosse Mühe gegeben, eine Figur zu erstellen.
Sie ist in allen Teilen richtig.
Die Geraden dürfen und sollen in ihrer ganzen Länge,
soweit es eben geht, gezeichnet werden
und sollen jeweils gegen den Rand hin angeschrieben
werden; dadurch wird alles nicht so konfus.
Ich habe die Figur ausgedruckt und nach meinen früheren Angaben
beschriftet, dies fördert das Verständnis.
Es ist alles ok und alles wird im Nachhinein bei intensiver Betrachtung
verständlich werden.
Nochmals besten Dank!
PS
Beachte, dass man bei der Lösung ganz ohne Kollineatioszentrum Z
zum Ziel gelangt!
Nützliche Übung: man trage Z in der Figur ein.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1459
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 23. Juni, 2004 - 10:54: | 
|
Hi megamath,

ich hatte mich auch schon gefragt, wie es mit dem Zentrum aussieht, aber wie lautet eigentlich die Definition für das Kollineationszentrum?
In der Hyperbelaufgabe LF 425 haben wir einfach den Schnittpunkt der Asymptoten als Zentrum gewählt, dafür kamen wir ohne die Achse aus!
Aber es muss ja einen Zusammenhang geben zwischen der Achse und dem Zentrum! Also ist hier durch die Wahl der Achse das Zentrum wohl schon vorgegeben. Nur wie man es findet ist die Frage! Einen kleinen Hinweis??
mfg
(Beitrag nachträglich am 23., Juni. 2004 von tl198 editiert) |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4207
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 23. Juni, 2004 - 16:22: | 
|
Hi Ferdi

Der Sachverhalt:
Bei der perspektiven Affinitaet sind die Verbindungsgeraden
entsprechender Punkte wie P und P´ parallel und gehen somit
durch einen und denselben unendlich fernen Punkt Z inf.
Bei der perspektiven Kollineation gehen die Verbindungsgeraden
entsprechender Punkte wie P und P´ durch einen festen
endlichen Punkt Z, das Kollineationszentrum Z.
Für beide Abbildungstypen gilt:
entsprechende Geraden wie g und g´ schneiden sich auf einer
festen Geraden e, der Affinitätsachse bzw. Kollineationsachse.
Im vorliegenden Fall findet man Z als Schnittpunkt der
Kollineationsstrahlen P3 P3´und X X´.
MfG
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1466
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 23. Juni, 2004 - 22:12: | 
|
Hi megamath,
zur Vollständigkeit gebe ich dann noch den Wert an:
Z ~ ( -4,925 | -4,925 )
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4211
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 24. Juni, 2004 - 09:40: | 
|
Hi Ferdi

Die Koordinaten des Zentrums Z sind richtig !
Mit bestem Dank
H.R.Moser,megamath |
|