| Autor |
Beitrag |
    
Toxical (Toxical)

Mitglied
Benutzername: Toxical
Nummer des Beitrags: 27
Registriert: 05-2002
| | Veröffentlicht am Montag, den 07. Juni, 2004 - 18:50: | 
|
Hi
Ich suche due Paramterdarstellung einer funktion
x(phi) y(phi); 0°<=phi<=120°
Ich weiß folgende Sachen:
y'(phi)/x'(phi)=tan(60°-phi)
Int(0°,120°,Sqrt((x'(phi))²+(y'(phi))²)dphi)=a
also die länge von 0° bis 120°
auserdem weiss ich die funktionswerte von y(phi) an den stellen 0°, 60° und 120°, und dass y(phi) symmetrisch zu 60° ist.
Kann man durch diese Angaben bereits eine Parameterdarstellung finden, bzw. muss es überhaupt eine geben?
Vielen Dank im Vorraus für eure Hilfe
Ciao
Eckhard |
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 884
Registriert: 11-2001
| | Veröffentlicht am Dienstag, den 08. Juni, 2004 - 09:00: | 
|
Eckhard,
Hinweis:
Wenn wir an Polarkoordinaten (j,r) denken, also
x=r cos j , y = r sin j,
dann ist
tan j = y/x =>
tan(p/3-j) =
[sqrt(3)- tan j]/[1+sqrt(3) tan j]
= (sqrt(3)x-y)/(x+sqrt(3)y).
Somit haben wir die leicht integrierbare (weil exakte)
Differentialgleichung
[x+sqrt(3)y] dx - [sqrt(3)x-y]dy = 0.
Mittels der Bogenlängen-Bedingung lässt sich die
Integrationskonstante festlegen.
mfG Orion
|
    
Toxical (Toxical)

Mitglied
Benutzername: Toxical
Nummer des Beitrags: 29
Registriert: 05-2002
| | Veröffentlicht am Dienstag, den 08. Juni, 2004 - 19:04: | 
|
Hallo Orion,
danke für Deine Antwort. kann das soweit sogar nachvollziehen.
Mit meinem Wissen über exakte Differentialgleichungen- was als das eines Schülers doch recht beschränkt ist - komme ich auf eine Funktion
F(x,y)=x²/2+y²/2+sqrt(3)xy
Die ja nach x bzw y differentiert den einen bzw. den anderen Term ergibt, und so meines Wissens nach eine Lösung der DGL darstellen müsste.
Nur wundere ich mich weil da jetzt überhaupt kein phi mehr vorkommt und ich ja ein y(phi) und ein x(phi) suchte.
Ich sollte vielleicht noch anmerken, dass das phi bei meinem problem nichts mit Polarkoordinaten zu tun hat, sondern rein zufällig so heißt, es könnte auch t oder sonstwie sein. Ich habe nur phi genommen, weil der Parameter der Wälzwinkel eines abgerollten Dreiecks sein soll. Ich hoffe, das hat keine falschen Überlegungen evoziert.
Ich würde mich sehr freuen, falls du mir noch mals weiterhelfen könntest.
Danke
Eckhard |
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 886
Registriert: 11-2001
| | Veröffentlicht am Dienstag, den 08. Juni, 2004 - 20:53: | 
|
Eckhard,
Eine Dgl.
(1) P(x,y) dx + Q(x,y) dy = 0
heisst exakt, wenn es eine Funktion F(x,y) gibt,
sodass
(2) P(x,y) = Fx(x,y) und Q(x,y) = Fy(x,y).
Das ist der Fall, wenn
(3) Py(x,y) = Qx(x,y).
(Die Indices x,y bedeuten hier partielle Ableitung nach
x bzw. y).
Dann lautet die allgemeine Läsung von (1) in impliziter Form
(4) F(x,y) = C.
In unserem Beispiel ist (dummerweise hatte ich die
Differentiale dx,dy vertauscht !)
(5) P = sqrt(3)x - y , Q = - x - sqrt(3)y.
Also ist (3) erfüllt. Wie man leicht sieht, leistet nun
(6) F(x,y) = sqrt(3)(x2 - y2) - 2xy
das Verlangte:
(7) sqrt(3)(x2 - y2) - 2xy = C
ist die allgemeine Lösung der Dgl. (C ist ein Parameter,
die Integrationskonstante) Man kann (7) auch so
schreiben:
(8) (sqrt(3)x + y)(x - sqrt(3)y) = C.
Man sieht, dass die Integralkurven rechtwinklig-gleichseitige Hyperbeln sind. Die Asymptoten sind
(9) y = - sqrt(3)x und y = 1/sqrt(3)*x.
Der ursprüngliche Parameter j spielt keine
Rolle mehr.
Prüfe bis dahin nochmal alles nach .
mfG Orion
|
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 887
Registriert: 11-2001
| | Veröffentlicht am Mittwoch, den 09. Juni, 2004 - 07:24: | 
|
Eckhard,
Nach dem was du schreibst vermute ich, dass
obiger Ansatz mit j = Polarwinkel nicht
die Lösung liefert, welche deinem Problem
des Abrollens eines Dreiecks entspricht. Wie lautet
denn die genaue Aufgabenstellung ?
mfG Orion
|
    
Toxical (Toxical)

Mitglied
Benutzername: Toxical
Nummer des Beitrags: 31
Registriert: 05-2002
| | Veröffentlicht am Mittwoch, den 09. Juni, 2004 - 15:14: | 
|
Orion,
Danke für die ausführliche Antwort. Genau so habe ich das mit der Funktion F(x,y) auch gedacht, habe nur das + und - verwechselt.
Aber phi als Polarkoordinate aufzufassen scheint tatsächlich zum falschen ergebnis zu führen, hat die von mir erhoffte Funktion doch von ihrer optischen Gestalt wenig Ähnlichkeit mit einer Hyperbel
Das Prblem war folgendes.
Ein gleichseitiges Dreieck, Kantenlänge a, soll auf einer gewissen Kurve so abrollen, dass der Schwerpunkt des Dreiecks stets auf einer Höhe bleibt. Diese gewisse Kurve suche ich.
Damit das Dreieck, dass zuerst auf der einen Spitze stand(phi=0°) auf der nächsten Spitze zu stehen kommt, muss es sich um 120° gedreht haben, daher der Definitionsbereich.
Da ie Dreickskante eine Tangente an der Kurve ist, gibt für die Steigung der Kurve, wenn sich das Dreieck um den Winkel phi gedreht hat
tan(60°-phi)=y'/x'
Ausserdem muss meines erachtens nach die Länge der Kurve von 0° bis 120° - falls das Dreieck nicht "rutschen soll" - gerade a sein.
Die Funktionswerte für phi = 0° bzw. 120° =0; für phi=60° erfibt er sich aus der Forderung, dass der Schwerpunkt auf gleicher Hohe bleiben soll.
Ich hab das mal veranschaulicht.
Hoffe, mein problem ist ketzt klarer geworden, Vielen Dank nochmal
und einen schönen Tag
Eckhard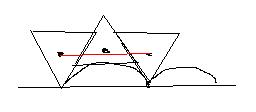 |
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 888
Registriert: 11-2001
| | Veröffentlicht am Mittwoch, den 09. Juni, 2004 - 17:43: | 
|
Eckhard,
Nette Aufghabe ! Leider komme ich heute zu nichts
mehr.
mfG Orion
|
    
Toxical (Toxical)

Mitglied
Benutzername: Toxical
Nummer des Beitrags: 32
Registriert: 05-2002
| | Veröffentlicht am Freitag, den 11. Juni, 2004 - 13:04: | 
|
Ich komme bei der Aufgabe einfach nicht weiter.
Die einzige "verwertbare Aussage" ist doch
tan(Pi/3-phi)=dy/dx
Nur weiß ich leider nicht, wie ich dann weitermache3n bzw. anfangen soll.
Ich danke dir wie immer bereits im Vorraus für Deine Bemühungen.
Eckhard |
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 889
Registriert: 11-2001
| | Veröffentlicht am Freitag, den 11. Juni, 2004 - 16:32: | 
|
Eckhard,
A,B,C seien die Ecken des Dreiecks. Für j=0
sei C im Koordinatenursprung O. Betrachten wir eine
beliebige Zwischenlage, und sei P = (x(j),y(j)) der Berührpunkt der Seite AC mit der Kurve.
Die Abrollbedingung lautet dann m.E.
Für j e d e s j€ [0,2p/3] (also nicht nur für j = 2p/3) gilt
Länge der Strecke CP = Bogenlänge des Kurvenstückes CP .
Diese Bedingung für die Funktionen x(j),y(j) umzusetzen scheint mir schwierig zu sein.
mfG Orion
|
|