| Autor |
Beitrag |
    
Joerdis (Joerdis)

Junior Mitglied
Benutzername: Joerdis
Nummer des Beitrags: 8
Registriert: 01-2004
| | Veröffentlicht am Freitag, den 13. Oktober, 2006 - 21:34: | 
|
Ich brauche dringend hilfe bei ein paar gleichungen und ungleichungen, bei denen ich nicht weiter komme...
a) 1<3^(|x²-x|) < 9 xeR
b) |x+4| < |-x+|x|| xeR
gesucht wird da jeweils x.
bei den anderen beiden gleichungen ist die Frage: Für welche Parameterwerte c bzw a besitzen die Gleichung und die Ungleichung jeweils reelle Lösungen? Bestimmen Sie die Lösung in Abhängigkeit des Parameters.
a) wurzel(x-c+1) + wurzel(x)= 1-c
b) wurzel(2ax-x^2)+wurzel(a^2-x^2) > a
hier habe ich Probleme mit den Summen unter den Wurzeln. Wenn mir jemand helfen könnte wäre das klasse!!! |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 3165
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 14. Oktober, 2006 - 07:34: | 
|
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Polya]
|
    
Elsa13 (Elsa13)

Erfahrenes Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 174
Registriert: 12-2002
| | Veröffentlicht am Samstag, den 14. Oktober, 2006 - 08:04: | 
|
Guten Morgen allerseits,
Fritz hat ein Minus unterschlagen in der Lösung von 1a)  ! !
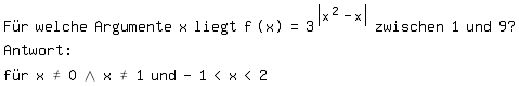
liebe Grüße
elsa |
    
Elsa13 (Elsa13)

Erfahrenes Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 175
Registriert: 12-2002
| | Veröffentlicht am Samstag, den 14. Oktober, 2006 - 08:19: | 
|
Hier noch ein Bildchen zu 1a):
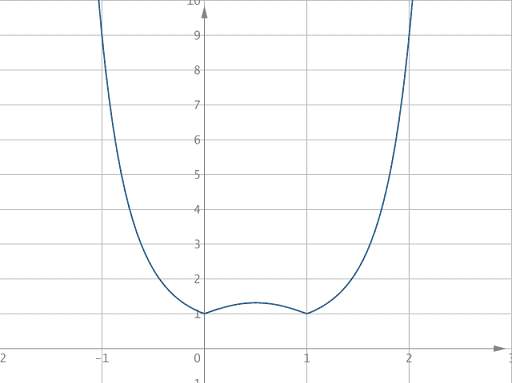 |
    
Elsa13 (Elsa13)

Erfahrenes Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 176
Registriert: 12-2002
| | Veröffentlicht am Samstag, den 14. Oktober, 2006 - 10:13: | 
|
Hi,
die Lösung zu 2b) lautet:
Die Ungleichung gilt für x < -4/3, xeR
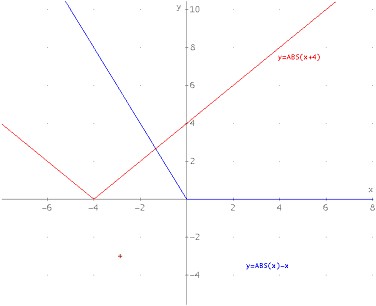
Aus Zeitgründen kann ich im Moment nicht mehr dazu schreiben.
liebe Grüße
elsa |
    
Joerdis (Joerdis)

Junior Mitglied
Benutzername: Joerdis
Nummer des Beitrags: 9
Registriert: 01-2004
| | Veröffentlicht am Samstag, den 14. Oktober, 2006 - 10:30: | 
|
danke!!! 1a und b und 2b sind völlig klar jetzt wo ichs sehe...
könnte mir jemand 2a genau erklären? Ich dachte gestern ich hätte es rausbekommen, aber hab gemerkt, dass ich was übersehen hatte. |
    
Elsa13 (Elsa13)

Erfahrenes Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 177
Registriert: 12-2002
| | Veröffentlicht am Samstag, den 14. Oktober, 2006 - 12:54: | 
|
hallo, Joerdis,
schreibe doch hier herein, wie weit Du bekommen bist! Dann können wir suchen, wo der Fehler liegt.
Es ist ja hauptsächlich Rechnerei, da kann man sich schon irren!
liebe Grüße
elsa |
    
Joerdis (Joerdis)

Junior Mitglied
Benutzername: Joerdis
Nummer des Beitrags: 10
Registriert: 01-2004
| | Veröffentlicht am Samstag, den 14. Oktober, 2006 - 13:13: | 
|
wurzel(x-c+1) + wurzelx = 1-c |²
(x-c+1) +x +2*wurzel((x-c+1)*x)= 1-2c+c²
2*wurzel((x-c+1)*x) = -2x-c+c²
wenn ich jetzt wieder quadriere um die wurzel wegzubekommen, dann wird die rechte seite so kompliziert und führt zu nichts...aber ich weiß nich was ich anderes machen soll. ich muss ja die wurzel irgendwie auflösen um an x zu kommen....
nach der quadrierung steht da:
4x²-4cx+4x= 4x²+4cx-4c²x+c²-2c^3+c^4
zusammengefasst:
0=8cx-4x-4c²x+c²-2c^3+c^4
und dann komm ich nicht weiter... |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 3166
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 14. Oktober, 2006 - 14:39: | 
|
schreib mal u für 1-c, in der 1ten Wurzel und
rechts, und vor dem Quadrieren forme um zu
Wurzel(x+u) = u - wurzel(x)
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Polya]
|
    
Joerdis (Joerdis)

Junior Mitglied
Benutzername: Joerdis
Nummer des Beitrags: 11
Registriert: 01-2004
| | Veröffentlicht am Samstag, den 14. Oktober, 2006 - 16:32: | 
|
suuper danke schön. das hat mir sehr weitergeholfen. |