| Autor |
Beitrag |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4417
Registriert: 07-2002
| | Veröffentlicht am Montag, den 20. September, 2004 - 19:34: | 
|
Hi allerseits

Die folgende Aufgabe 468 ist konstruktiv mit Hilfe
des Satzes von Brianchon zu lösen.
Sie lautet:
Von einer Hyperbel sind die beiden Asymptoten a1 und a2 gegeben sowie eine Tangente t.
Man konstruiere den Berührungspunkt T von t.
Daten:
a1: y = ¾ x
a2: y = - ¾ x
t: 5 x – 4 y = 16.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1604
Registriert: 10-2002
| | Veröffentlicht am Montag, den 20. September, 2004 - 20:38: | 
|
Hi megamath,
auch hier habe ich mir meine Gedanken gemacht!
Sind die Asymptoten wieder als Tangenten mit unendlich fernem Berührpunkt zu sehen?
Ausserdem bin ich mir nicht ganz sicher, ob ich die Tantente t wieder doppelt zählen muss??
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4419
Registriert: 07-2002
| | Veröffentlicht am Dienstag, den 21. September, 2004 - 09:34: | 
|
Hi Ferdi

Deine Überlegungen sind alle richtig!
Die Nummerierung kann z.B. so erfolgen:
Tangente t mit gesuchtem Berührungspunkt T: 6,1;
Asymptote a1: 2,3;
Asymptote a2: 4,5.
Schnittpunkt H = 1,2: H ist ein Punkt im Endlichen.
Schnittpunkt I = 4,5: I ist der unendlich ferne Punkt von a2.
Verbindungsgerade q = HI: q geht durch H und ist zu a2 parallel,
usw.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4420
Registriert: 07-2002
| | Veröffentlicht am Dienstag, den 21. September, 2004 - 09:41: | 
|
Hi allerseits

Die Konfiguration von Brianchon bei der Lösung der vorliegenden
Aufgabe zeitigt ein Nebenresultat.
Bei genauem Hinsehen entdeckt man ein Parallelogramm,
aus dem hervorgeht, dass der Berührungspunkt T die Strecke
auf der Tangente t zwischen den Asymptoten halbiert !
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4421
Registriert: 07-2002
| | Veröffentlicht am Dienstag, den 21. September, 2004 - 09:49: | 
|
Hi Ferdi
  
Um eine frühere Scharte auszuwetzen, kann ich diesmal mit einem
exakten Schlussresultat aufwarten:
die Koordinaten von T sind:
xT = 5, yT = 9 / 4.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1605
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 21. September, 2004 - 15:42: | 
|
Hi megamath,
ich kann dein Eregbniss nur bestätigen...
Hier noch meine Skizze, man erkennt schön das Parallelogramm!
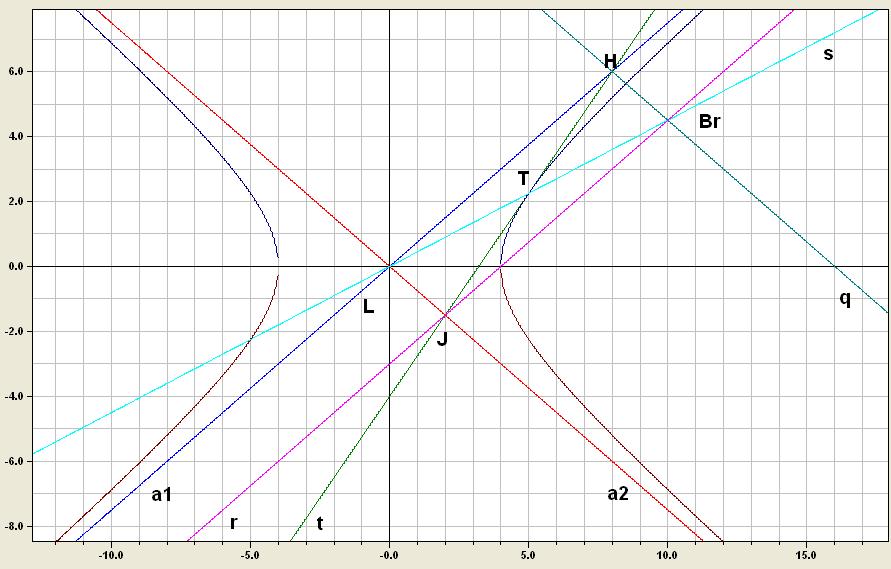
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4422
Registriert: 07-2002
| | Veröffentlicht am Dienstag, den 21. September, 2004 - 16:18: | 
|
Hi Ferdi

Ausgezeichnet!
Besten Dank.
MfG
H.R.Moser,megamath |