| Autor |
Beitrag |
    
Ceagle (Ceagle)

Fortgeschrittenes Mitglied
Benutzername: Ceagle
Nummer des Beitrags: 59
Registriert: 02-2001
| | Veröffentlicht am Montag, den 21. Juni, 2004 - 02:59: | 
|
Hallo,
man kennt die gröbsten Schätzungen zur Anzahl von Primzahlen - beispielsweise ist die Anzahl der Primzahlen zwischen 1 und 2*x weniger als doppeltsohoch als die Anzahl zwischen 1 und x, wodurch man prinzipiell sagen kann, dass der durchschnittliche Anteil an Primzahlen bei größeren x abnimmt.
Nun ist mir, da ich mich recht häufig über alle möglichen Wege und Umwege mit Primzahlen befasse, eine Quasi-Gesetzmäßigkeit bezüglich der Häufigkeit von Primzahlen aufgefallen, die offenbar nur von minimalen Abweichungen begleitet wird, wobei ich jetzt jedoch bei der Beschreibung bei Worten bleibe, da ich persönlich eine gewisse Anschaulichkeit nicht durch mathematische Ausdrucksweise ersetzen möchte.
Betrachtet man einmal die Anzahl der Primzahlen zwischen 1 und int[x * ln(x)] und anschließend die Anzahl zwischen 1 und int[2x * ln(2x)], so ist die Anzahl der Primzahlen in letzterem Fall nahezu verdoppelt - mal sinds ein paar mehr, mal ein paar weniger, der Fehler ist praktisch zu vernachlässigen. Mit int (Integer) ist dabei die Vorkommazahl gemeint - Nachkommastellen werden einfach ignoriert.
int(2,05) = 2
int(3,999999) = 3
int(5,5) = 5
Anbei ein paar Beispiele bezüglich dieser beinahen Prim-Anzahl-Verdopplung, wobei F(x) für int[x*ln(x)] steht.
Bis F(4) = 5 gibt es 3 Primzahlen
Bis F(8) = 16 gibt es 6 Primzahlen (Abweichung 0)
Bis F(16) = 44 gibt es 14 Primzahlen (Abweichung 2, da das Doppelte von 6 eigentlich 12 ist)
Bis F(32) = 110 gibt es 29 Primzahlen (Abweichung 1)
Bis F(64) = 266 gibt es 56 Primzahlen (Abweichung -2)
Bis F(128) = 621 gibt es 114 Primzahlen (Abweichung 2)
Bis F(256) = 1419 gibt es 223 Primzahlen (Abweichung -5)
Bis F(512) = 3194 gibt es 452 Primzahlen (Abweichung 6)
Bis F(1024) = 7097 gibt es 909 Primzahlen (Abweichung 5)
Bis F(2048) = 15615 gibt es 1820 Primzahlen (Abweichung 2)
Bis F(4096) = 34069 gibt es 3644 Primzahlen (Abweichung 4)
Bis F(8192) = 73817 gibt es 7286 Primzahlen (Abweichung -2)
Bis F(16384) = 158991 gibt es 14597 Primzahlen (Abweichung 25)
Bis F(32768) = 340695 gibt es 29239 Primzahlen (Abweichung 45)
Selbiges ist auch bei allen anderen x von F(x) der Fall, wenn man es um einen Faktor n>1 erweitert. Verfünffachen wir es beispielsweise mal, anfangend mit F(3)...
Bis F(3) = 3 gibt es 2 Primzahlen
Bis F(15) = 40 gibt es 12 Primzahlen (Abweichung 2)
Bis F(75) = 323 gibt es 66 Primzahlen (Abweichung 6)
Bis F(375) = 2222 gibt es 331 Primzahlen (Abweichung 1)
Bis F(1875) = 14130 gibt es 1663 Primzahlen (Abweichung 8)
Bis F(9375) = 85741 gibt es 8344 Primzahlen (Abweichung 29)
Bis F(46875) = 504151 gibt es 41846 Primzahlen (Abweichung 126)
Bis F(234375) = 2897971 gibt es 209968 Primzahlen (Abweichung 738)
Vielleicht kann jemand von ja etwas damit anfangen, es weiter ausführen, die Abweichung (annähernd) berechnen, es für irgendwelche anderen Zwecke verwenden oder was auch immer.
Viele Grüße,
Roberto |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 2286
Registriert: 02-2002
| | Veröffentlicht am Montag, den 21. Juni, 2004 - 08:24: | 
|
Gratuliere, daß Du es selbst bemerkt hast, auch
wenn Du nicht der 1te bist - kann mich an das Buch leider nicht mehr erinnern, in dem ich's gelesen habe. Ich glaube, ist ist sogar schon bewiesen.
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Ceagle (Ceagle)

Erfahrenes Mitglied
Benutzername: Ceagle
Nummer des Beitrags: 60
Registriert: 02-2001
| | Veröffentlicht am Montag, den 21. Juni, 2004 - 13:32: | 
|
Hallo Herr Laher,
x * ln(x) soll eigentlich im Schnitt die x-te Primzahl angeben - gut, das ist verdammt ungenau, wie ich finde, genauso wie x / ln(x) zur Angabe der Anzahl der Primzahlen meiner Meinung nach unbrauchbar (wenn auch grundlegend) ist. Daher muss man das ja irgendwie anders missbrauchen können, so dass mir irgendwann das aus meinem ersten Posting in diesem Thread aufgefallen ist.
Kurz mal Themawechsel zu einem anderen Primzahlenthema: wenn man eine Formel zur Annäherung der Anzahl von Primzahlen zwischen 1 und n haben möchte, sollte man möglichst gut zumindest den Durchschnitt der Schwankungen der Primzahlen simulieren können. Nun habe ich das bislang über ein paar Umwege gelöst, um zu recht akkuraten Ergebnissen zu kommen, die zumindest bei den ersten 50-100 Primzahlen fast exakt zutreffen - aber ist irgendeine Möglichkeit bekannt, das ganze irgendwie grundlegend anzugehen, also die Primzahlschwankungen nicht nur billig nachzustellen, sondern über irgendeinen Weg zu simulieren?
Mir gehts dabei weniger darum, eine Durchschnittskurve zu haben, wie es bei der von Riemann vorgeschlagenen Näherung, welche die Zetafunktion enthält, der Fall ist, sondern tatsächlich um das Nachstellen der Primzahlschwankungen, so dass in einem Graphen an möglichst vielen Stellen, an welchen sich Primzahlen befinden, die Näherungskurve um etwa 1 ansteigt. Bisher bin ich dazu bei folgender Formel mit Summenzeichen angelangt, welche mit einer Schrittweite von 0.25 arbeitet.
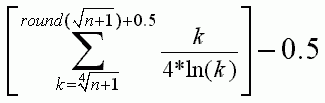
Hierbei wird die Rundung verwendet, um möglichst viele Primzahlen zu "treffen".
Viele Grüße,
Roberto
(Beitrag nachträglich am 21., Juni. 2004 von ceagle editiert) |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 2287
Registriert: 02-2002
| | Veröffentlicht am Montag, den 21. Juni, 2004 - 15:22: | 
|
Tut mir leid wenn ich Dir Hoffnung machte, aber mehr KANN ich nicht sagen
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
|