| Autor |
Beitrag |
    
Malloccalloc (Malloccalloc)

Neues Mitglied
Benutzername: Malloccalloc
Nummer des Beitrags: 1
Registriert: 02-2004
| | Veröffentlicht am Montag, den 23. Februar, 2004 - 18:09: | 
|
Hallo,
ich habe bei einer Aufgabe ein Problem. Ich bekomme einfach nicht den Wert folgender Aufgabe heraus.
Das allgemeine Glied der Reihe lautet:
an = 1/(k² - 1), der Summationsindex k geht von n = 2 bis unendlich.
Wie kann die Summe berechnet werden?
Ich bin Euch wirklich für Hilfe dankbar.
MFG
Dennis
Ich habe mir die anderen Posting mal angeschaut und bin auch schon weitergekommen dadurch. Allerdings scheiter es bei mir wenn ich die Partialbrüche erstellt habe... dann weiss ich nicht weiter.
|
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 796
Registriert: 11-2001
| | Veröffentlicht am Montag, den 23. Februar, 2004 - 18:43: | 
|
Malloccalloc,
Schreibe
ak=(1/2)[1/(k-1)-1/k] + (1/2)[1/k-1/(k+1)]
Dann wird
Sn k=2 ak = (1/2)(1-1/n) + (1/2)[1/2 - 1/(n+1)]
mfG Orion
|
    
Malloccalloc (Malloccalloc)

Neues Mitglied
Benutzername: Malloccalloc
Nummer des Beitrags: 2
Registriert: 02-2004
| | Veröffentlicht am Montag, den 23. Februar, 2004 - 20:05: | 
|
mhhh Orion, damit komme ich irgendwie nicht klar....
ich dachte ich hätte das Prinzip verstanden, aber leider nicht. Ich habe mal die Rechnung als Grafik angehängt. Wäre jemand so nett und kann mir die nächsten Rechenschritte erklären? Das wäre echt super nett 
MFG
Dennis
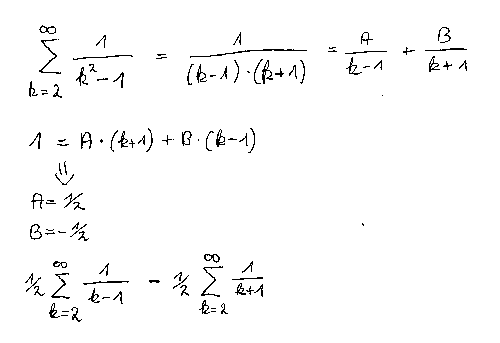 |
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 797
Registriert: 11-2001
| | Veröffentlicht am Montag, den 23. Februar, 2004 - 21:43: | 
|
Malloccalloc,
Die erste Zeile deiner Rechnung macht nur Sinn, wenn
links das Summenzeichen gestrichen wird.
Die beiden Reihen in dener letzten Formelzeile sind
divergent , die beabsichtigte Zerlegung der Reihe als
Differenz von 2 Reihen ist also unzulässig !
Man muss vielmehr zunächst die (endlichen) Partialsummen
sn = Sn k=2 ak
betrachten. Um letztere explizit ausrechnen zu können,
schreiben wir ak wie oben angegeben (es wurde nach erfolgter Partialbruchzerlegung 1/k subtrahiert und gleichzeitig addiert, rechne nach !). Dann entstehen die beiden "Teleskopsummen"
(1/2)Sn k=2 [1/(k-1)-1/k] = (1/2)(1-1/n)
und
(1/2)Sn k=2[1/k-1/(k+1)] = (1/2)[1/2-1/(n+1)]
Es heben sich nämlich alle Summanden ausser dem
ersten und dem letzten weg. (Um das einzusehen
empfehle ich, alles explizit ohne Summenzeichen
aufzuschreiben !). Es handelt sich hierbei um einen
oft angewandten Kunstgriff.
Zum Schluss muss man noch n ®¥ gehen
lassen, und es ergibt sich als Summe der gegebenen
unendlichen Reihe
s = limn®¥ sn = 3/4.
mfG Orion
|
    
Malloccalloc (Malloccalloc)

Neues Mitglied
Benutzername: Malloccalloc
Nummer des Beitrags: 3
Registriert: 02-2004
| | Veröffentlicht am Montag, den 23. Februar, 2004 - 22:25: | 
|
Hallo Orion,
vielen lieben Dank für deine Erklärungen! Ich bin ein kleiner Dussel. Ich habe mich vorhin schlicht weg verlesen 
Jetzt habe ich nur noch eine klitze kleine Frage. Du addierst und subtrahierst jeweils 1/k. Mir ist leider noch nicht ganz klar, warum ich das machen muss. Das man das machen kann, weiss ich, aber warum muss ich die Partialbrüche mit 1/k erweitern?
Den Rest der Rechnungen konnte ich, nachdem du mir die Augen geöffnet hattest, sehr gut nachvollziehen! Vielen vielen Dank ich bin ein ganz großen Schritt weiter dank dir.
MFG
Dennis |
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 798
Registriert: 11-2001
| | Veröffentlicht am Dienstag, den 24. Februar, 2004 - 09:04: | 
|
Dennis,
Eine Teleskopsumme hat allgemein die Form
Sb k=a(ck-ck-1) =
ca-ca-1 + ca+1-ca +...+cb-cb-1
= cb-ca-1.
In deinem Fall hat der k-te Summand leider die Form
ck-1-ck+1. Daher der Kunstgriff: addiere und subtrahiere zugleich ck. Dann kann man obige
Formel anwenden.
mfG Orion
|