| Autor |
Beitrag |
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 656
Registriert: 05-2002
| | Veröffentlicht am Sonntag, den 08. Februar, 2004 - 11:56: | 
|
ausgehend von folgendem:
INT sqrt(tan(x)) dx
Maple liefert folgendes:
1/2*(Tan[x])^(1/2)/(Cos[x]*Sin[x])^(1/2)*Cos[x]*2^(1/2)*
ArcCos[Cos[x] - Sin[x]] -
1/2*2^(1/2)*Log[Cos[x] + 2^(1/2)*(Tan[x])^(1/2)*Cos[x] + Sin[x]]
(bereits in Mathematica Syntax umgewandelt)
mit FullSimplify[] der Ableitung liefert Mathematica richtigerweise Sqrt[Tan[x]]
Das Integral sieht bei Mathematica total anders aus, auch da liefert Mathematica richtigerweise bei der Ableitung wieder die Ausgangsfunktion;
Was bedeutet aber das?
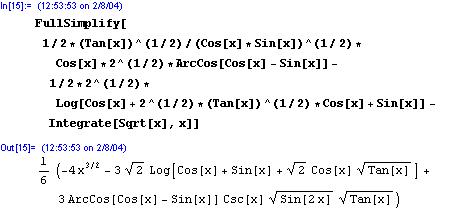
Sollte das nicht eine Konstante sein?
Gruß,
Walter
Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 657
Registriert: 05-2002
| | Veröffentlicht am Sonntag, den 08. Februar, 2004 - 12:09: | 
|

jetzt passt es, ist aber noch ärger 
Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1116
Registriert: 10-2002
| | Veröffentlicht am Sonntag, den 08. Februar, 2004 - 12:18: | 
|
Hi Walter,
ich habe das Integral mal von meinem Mathelehrer bekommen, er fand es in einem Buch mit dem Hinweis: "Bearbeitungszeit : Unendlich"!! Ich hab drei Tage mit der Hand dran gesessen, also ohne PC. Er war überrascht das ich ihm die Richtige Lösung präsentierte!!
Auf Wunsch kann ich später ein wenig von der Monsterrechnung präsentieren!
mfg |
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 658
Registriert: 05-2002
| | Veröffentlicht am Sonntag, den 08. Februar, 2004 - 12:24: | 
|
Hi Ferdi,
ich kenne die Rechnerei von dem Integral, was
mich in dem Zusammenhang aber viel mehr interessiert ist die Tatsache, daß
Maple 8.0 und Mathematica 4.2 unterschiedliche Stammfkt.en bekommen, deren Differenz nicht konstant zu sein scheint.
Ist übrigens mein Lieblingsintegral 
Nur wie interpretiere ich die Differenz?
Gruß,
Walter
Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Niels2 (Niels2)

Senior Mitglied
Benutzername: Niels2
Nummer des Beitrags: 950
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 08. Februar, 2004 - 16:22: | 
|
Hi Ferdi,
mich würde die "Monsterrechnung" mal echt interessieren....
mfg
Niels
|
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 660
Registriert: 05-2002
| | Veröffentlicht am Sonntag, den 08. Februar, 2004 - 17:10: | 
|
http://abakus.hawhaw.de/calc.php <-- ist ein online calculator, der auch den Weg zeigt;
ACHTUNG: der Mathematikminister warnt vor der Verwendung dieses Tools, es kann die Gesundheit beeinträchtigen; 
Viel Spaß Niels

Gruß,
Walter
Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Niels2 (Niels2)

Senior Mitglied
Benutzername: Niels2
Nummer des Beitrags: 952
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 08. Februar, 2004 - 20:32: | 
|
Hi Walter,
das Tool ist echt genial....
vielen Dank für den Link!
mfg
Niels |
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1122
Registriert: 10-2002
| | Veröffentlicht am Sonntag, den 08. Februar, 2004 - 20:35: | 
|
Hi Niels,
hier mein Weg, in drei Schritten damit jeder was davon hat, heute Teil 1 + 2:
ò sqrt(tan(x)) dx
1.)
Sub: sqrt(tan(x)) = t
==> x = arctan(t^2)
==> dx = 2t / ( 1 + t^4 ) dt
====> ò 2t^2 / ( 1 + t^4 ) dt
2.)
Faktoriesieren des Nenners:
1 + t^4 = (1 + at + t^2)(1 + bt + t^2)
1 + t^4 = 1 + (a + b)t + (ab + 2)t^2 + (a + b)t^3 + t^4
==> a + b = 0 und ab + 2 = 0
==> a = sqrt(2) und b = -sqrt(2)
So das wars erstmal für heute, falls erwünscht gehts morgen abend nach der Arbeit weiter mit Teil 3!
mfg |
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1124
Registriert: 10-2002
| | Veröffentlicht am Sonntag, den 08. Februar, 2004 - 20:40: | 
|
Hi Niels,
hier mein Weg, in drei Schritten damit jeder was davon hat, heute Teil 1 + 2:
ò sqrt(tan(x)) dx
1.)
Sub: sqrt(tan(x)) = t
==> x = arctan(t^2)
==> dx = 2t / ( 1 + t^4 ) dt
====> ò 2t^2 / ( 1 + t^4 ) dt
2.)
Faktoriesieren des Nenners:
1 + t^4 = (1 + at + t^2)(1 + bt + t^2)
1 + t^4 = 1 + (a + b)t + (ab + 2)t^2 + (a + b)t^3 + t^4
==> a + b = 0 und ab + 2 = 0
==> a = sqrt(2) und b = -sqrt(2)
So das wars erstmal für heute, falls erwünscht gehts morgen abend nach der Arbeit weiter mit Teil 3!
mfg |
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1127
Registriert: 10-2002
| | Veröffentlicht am Montag, den 09. Februar, 2004 - 20:15: | 
|
Hi,
heute Teil 3:
Partialbruchzerlegung:
2t^2 / (1+t^4) =
(At+b)/(1+sqrt(2)t+t^2) + (Ct+D)/(1-sqrt(2)t+t^2)
Rechte Seite Zähler Ausmultpliziert:
(B+D) + (A+C-sqrt(2)(B-D))t + (sqrt(2)(C-A)+B+D)t^2 + (A+C)t^3
Führt zu:
B+D = 0
(A+C-sqrt(2)(B-D)) = 0
(sqrt(2)(C-A)+B+D) = 2
A+C = 0
Daraus:
B = D = 0 , C = -A = sqrt(2)/2
Voila, morgen bearbeiten wir dann die zwei Integrale!
mfg
|