| Autor |
Beitrag |
    
Panther (panther)

Mitglied
Benutzername: panther
Nummer des Beitrags: 44
Registriert: 04-2003
| | Veröffentlicht am Dienstag, den 17. Juni, 2003 - 19:07: | 
|
Hallo!
Brauche mal wieder eure Hilfe:
Sei a eine zu 10 teilerfremde natürliche Zahl. Man zeige, dass die letzten beiden Ziffern von a2001 und a übereinstimmen. |
    
Xell (vredolf)

Erfahrenes Mitglied
Benutzername: vredolf
Nummer des Beitrags: 125
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 18. Juni, 2003 - 13:01: | 
|
Hi Panther,
1,1,1,1,1,...
2,4,8,6,2,...
3,9,7,1,3,...
4,6,4,6,4,...
5,5,5,5,5,...
6,6,6,6,6,...
7,9,3,1,7,...
8,4,2,6,8,...
9,1,9,1,9,...
^^^^^^
Das sind die Reste von Zahlen mit letzter Ziffer ungleich 0.
Da sich die Reste periodisch wiederholen, sagen wir:
1,5,6 sind 1-zyklisch,
2,3,7,8 sind 4-zyklisch,
4,9 sind 2-zyklisch.
Aus 1|2|4 und 2001=4*500 + 1 folgt die Behauptung.
Gruß,
X.
(Beitrag nachträglich am 18., Juni. 2003 von vredolf editiert) |
    
Xell (vredolf)

Erfahrenes Mitglied
Benutzername: vredolf
Nummer des Beitrags: 127
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 19. Juni, 2003 - 03:51: | 
|
Nachtrag
--------
Meine Argumentation beweist nur die Übereinstimmung der Schlussziffer von a
und der letzten Ziffer von a^2001, NICHT jedoch der letzten
BEIDEN Ziffern beider Zahlen. (Danke für den Hinweis, Friedrich)
Die Aussage ist übrigens falsch, weil 22^2001==72 mod 100. (Win-Taschenrechner -
reicht das als gültiger Beweis? *g*)
(Beitrag nachträglich am 19., Juni. 2003 von vredolf editiert) |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 1239
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 19. Juni, 2003 - 09:01: | 
|
moment, 22 ist nicht Teilerfremd zu 10
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 1240
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 19. Juni, 2003 - 09:37: | 
|
vielleicht hilft das weiter:
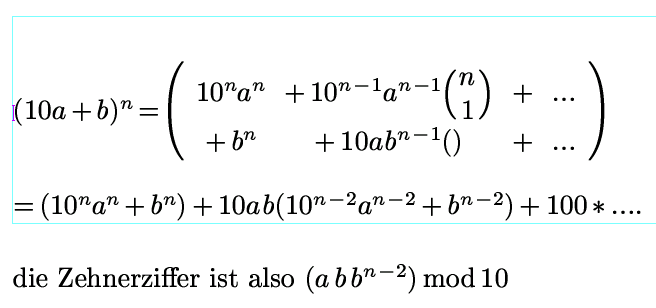
hoppla, ... 10*a*b*n*( .... )
(
den Binomialkoeffizienten hatte ich vergessen
)
die Zehnerziffer ist also
( n*a*b^(n-1) ) mod 10
(Beitrag nachträglich am 19., Juni. 2003 von friedrichlaher editiert)
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
*** (hydra)

Neues Mitglied
Benutzername: hydra
Nummer des Beitrags: 3
Registriert: 06-2003
| | Veröffentlicht am Donnerstag, den 19. Juni, 2003 - 11:49: | 
|
@Panther
ggT(a,10)=1 ==> ggT(a,100)=1.
Aus j(100)=40 folgt damit nach Euler a40 = 1 (mod 100) bzw. a2001 = a (mod 100).
Wegen j(1000)=400 gilt sogar, dass die letzten 3 Ziffern von a2001 und a übereinstimmen, wenn ggT(a,10)=1.
***
|
|