| Autor |
Beitrag |
    
Sandra

| | Veröffentlicht am Freitag, den 22. Juni, 2001 - 09:05: | 
|
Hi Casper007 !
Bitte fange bei einer neuen Frage auch eine neue Diskussion an ! Gerade Deine Frage ist ein gutes Beispiel dafür, daß Herleitungen im Archiv zu finden sein sollten, und in dieser Form findet es dann doch niemend.
Zur Aufgabe:
Zunächst solltest Du eine große und ausführliche Skizze zeichnen, in die Du auch alle rechtwinkligen Dreiecke, am besten bunt, einträgst.
Der Tetraeder habe die Seitenlänge a.
Seine Seiten sind gleichseitige Dreiecke, deren Höhe a/2 mal Wurzel 3 beträgt (aus Formelsammlung oder Pythagoras anwenden, Skizze).
Die Fläche der gleichseitigen Dreiecke beträgt dann 1/2 * Grundlinie * Höhe =
A = ½ * a * a/2 * Wurzel 3 = a²/4 * Wurzel 3.
Für die Höhe des Körpers solltest Du in die Skizze eintragen; ein rechtwinkliges Dreieck aus der Höhe des Körpers (Kathete), der Seitenkante (Hypotenuse) und 2/3 der Höhe der Seitenfläche (Kathete; das liegt daran, daß im gleichseitigen Dreieck die Höhe und die Seitenhalbierenden zusammenfallen und der Schwerpunkt diese Linien im Verhältnis 2:1 teilt).
Die Höhe des Körpers ergibt sich also zu
h² = a² - (2/3 * a/2 * Wurzel 3)²
h² = a² - a²/3
h² = 2/3 a²
h = a * Wurzel (2/3)
Das Volumen des Tetraders errechnet sich dann nach
V = 1/3 Grundfläche mal Höhe (Pyramidenformel), und Du setzt die Werte für Grundfläche und Höhe ein:
V = 1/3 * a²/4 * Wurzel 3 * a * Wurzel 2/3
V = 1/12 * a³ * Wurzel 2
Ich hoffe, ich habe mich nicht verrechnet, aber der Weg stimmt.
Ciao
Sandra |
    
Casper007

| | Veröffentlicht am Sonntag, den 01. Juli, 2001 - 17:06: | 
|
Hallo ihr,
ich muss euch mal wieder um einen mathematischen Rat bitten. Der hat auch etwas mit der vorherigen Frage von mir zu tun.
Aber erst einmal möchte ich mich bei Sandra für die tatkräftige Unterstützung bedanken. Ich hoffe, sie kann mir auch bei dieser Zusatzfrage weiterhelfen.
Frage:
Es geht wieder um eine Formelherleitung, auch von der Pyramide zum Tetraeder.
Den Fläche der Dreiecke beim Tetraeder habe ich, außerdem die Herleitung für Höhe und Volumen.
Was mir nun noch fehlt, ist die Herleitung der Formel für den Mantel (AM) und der Oberflächeninhalt (AO) von der Pyramide zum Tetraeder.
Es wäre toll, wenn jemand diese Antwort kennt!!!
Danke!! |
    
J

| | Veröffentlicht am Montag, den 02. Juli, 2001 - 07:43: | 
|
So ganz versteh ich dein Problem nicht:
ein Tetraeder ist ein sonderfall der Pyramide.
die meisten Leute verstehen unter Tetraeder einen Körper, dessen Flächen 4 kongruente gleichseitige Dreiecke sind.
Wenn du den Flächeninhalt der gleichseitigen Dreicke schon hast, ist die Oberflöche das Vierfache davon und die Mantelfläche das Dreifache.
Wenn du aber schon allgemeine Formeln für Pyramiden hast, bist du bereits fertig, da ein Tetraeder ein Sonderfall der Pyramide ist.
Gruß J |
    
Sandra

| | Veröffentlicht am Montag, den 02. Juli, 2001 - 09:19: | 
|
Hi Casper007 !
J hat schon recht, eigentlich kennst Du ja schon alles. Aber ich lese aus Deiner Frage, daß Du eine direkte Herleitung aus der Pyramidenformel haben willst. Eigentlich brauchst Du dazu kaum zu rechnen, sondern Du müßtest es nur gut "nebeneinanderstellen". Zum Beispiel
Mantelfläche der Pyramide :
AM = n mal Dreiecksfläche, wobei n die Zahl der Ecken der Grundfläche ist
Mantelfläche des Tetraeders:
AM = 3 mal Dreiecksfläche = 3 * a²/4 * Wurzel 3
AM = 3/4 * a² * Wurzel 3
Oberfläche der Pyramide:
Ao = Grundfläche + n mal Dreiecksfläche
Oberfläche des Tetraeders:
Ao = Grundfläche + 3 mal Dreiecksfläche, wobei Grundfläche = Dreiecksfläche
Ao = 4 mal Dreiecksfläche
Ao = 4 * a²/4 * Wurzel 3
Ao = a² * Wurzel 3
Ist es eine solche Herleitung, die Du haben wolltest ?
Ciao
Sandra |
    
Casper007

| | Veröffentlicht am Montag, den 02. Juli, 2001 - 13:33: | 
|
Hi J und Sandra,
es ist toll, dass ihr mir so schnell geantwortet habt, und ich entschuldige mich für die etwas zu allgemein verfasste Frage, aber sie ist nun mal meine Hausaufgabe.
Ich habe die Frage so verstanden, dass wir anhand der im Tafelwerk vorliegenden Formeln (AM, AO, V)von der "allgemeinen" Pyramide - zu den Formeln des Tetraeders kommen sollen (auch AM, AO, V). Denn es besteht ein unmittelbarer Zusammenhang, den ihr richtig erkannt habt, zwischen Pyramide und Tetraeder. Und diese Herleitung der Formeln von Pyramide zum Tetraeder brauche ich.
Sandra war schon auf dem richtigen Weg, als sie die Herleitung vom Volumenen beschrieb. Das gleiche Prinzip müsste man auf AM und AO versuchen anzuwenden.
Die von Sandra aufgestellte Formelherleitung klinkt gut, aber vielleicht gibt es eine weitere Formelherleitung.
Wenn es bei diesen beiden Größen (AM, AO) keinen Zusammmenhang bzw. Formelherleitung gibt, dann geht es eben nicht.
Aber es wäre toll wenn ihr eine weitere Formelherleitung wüsstet.
Gruß Casper007 und
Danke!!! |
    
Sandra

| | Veröffentlicht am Dienstag, den 03. Juli, 2001 - 07:25: | 
|
Hi Casper007 !
Ich versuche es noch einmal etwas genauer, der Gedanke ist allerdings der gleiche wie in meiner letzten Herleitung:
Mantelfläche:
Pyramide: AM = n * Seitenfläche = n * ½ * Grundlinie * Seitenhöhe
für den Tetraeder setzt Du ein:
n = 3 (Zahl der Seitenflächen)
Grundlinie = a (Seitenkante des Tetraeders)
Seitenhöhe = a/2 * Wurzel 3 (schon hergeleitet)
damit ergibt sich:
AM = 3 * ½ * a * a/2 * Wurzel 3 = 3/4 * a² * Wurzel 3
Oberfläche:
Pyramide: Ao = Grundfläche + Mantelfläche
für den Tetraeder setzt Du ein:
Grundfläche (Dreieck) = ½ * Grundlinie * Seitenhöhe
Mantelfläche von oben übernehmen
damit ergibt sich:
Ao = ½ * a * a/2 * Wurzel 3 + 3/4 * a² * Wurzel 3
Ao = ¼ * a² * Wurzel 3 + ¾ * a² * Wurzel 3
Ao = (1/4 + ¾) * a² * Wurzel 3
Ao = a² * Wurzel 3
Mehr fällt mir leider nicht ein. Es kann sein, daß in Deinem Tafelwerk die Formeln der Pyramide etwas anders formuliert sind, aber natürlich müssen sie den gleichen Sinn ergeben. Dann müßtest Du vielleicht noch etwas umformulieren.
Ciao
Sandra |
    
Casper007

| | Veröffentlicht am Sonntag, den 22. Juli, 2001 - 17:10: | 
|
Hi Sandra,
habe meine Arbeit endlich wieder zurück bekommen. Die Herleitung für den Mantel, für die Oberfläche, für das Volumen und für die Höhe war richtig hergeleitet worden.
Die Herleitung für den Flächeninhalt war auch ok, sie wurde nur etwas ergänzt:
AO=4*a²/4*Wurzel
daraus folgt AO=a² Wurzel3
(4 wurde weggekürtzt)
Das war nur der einzige Makel, ansonsten war alles richtig.
Hiermit bedanke ich mich für deine Hilfe und werde natürlich sicherlich wieder einmal vorbei schauen und auch ggf. einmal anderen helfen. Danke
P.S: kannst mir auch eine E-Mail schreiben |
    
Stefanie

| | Veröffentlicht am Samstag, den 29. September, 2001 - 12:39: | 
|
Hallo Leute!
Wir haben gereade in Mathe so ein Projekt gestartet, wo jeder eine Unterrichtsstunde halten muss. Ich hab das Thema: Körperberechnung von Prismen und Zylinder Deswegen brauche ich jetzt alle möglichen Info`s zu dem Thema. Fall´s jemand mir ein paar Info´s geben kann oder ein paar Internetseiten dazu kennt, wär das ziemlich nett! |
    
Matze (Matze)

| | Veröffentlicht am Samstag, den 29. September, 2001 - 14:41: | 
|
http://www.stud.uni-bayreuth.de/~a6415/stoff.html |
    
Danny

| | Veröffentlicht am Donnerstag, den 08. November, 2001 - 13:24: | 
|
Hallo,
ich könnte etwas Hilfe brauchen, und zwar habe ich Schwierigkeiten Formeln umzustellen z.Bsp.
Das Volumen einer Kugel ist vorgegeben, gesucht wird der Radius und der Oberflächeninhalt. Oder von einem Zylinder ist das Volumen bekannt und das seine Höhe dem Durchmesser entspricht gesucht wird der Radius und der Oberflächeninhalt.
ich bin für jede Hilfe dankbar
PS. In Fragen der Physik und der Luftfahrt stehe ich jederzeit zur Verfügung. |
    
Rudolf Friederich (Ruedi)

| | Veröffentlicht am Donnerstag, den 08. November, 2001 - 15:23: | 
|
Hallo
Kugel:
V = 4pr3/3
3V = 4pr3
r = 3.W(3V/4p)
3.W() bedeutet 3. Wurzel
O = 4pr2
Zylinder:
Kreisfläche ist F = r2p
d = 2r = h
V = r2ph
V = (d/2)2pd
V = d2pd/4
4V = d3p
d = 3.W(4V/p)
r = [3.W(4V/p]/2
O = 2r2p + 2rph
O = 2r2p + 4r2p
O = 6r2p
Gruss Ruedi |
    
schüler aus dem gym

| | Veröffentlicht am Mittwoch, den 09. Januar, 2002 - 11:19: | 
|
hallo wir vom gym in gladbeck dürfen für unseren mathe lehrer aufgaben raussuchen so eine sklaverei helft uns bitte wir sind verzweifelt!!! |
    
schüler aus dem gym

| | Veröffentlicht am Mittwoch, den 09. Januar, 2002 - 11:21: | 
|
ich meine aufgaben zur körperberechnung hi |
    
Filipiak

| | Veröffentlicht am Mittwoch, den 09. Januar, 2002 - 18:10: | 
|
Bitte schaut doch ins Archiv: Eine Menge Aufgaben und Lösungen. |
    
Katrin_braucht_hilfe

Unregistrierter Gast
| | Veröffentlicht am Montag, den 18. März, 2002 - 15:27: | 
|
hi leute
ich brauch da mal drigend eure hilfe!!!
schrieben morgen matheüberprüfung nnd ich brauche die formel von einer pyramide, die NICHT quadratisch ist. die für eine quadratische ist ja: M= 2*a*hs und die die ich suche ist???
danke im vorruas!
greetz katrin |
    
Andi (andreas_)

Junior Mitglied
Benutzername: andreas_
Nummer des Beitrags: 6
Registriert: 03-2002
| | Veröffentlicht am Montag, den 18. März, 2002 - 20:56: | 
|
Hallo Katrin!
Wenn ich das richtig verstehe, brauchst Du die Formel für die Mantelfläche einer rechteckigen Pyramide. Der Mantel besteht aus 4 Dreiecken, wobei jeweils 2 gleich sind.
Das eine Dreieck hat eine Seite a (Länge der Grundfläche) und eine Höhe ha. Die Fläche eines solche Dreiecks ist:
A=(a*ha)/2
Weil wir dieses Dreieck aber zweimal haben, ist die Fläche beider Dreiecke:
A=a*ha
Das andere Dreieck hat eine Seite b (Breite der Grundfläche) und eine Höhe hb. Die Fläche eines solchen Dreiecks ist:
A=(b*hb)/2
Da wir auch dieses Dreieck zweimal haben, ist die Fläche beider Dreiecke:
A=b*hb
Für die Gesamtfläche des Mantels müssen wir alle Flächen zusammenzählen:
M=a*ha+b*hb
Ich hoffe, ich konnte Dir damit helfen.
Liebe Grüße -
Andi |
    
Wilm

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 09. April, 2002 - 16:22: | 
|
brauche hilfe!!
ich plane die Körperberechnung nicht |
    
NKD75

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 09. April, 2002 - 17:17: | 
|
Hallo Wilm,
was planst du denn? |
    
studi

Unregistrierter Gast
| | Veröffentlicht am Montag, den 29. April, 2002 - 14:31: | 
|
Hallo Ihr da draußen!!!
Folgendes Problem:
Wie kann man den "Tetraederinnenwinkel" (109,5°) herleiten??Habe viel darüber gefunden,nur keine Herleitung!
Wäre schön,wenn sich jemand kurzfristig dieses Problems annehmen könnte!! |
    
Friedrich Laher (friedrichlaher)

Erfahrenes Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 237
Registriert: 02-2002
| | Veröffentlicht am Mittwoch, den 01. Mai, 2002 - 14:13: | 
|
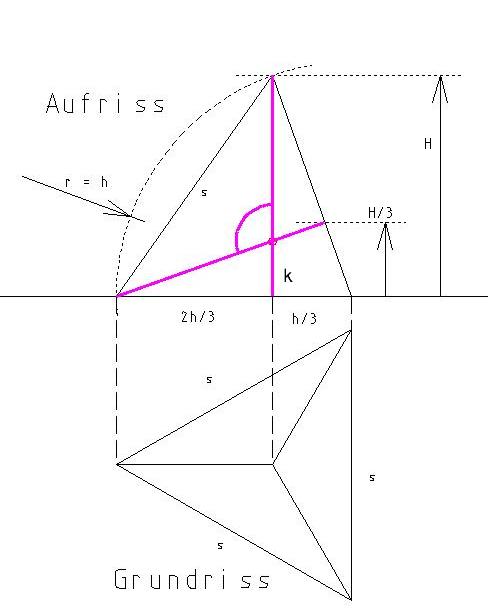
Bezeichnungen:
s = Kantenlänge }
h = Flächenhöhe } des Tetraeders
H = Körperhöher }
Der Winkel den Du meinst ist der zwischen zwei einander schneidenden Höhen H des Tetraeders. Solche sind im Aufriss violett in tatsächlicher Größe und Lage zueinander eingezeichnet.
Der Aufriss ist ein gleichschenkeliges Dreick mit der Basis s und der Schenkellänge h.
Aus dem Bild sollte es Dir möglich sein die Lage des Schnittpunktes der beiden Höhen, also z.B. die Länge k des kürzeren Abschnitts, zu berechnen.
Dann
ist,
z.B., (2h/3)/k der Tangens des Winkels
zwischen
einem k-Abscnitt und dem längerem Abschnitt.
Von
diesem Wert bestimme nun mit dem Taschenrechner
den
Arcustangens (wahrscheinlich eine Taste tan-1 oder Funktion inv tan
oder ähnliches.Subtrahiere von 180° diesen Wert und Du solltest die 109,...° erhalten.
 |
    
kurzvormabi

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 09. Juni, 2002 - 17:37: | 
|
HILFE!
Ich hab diese Woche mein mündliches Abi in Mathe und muss unbedingt ne Frage beantwortet haben!
"Wie gehen sie vor, um bei einer gegebenen wahrscheinlichkeitsevrteilung einer Zufallsvariablen zu überprüfen ob die Zufallsvariable binomialverteilt ist?"
Bitte bitte bitte beeilt euch |
    
Master

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 09. Juni, 2002 - 17:58: | 
|
Bitte bitte bitte neuen Thread dafür öffnen!!!
Master |
    
kurzvormabi

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 09. Juni, 2002 - 20:41: | 
|
hä? |
    
Master

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 09. Juni, 2002 - 22:30: | 
|
Am Ende eines Threads wird deine Frage kaum bzw. ungerne beantwortet werden.
Geh auf Hausaufgabenboard -> Klasse 12-13 -> Abitur -> Stochastik ->
Dann auf "Neuer Beitrag" klicken
Titel geben (z.B. ´Fragen zur Binomialverteilung´ o.ä.)
Text tippen
Dann wird deine Frage eher gesehen (und lieber beantwortet) wie am Ende eines Threads eines anderen. Okay?
Master
|
    
Gretl

Unregistrierter Gast
| | Veröffentlicht am Montag, den 10. Juni, 2002 - 01:00: | 
|
kurzvormabi, du hast noch nicht viel an Internetforen teilgenommen?
Es ist selbstverständlich, einen neuen Thread aufzumachen, zudem das Thema deiner Frage nichts, aber auch gar nichts, mit "Körperberechnung" zu tun hat...
|
    
Walter H. (mainziman)

Mitglied
Benutzername: mainziman
Nummer des Beitrags: 21
Registriert: 05-2002
| | Veröffentlicht am Montag, den 10. Juni, 2002 - 01:15: | 
|
in der 10ten Klasse zum ABI des hab i mir schon immer gewünscht.
Mainzi Man,
a Mainzelmännchen das gerne weiterhilft
|
    
kurzvormabi

Unregistrierter Gast
| | Veröffentlicht am Montag, den 10. Juni, 2002 - 14:01: | 
|
is ja ok hab's doch selber geschnallt, und ne:hab noch nich an vielen internet-foren teilgenommen, wofür auch?!
trotzdem vielen herzlichen Dank für nüscht! |