| Autor |
Beitrag |
    
Shan22 (Shan22)

Mitglied
Benutzername: Shan22
Nummer des Beitrags: 40
Registriert: 12-2003
| | Veröffentlicht am Mittwoch, den 24. November, 2004 - 20:29: | 
|
Hi!
Bräuchte Hilfe bei folgendem Beweis:
Folgede Folge soll kovergieren:
H_n -ln n=(1+ 1/2+...+1/n)-ln n
Vielleicht kann mir da jmd weiterhelfen.
Danke. |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 2512
Registriert: 02-2002
| | Veröffentlicht am Mittwoch, den 24. November, 2004 - 21:38: | 
|
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Shan22 (Shan22)

Mitglied
Benutzername: Shan22
Nummer des Beitrags: 41
Registriert: 12-2003
| | Veröffentlicht am Donnerstag, den 25. November, 2004 - 10:22: | 
|
danke sehr....
is ja relativ kurz der Beweis, das genügt schon?!
lg |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 2513
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 25. November, 2004 - 12:52: | 
|
ich hoffe schon; vielleicht sollte man noch
ein Skizze mit den graphe 1/x, 1/(x+1) und der
Treppenkurv die die Summanden 1/n darstellt
dazutun ( wobei man leider eine sehr große Strecke
für die Einheit, wenigstens vertikal ) nehmen muß,
um etwas zu sehen.
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 2514
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 25. November, 2004 - 13:37: | 
|
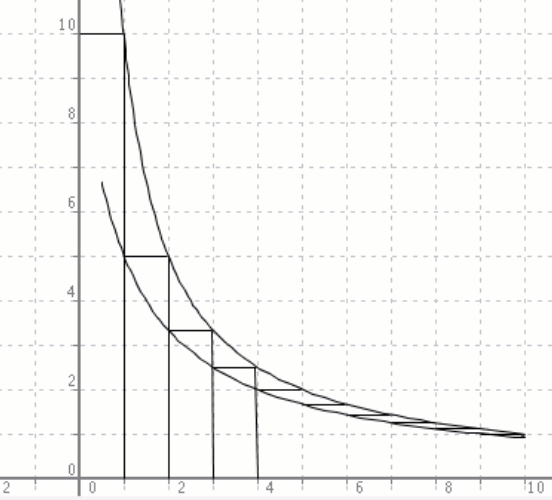
Vertikal: ließ 0.1, 0.2, ... 1 statt 1,2,.. 10
obere Kurve: 1/x, untere 1/(1+x),
Treppe: 1/(1 + [x])
wobei [] die Gaußklammer sein soll,
[x] also die größte ganze Zahl kleiner gleich x
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
|