| Autor |
Beitrag |
    
mathi

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 06. November, 2007 - 20:38: | 
|
Hallo liebe Mathematiker,
ich möchte beweisen dass folgendes a) und b) gleich ist:
a)Das Quadrat der Summer der natürlichen Zahlen von k=1 bis n. (Schreibe es hier aus, da mir ja leider grad kein Summenzeichen zur Verfügung steht).
b) Die Summe der natürlichen Zahlen jeweils potenziert mit 3 von k=1 bis n.
Meine Beweis habe ich mit dem Induktionsanfang angefangen, wo ich gezeigt haben,dass der Sachverhalt für 1 gilt.
Bei der Induktionsvorraussetzung will ich nun zeigen, dass die auch für n gilt, um es schließlich auf n+1 übertragen zu können.
zu a hab ich bei der Induktionsvorraussetzung:
=> (1+n)= 1² +2x1n + n² = 1 +2n+n²
zu b hab ich:
=> 1³ + n³= 1 + n³
Nun will ich erreichen, die beiden letzten Aussagen (1 +n³) und (1+2n+n²) in die gleiche Erscheinungsform zu bringen, sodass offensichtlich ist, dass sie gleich sind.
leider hab ich da grad einen Hänger.
Wer kann mir helfen? |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 3295
Registriert: 02-2002
| | Veröffentlicht am Dienstag, den 06. November, 2007 - 23:11: | 
|
was Du beweisen must ist dass
(n(n+1)/2)² + (n+1)³ = ((n+1)(n+2)/2)²
gilt; links die Induktionsvoraussetzung für k=n,
und der nächste Summand direkt dazu,
rechts, die zu beweisende Formel auf n+1 angewendet
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Polya]
|
    
Mathi

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 07. November, 2007 - 09:52: | 
|
Hallo Friedrichlaher,
ich verstehe nicht ganz, wie man dazu kommt die Formel zu aufzustellen. Kannst du mir das noch genauer erklären?
ich mache sowas zum ersten Mal, deswegen wäre es nett, wenn du so zu sagen das Thema für mich von "null aufwickeln könntest"!
ich verstehe, was du mit Worten unter der Formel beschrieben hast. Das würde ich auch so machen.
Allerdings sieht meine wahrscheinlich falsche Formel dann so aus:
(1+n)³ + ( 1+ (n+1))² =
Teil b) mir n + Teil a) mit (n+1)
So erhalte ich durch Zusammenfassen:
1³ + n³ + (1+n+1)²
=> 1³ + n³ + 2²+ 4n + n²
Um die vollständige Induktion zu beweisen, müsste ich doch aber jetzt wieder
(n+ 1)³ erhalten.
Was ist mein Denkfehler und was mache ich falsch? Es wär nett, wenn ihr mir das ausführlich beschreiben könntet, denn ich habe noch keine Übung darin und kann noch nicht von selbst alles selbstverständlich folgern...
Dankeschön ;0)
Mathi |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 3296
Registriert: 02-2002
| | Veröffentlicht am Mittwoch, den 07. November, 2007 - 10:35: | 
|
Gesucht ist doch die Summe Si=1n i³der 1ten n Kubikzahlen,
beginnen mit 1³
und
zu beweisen ist die Behauptund dass diese gleich dem Quadrat der Summe
G = 1+2+...n ist, und es gilt ja G = n(n+1)/2;
die
Behauptung, als Formel, lautet also
1³+2³+...n³ = (n(n+1)/2)²
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Polya]
|
    
mathi

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 08. November, 2007 - 10:13: | 
|
Hmm, aber ich wäre nie auf diese Formel gekommen. Wie kommt man auf (n(n+1)/2)²? Kann man das logisch herleiten? Ich sehe da gar keine Verbindung zueinander... :-( |
    
mathi

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 08. November, 2007 - 13:09: | 
|
Und wie beweise ich eigentlich, dass die Formel gilt? Durch umformen zu gleichen Termen? Ich versuche das grade und bekomme es nicht hin...
Wer kann mir helfen? |
    
mathi

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 08. November, 2007 - 13:18: | 
|
(n(n+1)/2)² + (n+1)³ = ((n+1)(n+2)/2)²
links kommt bei mir folgendes raus:
n^4/4 + 13/4n² + n³ + 3n +1
und rechts:
n^4/4 + 9/4n² + 1
Leider ist es nicht gleich :0(
Ich bitte um Unterstützung, denn mich interessiert es wirklich |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 3297
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 08. November, 2007 - 13:47: | 
|
links lässt sich (n+1)² "ausklammern", das vereinfacht es
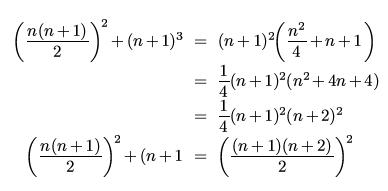
die rechte Seite muss also garnichtmehr ausmultipliziert werden
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Polya]
|
    
Doerrby

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 08. November, 2007 - 18:38: | 
|
Hallo mathi,
vollständige Induktion heißt, dass man
1. eine Behauptung für eine Anfangszahl (hier sinnvollerweise 1) zeigt,
2. folgert, wenn die Behauptung für eine Zahl n gilt, dass sie dann auch für den Nachfolger n+1 gilt.
Dadurch ergibt sich dann, dass die Behauptung ab der Anfangszahl für alle folgenden Zahlen gilt.
Der erste Schritt ist der einfache: Man setzt hier auf beiden Seiten 1 ein und bekommt dasselbe Ergebnis, also gilt die Behauptung für 1.
Den zweiten Schritt hat FriedrichLaher ausführlich beschrieben.
Wie man auf die Formeln kommt, ist für den Beweis egal, aber du kannst dir ja mal eine Excel-Tabelle anlegen: 1. Spalte die Zahlen n, 2. Spalte die Kubikzahlen davon, 3. Spalte die Summen darüber, 4. Spalte die Summen geteilt durch n4 und dann siehst du, dass diese schön langsam nach 1/4 konvergieren. Ziehst du 1/4 n4 von den Summen ab und teilst durch n3, konvergiert's nach 0,5 usw.
So bekommst du am Ende, nach Ausklammern, die Formel 1/4 n2 (n+1)2 .
Gruß Dörrby |
    
mathi

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 08. November, 2007 - 18:38: | 
|
ahh, vielen dank, friedrichlaher! Hast du noch lust mir zu erklären, wie man auf die Terme kommt?
wäre sehr nett ;0) |
    
Doerrby

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 08. November, 2007 - 18:50: | 
|
13 + 23 + ... + n3 + (n+1)3 = ( n*(n+1)/2 )2 + (n+1)3
laut Induktionsvoraussetzung: Du nimmst an, dass die Behauptung für n gilt, deshalb kannst du die Summe bis n3 durch die Formel ersetzen.
Dann hat Friedrichlaher folgende Schritte gemacht:
(n+1)2 ausklammern, 1/4 ausklammern, binomische Formel, Quadrate rausziehen und es steht da:
( (n+1)*(n+1+1)/2 )2 ,
also genau die Formel für n+1 statt für n.
Gruß Dörrby |
    
Doerrby

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 08. November, 2007 - 20:51: | 
|
Natürlich kannst du im 2. Schritt bei
( n*(n+1)/2 )2 + (n+1)3 = ( (n+1)*(n+2)/2 )2
auch beide Seiten ausmultiplizieren und dann beim Koeffizientenvergleich eine Übereinstimmung feststellen, um die Gleichheit zu beweisen. Ich würde hier aber trotzdem 1/4 ausgeklammert lassen. In der Klammer stünde dann:
n4 + 6n3 + 13n2 + 12n + 4
Gruß Dörrby |
|