| Autor |
Beitrag |
    
stacheldino

Unregistrierter Gast
Autor: 217.86.14.98
| | Veröffentlicht am Freitag, den 01. Juli, 2011 - 16:30: | 
|
Einem Halbkreis wird ein Trapez einbeschrieben, dessen eine Grundlinie der Halbkreisdurchmesser ist. Bestimmen Sie den Basiswinkel des Trapezes so, dass der Flächeninhalt des Trapezes möglichst groß wird.
Lösen Sie diese Extremwertaufgabe mit Hilfe der Differentialrechnung!
Dies ist die Aufgabe bei der ich Probleme habe. Wäre euch sehr dankbar wenn mir jemand dabei helfen könnte. 
mfg
Stacheldino |
    
Integralgott (Integralgott)

Junior Mitglied
Benutzername: Integralgott
Nummer des Beitrags: 13
Registriert: 01-2003
| | Veröffentlicht am Samstag, den 21. Januar, 2012 - 15:14: | 
|
Hallo Stacheldino!
Das ist eine schöne Aufgabe. 
Zunächst einmal reduzieren wir die Aufgabenstellung auf einen Viertelkreis, da das Ganze ja symmetrisch ist. In anhängende Skizze habe ich alle Linien eingezeichnet, die wir zum Verständnis benötigen.
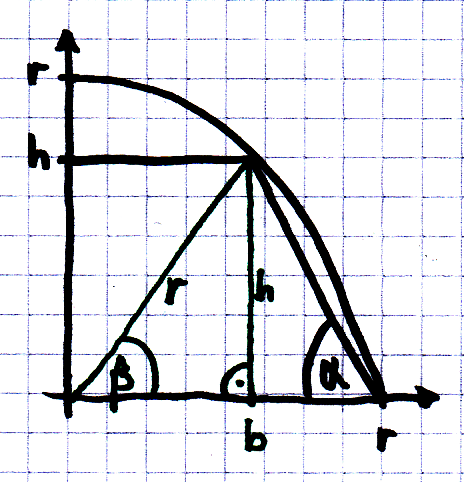
Ganz allgemein suchen wir bei als bekannt vorausgesetztem Radius r zunächst eine Funktion A(alpha), deren Extrempunkt wir dann bestimmen sollen. alpha ist der in der Aufgabenstellung genannte Basiswinkel. Wir ändern die Aufgabe nun ein bisschen:
Durch die Linie vom Ursprung zum Berührungspunkt des halben Trapezes mit dem Viertelkreis ergibt sich ein gleichschenkliges Dreieck mit dem Winkel beta. Die Beziehung zwischen alpha und beta ist festgelegt und lautet nach der Winkelsumme im Dreieck:
(1) beta = 180° - 2*alpha
oder umgestellt nach alpha:
(2) alpha = 90° - (1/2)*beta
Das bedeutet, dass wir die EXTREMALBEDINGUNG auch als Funktion von beta berechnen können, da für ein gefundenes beta ja genau ein korrespondierendes alpha existiert. Wir suchen ein beta zwischen 0° und 90°.
(3) 0° < beta < 90°
Wie aus der Skizze leicht zu entnehmen ist, setzt sich die Fläche des halben Trapezes nun aus einem Rechteck und einem rechtwinkligen Dreieck zusammen:
(4) A(beta) = A{rechteck}(beta) + A{dreieck}(beta)
Die einzelnen Flächenstücke lassen sich zunächst mit den Hilfsgrößen b und h leicht ausdrücken:
(5) A{rechteck} = b*h
(6) A{dreieck} = (1/2)*h*(r-b)
Damit wird die gesamte Fläche
(7) A = (1/2)*h*(b+r)
Leider ist dies noch keine Funktion von beta, da hier noch b und h enthalten sind. Diese müssen wir nun durch die bekannte Größe r und die Variable beta ersetzen. Dies geschieht über folgende NEBENBEDINGUNGEN (vgl. trigonometrische Definitionen am Einheitskreis):
(8) sin(beta) = h/r <=> h = r*sin(beta)
(9) cos(beta) = b/r <=> b = r*cos(beta)
Das in die EXTREMALBEDINGUNG (7) eingesetzt ergibt:
(10) A(beta) = (1/2)*r²*sin(beta)*[1+cos(beta)]
In diesem Ausdruck steht neben dem bekannten Radius r nun nur noch unser Winkel beta als einzige Unbekannte. Wir können nun den Extrempunkt bestimmen.
(Beitrag nachträglich am 21., Januar. 2012 von Integralgott editiert) |
    
Integralgott (Integralgott)

Junior Mitglied
Benutzername: Integralgott
Nummer des Beitrags: 14
Registriert: 01-2003
| | Veröffentlicht am Samstag, den 21. Januar, 2012 - 15:14: | 
|
Die NOTWENDIGE Bedingung zur Bestimmung eines lokalen Extrempunkts ist, dass die Steigung den Wert 0 haben muss (Tangente ist horizontal), daher also die Ableitung verschwindet. Die Ableitung wird hier mit der PRODUKTREGEL bestimmt:
(11) A'(beta) = (1/2)*r²*[cos(beta)*(1+cos(beta)) + sin(beta)*(-sin(beta))]
vereinfacht dann
(12) A'(beta) = (1/2)*r²*[cos(beta) + 2*cos²(beta) - 1]
Damit A'(beta) verschwindet, muss die eckige Klammer 0 werden:
(13) 2*cos²(beta) + cos(beta) - 1 = 0
Damit wir es leicht rechnen können, substituieren wir einfach
(14) cos(beta) = x
und erhalten die einfache quadratische Gleichung:
(15) x² + (1/2)*x - (1/2) = 0
Deren zwei Lösungen sind (p-q-Formel):
(16) x{1} = (1/2) sowie x{2} = -1
Rücksubstituiert mit (14) erhalten wir die Winkel:
(17) beta{1} = 60° sowie beta{2} = 180°
Da nach (3) der gesuchte Winkel durch den Sachverhalt zwischen 0° und 90° liegt, kommt hier nur die erste Lösung in Frage:
(18) beta{max} = 60°
Die HINREICHENDE Bedingung zur Findung eines Extrempunktes benötigen wir ebenfalls nicht, da aus der Geometrie klar wird, dass es sich nur um ein Maximum handeln kann, ein Minimum kommt nicht in Frage. Die Bildung der zweiten Ableitung können wir uns daher sparen. Wenn Du Lust hast, kannst Du es natürlich trotzdem machen (als Übung). 
Wir wissen also nun: Wenn beta 60° hat, dann wird der Flächeninhalt maximal groß. Wir können leicht diesen Flächeninhalt berechnen:
(19) A{max} = (1/2)*r²*sin(60°)*[1+cos(60°)] = [3*sqrt(3)/8]*r²
Dies ist natürlich nur das halbe Trapez, da wir ganz am Anfang ja wegen der Symmetrie nur den Viertelkreis betrachtet haben. Der maximale Flächeninhalt des gesamten Trapezes ist dann:
(20) A{max,trapez} = [3*sqrt(3)/4]*r² ~= 1.299*r²
Die Aufgabe lautete aber ursprünglich, dass die Fläche in Abhängigkeit von alpha maximal groß sein soll. Nach (2) wird:
(21) alpha{max} = 90° - (1/2)*60° = 60°
Der Flächeninhalt des Trapezes wird also maximal, wenn alpha und beta gleich groß, nämlich 60° sind.
Als kleiner Zusatz: Welchen Anteil der Halbkreisfläche nimmt das Trapez nun ein, wenn es maximal groß ist?
(22) p = A{max,trapez}/A{halbkreis}
Mit
(23) A{halbkreis} = (1/2)*PI*r²
wird
(24) p = [3*sqrt(3)]/(2*PI) ~= 0.827 = 82.7%
Viele Grüße,
Integralgott
(Beitrag nachträglich am 21., Januar. 2012 von Integralgott editiert)
(Beitrag nachträglich am 21., Januar. 2012 von Integralgott editiert) |
|