| Autor |
Beitrag |
    
Buffyannes (Buffyannes)

Junior Mitglied
Benutzername: Buffyannes
Nummer des Beitrags: 20
Registriert: 08-2002
| | Veröffentlicht am Donnerstag, den 09. September, 2004 - 20:20: | 
|
Hey leute, hab mal wieder keinen plan.
Habe 3 verschiedene lösungen für die erste ableitung und mit schnittpunkten komm ich auch nicht weiter.
Folgende Aufgabe:
f(x)= (x-1)² : (x+2)
Symmetrie,Achsenschnittpunkte,Ableitungen,Extrema und WP sollen wir bestimmen.
Für symmetrie habe ich herausgefunden
Symmetrie: Punktsymmetrisch
Nullstelle: N1 (0/ 1/2) weiß aber nicht ob das richtig ist.
Könnt ihr mir weiterhelfen was ableitungen angeht und die restlichen Bestimmungen.Brauch das Dringend bis morgen.
Danke leute
MFG
B.  |
    
Sawatzky (Sawatzky)

Erfahrenes Mitglied
Benutzername: Sawatzky
Nummer des Beitrags: 95
Registriert: 01-2002
| | Veröffentlicht am Donnerstag, den 09. September, 2004 - 21:37: | 
|
Hallo B.
doppelt hält besser , was ;-)
ok zur Sache:
3 verschiedene Lösungen für die erste Ableitung ist blöd, da kann man sich schwer entscheiden also schaun wir mal , vielleicht find ich noch ne vierte.
gebrochen rationale Funktion heißt immer ein Auge auf die Definitionslücken werfen. also immer erstmal gucken was rauskommt, wenn man denn Nenner gleich 0 setzt. Mach ich mal
x+2=0
x=-2
sollten wir unterwegs irgendwann mal x=-2 rauskriegen, dann gilt das nicht , weil f(x) für x=-2 nicht definiert ist. schreibt man dann
D(f(x)) = R\-2
aber erst mal die einfachen Sachen (tschuldigung)
zu den achsenschnittpunkten:
schnittpunkte mit der Y-Achse(also x=0)
f(0) = (0-1)^2 : (0+2)=(-1)^2 : 2 = 1/2
SPy=(0/(1/2)) war also richtig bei Dir!!!!!
schnittpunkte mit der x-Achse also f(x)=0
f(x)=0
(x-1)^2 : (x+2)=0 wird genau dann 0 wenn
(x-1)^2=0 also x=1 (doppelte Nullstelle heißt übrigens auch das f'(1)=0)
SPx(1/0)
Symmetrieverhalten bezüglich der Y-Achse oder des Ursprungs(mehr wird eh meist nicht betrachtet)
da gibt es wieder so ein Vorgehensweise, kennste ja schon von mir.
Ich erklär es erstmal:
Symmetrie bezüglich Y-Achse heißt f(x) = f(-x)
also positive und negative x haben immer den gleichen Funktionswert ok?
bei Punktsymmetrie malste Dir am besten mal nen Graph und schaust Dir den nochmal an, denn jetzt kommt ein dicker Hund
Punktsymmetrie bezüglich des Ursprungs heißt -f(x)=f(-x). Also positive und negative x haben immer einen gleichgroßen Funktionswert aber mit jeweils anderem Vorzeichen. (MAL ES DIR AUF)
Da wir ja alle faul sind, ich zumindest ganz doll mach ich das wie folgt ich setze -x ein und schau mir dann an , ob das f(x) oder -f(x) wird oder keins von beiden.
Mach ich dann mal
f(-x)= (-x-1)² : (-x+2)
f(x)= (x-1)² : (x+2) (hmm das ist es nicht)
also f(-x) ungleich f(x) => nicht Y-Achsensymmetrisch
-(f(x))=-(x-1)^2 : (x+2)=(x-1)^2 : (2-x) (das ist es auch nicht)
also f(-x) ungleich -f(x) => nicht punktsymmetrisch bezüglich des Ursprungs
und dann (das find ich selber frech) heißt das keine OFFENSICHTLICHE Symmetrie erkennbar. Da rechnet man sich nen Wolf und dann heißt das nicht OFFENSICHTLICH
ich schieb das schon mal los, Rest kommt gleich
Astrid |
    
Sawatzky (Sawatzky)

Erfahrenes Mitglied
Benutzername: Sawatzky
Nummer des Beitrags: 96
Registriert: 01-2002
| | Veröffentlicht am Donnerstag, den 09. September, 2004 - 22:15: | 
|
hier geht es weiter:
Ableitung gebrochen rationale Funktion, na toll!
Da weiß man wieder warum die gebrochen heißen
ich mach das mal wieder mit nem Schema:
gebrochen rationale Funktionen f(x) haben die Form
f(x)= g(x) : h(x)
bei Deiner
ist g(x) = (x-1)^2 = x^2 -2x+1
und h(x) = (x+2)
die Ableitung von f(x) ist:
(g'(x)*h(x)-g(x)*h'(x)) : (h(x))^2
also brauchen wir g'(x) und h'(x)
g'(x) = 2x-2=2(x-1)
h'(x) = x
jetzt einsetzen:
f'(x)=(g'(x)*h(x)-g(x)*h'(x)) : (h(x))^2
f'(x)=(2(x-1)*(x+2)-((x-1)^2)*x) : (x+2)^2
ausrechnen und zusammenfassen
f'(x)=(2(x^2+2x-x-2)-(x^2 -2x +1)*x): (x+2)^2
f'(x)=(2(x^2+x-2)-(x^3 -2x^2 +x)): (x+2)^2
f'(x)=(2x^2+2x-4-x^3+2x^2-x): (x+2)^2
f'(x)=(-x^3+4x^2+x-4): (x+2)^2
oh mann das wird häßlich
also noch mal gleiches Schema wie oben nur für f'(x)
hier ist
g(x)=(-x^3+4x^2+x-4) und g'(x)=(-3x^2+8x+1)
h(x)=(x+2)^2 und h'(x) = 2(x+2)
f''(x)=((-3x^2+8x+1)*(x+2)^2-(-x^3+4x^2+x-4)*2(x+2)) : ((x+2)^2)^2
f''(x)=((-3x^2+8x+1)*(x+2)^2-(-x^3+4x^2+x-4)*2(x+2)) : (x+2)^4
worauf man sich verlassen kann ist das sich der grad von h immer nur um 1 erhöht also kann ich jetzt auf jeden Fall mit (x+2) kürzen
f''(x)=((-3x^2+8x+1)*(x+2)-(-x^3+4x^2+x-4)*2) : (x+2)^3
häßlich bleibt es trotzdem
f''(x)=(-3x^3+8x^2+x-6x^2+16x+2+2x^3-8x^2-2x+8) : (x+2)^3
f''(x)=(-x^3-6x^2+15x+10) : (x+2)^3
noch mal pack ich heut nicht mehr kannste ja selber mal.
noch ein tip Extrema f'(x) = 0
wir hatten bei f(x)=0 eine doppelte Nullstelle gefunden an x=1 , Du kannst Dich darauf verlassen das dann f'(1) auch 0 ist also das Polynom im Zähler von f'(x) glatt durch (x-1) teilbar ist
dadurch kriegste dann im Zähler von f'(x) eine quadratische Gleichung, die man wieder gut lösen kann.
So ich schau morgen noch mal rein.
Viel Spaß bis dahin
Gruß astrid |
    
Sawatzky (Sawatzky)

Erfahrenes Mitglied
Benutzername: Sawatzky
Nummer des Beitrags: 97
Registriert: 01-2002
| | Veröffentlicht am Donnerstag, den 09. September, 2004 - 22:16: | 
|
noch was rechne meinen Kram auf jeden fall noch mal durch, ich bin schlimm müde
Astrid |
    
Ingo (Ingo)

Moderator
Benutzername: Ingo
Nummer des Beitrags: 970
Registriert: 08-1999
| | Veröffentlicht am Freitag, den 10. September, 2004 - 09:50: | 
|
Kleiner Tip: Manchmal ist es einfacher wenn man gebrochen rationale Funktionen in ein Polynom und eine gebrochen rationaler Funktion zerlegt, deren Nennerfunktion einen niedrigeren Grad hat, als die Zählerfunktion. Hier wäre das der Typ f(x)=(ax+b)+(c/(x+2))
Warum? Ganz einfach: die drei Teilfunktionen lassen sich viel bequemer ableiten.
(x-1)²=x²-2x+1
(x+2)(x-4)=x²+2x-4x-8=x²-2x-8
Also ist f(x)=(x-4)+(9/(x+2)) und somit
f '(x) = 1-9/(x+2)² = ((x+2)²-9)/(x+2) = (x+5)(x-1)/(x+2) [3.Binomi]
f ''(x)= 18/(x+2)³
Es ist direkt ablesbar, daß
f'(x)=0 <=> x=-5 (Maximum wegen f''(-5)<0) oder x=1 (Minimum wegen f''(1)>0)
f ''(x)=0 -> niemals
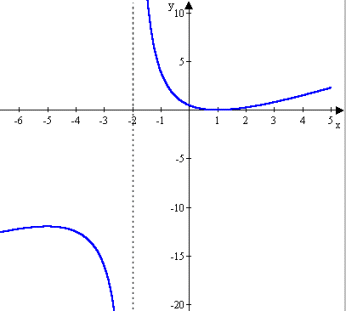
Die eben berechneten Angaben decken sich auch mit dem Schaubild:
 |
|