| Autor |
Beitrag |
    
Istormi (Istormi)

Mitglied
Benutzername: Istormi
Nummer des Beitrags: 48
Registriert: 09-2003
| | Veröffentlicht am Mittwoch, den 09. Juni, 2004 - 16:13: | 
|
Hallo,
hab mal wieder bei nen kleinen Integral ein Problem, vielleicht liegt es aber nur an meinen Anfang.
Mein erster Schritt war u=x^2 zu setzen, womit ich dann auf
0,5*int(1/(1+u^2)*1/(sqrt(u)),x) kam, dass behandelte ich mit der partiellen Integration und kam auf
0,5*arctan(u)/(sqrt(u))+0,25*int(arctan(u)/(sqrt(u)),x)
Aber nu seh ich mit meinen Weg nur Bahnhof
Wie kann ich sonst ran gehen, bitte nur mal um einen Tipp oder zwei.
mfg
Stefan |
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1408
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 09. Juni, 2004 - 16:41: | 
|
Hi,
dieses Integral hat hier einen gewissen Bekanntheitsgrad!
Handelt es sich um unbestimmte Integration?n Oder hat du ein bestimmtes Integral?
Hier hilft nur Partialbruchzerlegung:
x^4 + 1 = (x^2 + 1)^2 - 2x^2
x^4 + 1 = (x^2 + sqrt(2)x + 1)*(x^2 - sqrt(2)x + 1)
Ansatz:
(Ax+B)/(x^2 + sqrt(2)x + 1) + (Cx+D)/(x^2 - sqrt(2)x + 1)
mfg |
    
Istormi (Istormi)

Mitglied
Benutzername: Istormi
Nummer des Beitrags: 49
Registriert: 09-2003
| | Veröffentlicht am Mittwoch, den 09. Juni, 2004 - 17:09: | 
|
Es handelt sich um ein unbestimmtes Integral.
Die Partialbruchzerlegung wollte ich auch zuerst anwenden, doch hab ich es nicht geschafft den Nenner geeignet umzuformen.
Mach jetz mal mit deinen Tipp weiter und meld mich wenn ich´s raus hab oder doch noch weitere Probleme seien sollten.
mfg
Stefan |
    
Istormi (Istormi)

Mitglied
Benutzername: Istormi
Nummer des Beitrags: 50
Registriert: 09-2003
| | Veröffentlicht am Donnerstag, den 10. Juni, 2004 - 13:30: | 
|
Irgend wie krieg ich die Zerlegung nicht gebacken, haben bis jetzt auch nur immer A/(...)+B/(...) genutzt. Sowie die Zerlegung immer mit Hilfe der Nullstellen gemacht, doch hier???
Kannste mal bitte kurz erklären, was man noch so alles über die Partialbruchzerlegung wissen müsste, denn die Methoden der Schule greifen hier nicht. |
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1411
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 10. Juni, 2004 - 21:09: | 
|
Hi,
es ist nicht viel anders!
Wir können den quadratischen Term auch noch zerlegen, dann kommen wir an die vier Nullstellen, nur dann kommen wir auf Komplexe Zahlen etc. Deshalb nimmt man hier mit Vorteil, den Ansatz für quadratische Faktoren!
(Ax+B)/(x^2+sqrt(2)*x+1) + (Cx+D)/(x^2-sqrt(2)*x+1)
Auch hier gilt: auf einen Nenner bringen [(x^4+1)!] und dann Koeffizientenvergleich!
Bei Bedarf kann ich mal ein kleine Zusammenfassung zur Partialbruchzerlgung in einem neuen Thread zusammenschreiben! Das dann aber erst im laufe der Woche!
mfg |
    
Istormi (Istormi)

Fortgeschrittenes Mitglied
Benutzername: Istormi
Nummer des Beitrags: 51
Registriert: 09-2003
| | Veröffentlicht am Freitag, den 11. Juni, 2004 - 14:25: | 
|
Dann werd ich mich mal daran machen
Das wäre super, wenn du mal so eine kleine Zusammenfassung schreiben würdest 
mfg
Stefan |
    
Istormi (Istormi)

Erfahrenes Mitglied
Benutzername: Istormi
Nummer des Beitrags: 52
Registriert: 09-2003
| | Veröffentlicht am Montag, den 14. Juni, 2004 - 12:28: | 
|
Hab jetzt was raus
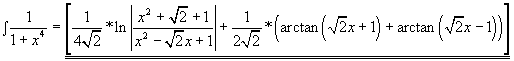 |
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1426
Registriert: 10-2002
| | Veröffentlicht am Montag, den 14. Juni, 2004 - 13:00: | 
|
Hi,
das sieht sehr gut aus! Gratulation. Dieses Integral ist wirklich nicht das einfachste! Das weiß ich aus eigener Erfahrung!
Wenn du Interesse hast, können wir das Ergebniss noch ein wenig verfeinern, indem wir ein Arkustangens-Additionstheorem benutzen! Der letzte Teil deiner Lösung würde dann zu:
1/[2*sqrt(2)] * arctan[ sqrt(2)*x / ( 1 - x^2) ]
mfg |
    
Istormi (Istormi)

Erfahrenes Mitglied
Benutzername: Istormi
Nummer des Beitrags: 53
Registriert: 09-2003
| | Veröffentlicht am Montag, den 14. Juni, 2004 - 15:48: | 
|
Schön , ,
könntest du noch das spezielle Theorem mal angeben, kann ich dann gleich mal zu meiner Sammlung hinzufügen. |
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1428
Registriert: 10-2002
| | Veröffentlicht am Montag, den 14. Juni, 2004 - 22:00: | 
|
Hi,
kein Problem:
Gehen wir vom Tangensadditionstheorem aus:
tan(x+y) = [tan(x) + tan(y)]/[1 - tan(x)*tan(y)]
Setzen wir darin:
x = arctan(u)
y = arctan(v)
tan[arctan(u) + arctan(v)] = [u + v]/[1 - u*v]
oder
arctan(u) + arctan(v) = arctan{[u + v]/[1 - u*v]}
mfg |
    
Istormi (Istormi)

Erfahrenes Mitglied
Benutzername: Istormi
Nummer des Beitrags: 54
Registriert: 09-2003
| | Veröffentlicht am Dienstag, den 15. Juni, 2004 - 08:33: | 
|
Vielen Dank |
    
Istormi (Istormi)

Erfahrenes Mitglied
Benutzername: Istormi
Nummer des Beitrags: 58
Registriert: 09-2003
| | Veröffentlicht am Donnerstag, den 17. Juni, 2004 - 15:49: | 
|
Nu mal noch ne Frage, stimmt die folgende Verallgemeinerung?
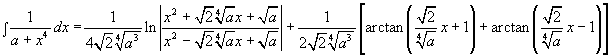
Für a=1 klappt das Ganze, doch für a>1? Wie kann man die Richtigkeit zeigen, außer [F(x)]' zu bestimmen und dann zu vergleichen?
Wegen Faulheit hab ich arctan nicht zusamengefasst;) |
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1436
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 17. Juni, 2004 - 16:04: | 
|
Hi,
dürfte kein Problem darstellen!
Substituiere:
x = a^(1/4) * t
dx = a^(1/4) dt
Einsetzen:
a^(1/4)*int[ 1 / ( a + a*t^4 ) dt ]
Jetzt kannst du das a aus dem Integral ziehen und mit dem a^(1/4) kürzen, es bleibt:
1/a^(3/4) * int[ 1 / ( 1 + t^4 ) dt ]
Am Ende noch rücksubstituieren und der Beweis ist fertig!
mfg |