| Autor |
Beitrag |
    
Sunsyle (Sunsyle)

Mitglied
Benutzername: Sunsyle
Nummer des Beitrags: 17
Registriert: 02-2003
| | Veröffentlicht am Mittwoch, den 25. Februar, 2004 - 19:43: | 
|
damit ich nach dem Muster auch weitere lösen kann!? BITTE
Hier also die Aufgabe:
Gegeben ist die Funktion f(x)=(e^-x)^2. Das Schaubild von f sei K.
a) Führe für die Funktion f eine vollständige Fkt. untersuchung durch.(Wertebereich, Definitionsbereich, nullstellen, grenzwerte, ersten 3 ableitungen extrempunkte und wendepunkte und Grapf zeichnen)
b) ermittle die gleichung der wendetangente.
c)der schnittpunkt von K mit seiner waagerechten Asymptote sei S. Berechne die Koordinaten von S.
d)Das Schaubild K, die waagerechte Asymptote und die Gerade mit der Gleichung x=b (b>0) begrenzen eine Fläche. Berechne ihren Inhalt A(b) sowie lim b-->+ unendlich A(b).
Bitte könnt ihr das mir erlärungen machen damit ich den rechenweg nachvollziehen kann?
Bitte
Danke schonmal
Hab eich Lieb |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 985
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 25. Februar, 2004 - 21:34: | 
|
Für alle, die ev. was dazu schreiben wollen, in der Angabe ist ein Fehler, diese muss heissen:
f(x) = (e^(-x) - 1)²
|
    
Niels2 (Niels2)

Senior Mitglied
Benutzername: Niels2
Nummer des Beitrags: 973
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 26. Februar, 2004 - 10:32: | 
|
Hi Mythos,
du hast vollkommen recht, die in der Aufgabe genannnte Funktion wäre etwas schlecht zu integrieren...hihi...
N. |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 986
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 26. Februar, 2004 - 17:54: | 
|
Hi, ich setz' mal den Graphen rein, einiges haben wir ja schon im Chat besprochen!
Df = R
Wf = R0+
Fortsetzung folgt ev. heute abend noch od. morgen früh!
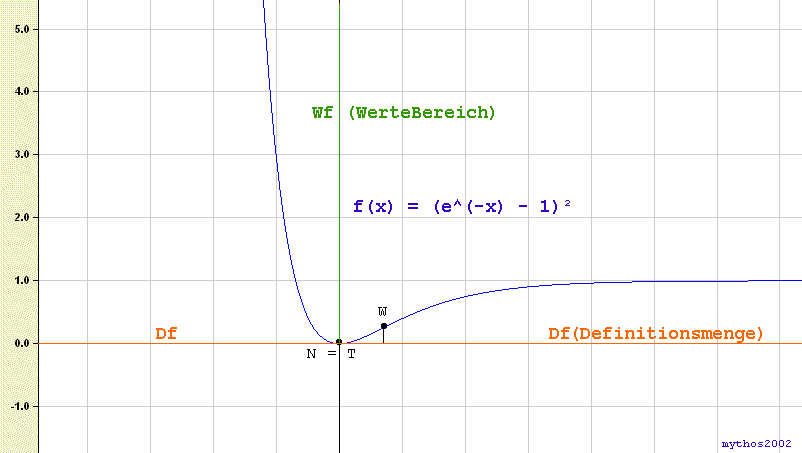
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 989
Registriert: 03-2002
| | Veröffentlicht am Freitag, den 27. Februar, 2004 - 12:20: | 
|
1. Nullstellen:
f(x) = 0
->
(e^(-x) - 1)² = 0, jeden Faktor Null setzen
->
e^(-x) = 1
e^(-x) = e^0
x[1,2] = 0, Doppellösung -> Berührungspunkt N(0|0)
2. Extremstellen:
f '(x) = 0
->
f '(x) = 2*(e^(-x) - 1)*(-e^(-x)) [Kettenregel! -e^(-x) ist die Ableitung von e^(-x), negatives Vorzeichen, weil auch mit der Ableitung von -x zu multiplizieren ist]
f '(x) = -2(e^(-x))*(e^(-x) - 1)
f '(x) = 0, f. Extremum
e^(-x) - 1 = 0
x = 0 (wie oben)
°°°°°
f ''(x) = -2*[-(e^(-x))*(e^(-x) - 1) + (e^(-x))*(-e^(-x))]
(Produktregel, od. vorher ausmultiplizieren)
f ''(x) = 2*e^(-x)*(2*e^(-x) - 1)
x = 0 v. Extremw. einsetzen
f ''(0) = 2 > 0 ->
Minimum T(0|0)
°°°°°°°°°°°°°°°°°°
3. Wendepunkt
f ''(x) = 0
2*e^(-x)*(2*e^(-x) - 1)
2*e^(-x) - 1 = 0
e^(-x) = 1/2 | logaritmieren
-x = -ln(2)
x = ln(2) = 0,69315
y-Wert: f(ln(2)) = (e^(-ln(2)) - 1)² = ((1/2) - 1)² = 1/4
Wendepunkt W(ln(2)|1/4)
°°°°°°°°°°°°°°°°°°°°°°°°°°°°
f '''(x) = 2*[(-e^(-x))*(2*e^(-x) - 1) + e^(-x)*(-e^(-x))]
f '''(x) = -2*e^(-x)*(3*e^(-x) - 1)
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
f '''(ln(2)) muss f. Wendepunkt ungleich Null sein
f '''(ln(2)) = -2*(1/2)*((3/2) - 1) = - 1/2 < > 0 !
Wendetangente:
Steigung ist f '(ln(2))) = -2*(1/2)*((1/2) - 1) = 1/2
Gleichung tw:
y = (1/2)(x - ln(2)) + 1/4
y = x/2 - ln(2)/2 + 1/4
°°°°°°°°°°°°°°°°°°°°°°°°°
od. 2x - 4y - 2*ln(2) + 1 = 0
c) Der Schnittpunkt von K mit seiner waagerechten Asymptote sei S ....
Von wegen! Fangfragen müssen auch sein! Das ist ein Widerspruch in sich, denn eine Asymptote ist ja so definiert, dass die Kurve ihr beliebig nahe kommen kann, ohne sie jedoch jemals zu schneiden oder zu berühren! Daher hat eine Kurve mit ihrer Asymptote im Endlichen nie einen Schnittpunkt.
Wir können jedoch diese (waagrechte) Asymptote berechnen, indem wir den Grenzwert von f(x) für x -> +oo ermitteln:
lim[x -> +oo](e^(-x) - 1)² = 1,
dies, weil lim e^(x) = lim 1/e^x = 1/oo = 0 f. x -> +oo
Asymptote: y = 1
°°°°°°°°°°°°°°°°°°°
lim[x -> -oo](e^(-x) - 1)² = lim[x -> oo](e^(x) - 1)² = oo, also geht der Graph für immer negativere x gegen oo
Fortsetzung folgt!
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 990
Registriert: 03-2002
| | Veröffentlicht am Freitag, den 27. Februar, 2004 - 12:24: | 
|
(Fortsetzung)
d) Das Schaubild K, die waagerechte Asymptote und die Gerade mit der Gleichung x=b (b>0) begrenzen eine Fläche. Berechne ihren Inhalt A(b) sowie lim b-->+ unendlich A(b).
Die Fläche zwischen Asymptote (y = 1) und Kurve K erhält man durch Integration der Differenz der beiden in den Grenzen von 0 (dort berührt K die x-Achse) bis b!
A(b) = int[0;b][1 - (e^(-x) - 1)²]dx
A(b) = int[0;b](1 - e^(-2x) + 2*e^(-x) - 1)dx
A(b) = int[0;b](-e^(-2x) + 2*e^(-x))dx
Gliedweise integrieren, mittels
Subst.:
-2x = u -> dx = -du/2 bzw. beim zweiten
-x = u -> dx = -du
Es sind: int(e^(-2x))dx = -(1/2)e^(-2x) und int(e^(-x))dx = -e^(-x)
A(b) = (1/2)*e^(-2x)[0;b] - 2*e^(-x)[0;b]
A(b) = (1/2)*[e^(-2b) - 1] - 2*e^(-b) + 2
A(b) = (1/2)*e^(-2b) - 2*e^(-b) + 3/2
A(b) = 1/(2*e^(2b)) - 2/e^(b) + 3/2
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Für b -> +oo ist
A = lim[b -> oo] A(b) = 3/2
die Nenner der ersten beiden Brüche gehen gegen -> oo, daher werden die Brüche 0
A = 3/2 FE
°°°°°°°°°°°
Und dazu noch den entsprechend ergänzten Graphen ...
Exp(-x)2b.gif
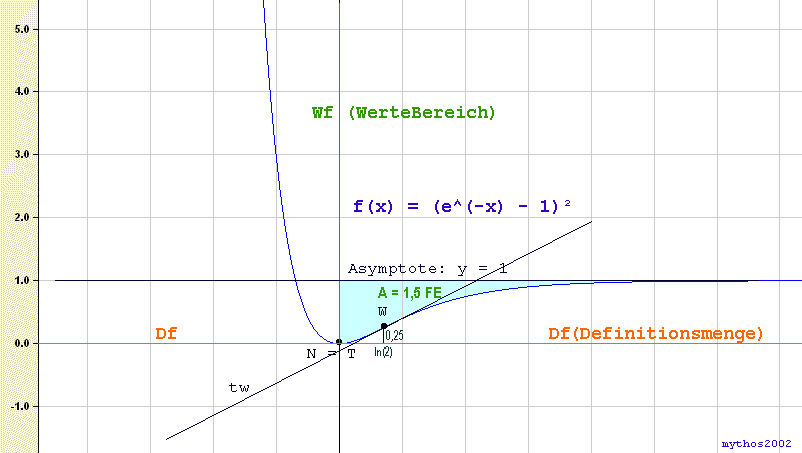
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 991
Registriert: 03-2002
| | Veröffentlicht am Samstag, den 28. Februar, 2004 - 13:10: | 
|
Hallo nochmal,
man sollte sich die Angabe doch genau durchlesen! Leider habe ich übersehen, dass dies mit der Asymptote doch keine Fangfrage war, denn auf der linken Seite existiert ja wirklich ein Schnittpunkt (S) mit der Asymptote, wie es ja auch in der Grafik zu sehen ist!
Wir berechnen also S, indem wir die beiden Gleichungen
y = (e^(-x) - 1)²
y = 1
-------------------
gleichsetzen und nach x auflösen:
e^(-2x) - 2*e^(-x) + 1 = 1
e^(-2x) - 2*e^(-x) = 0
setze e^(-x) = z
z² - 2z = 0
z*(z - 2) = 0
z1 = 0; z2 = 2
rückeinsetzen
e^(-x) = 0 -> keine Lösung
e^(-x) = 2 | ln
-x = ln(2)
->
x = -ln(2); y = 1; -> S(-ln(2)|1)
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Daher ist bei der gesuchten Fläche bei der unteren Grenze statt 0 eben -ln(2) zu nehmen, aber es ändert sich nicht gar so viel, der Weg bleibt vollkommen gleich:
Bitte ab hier entsprechend wie folgt korrigieren:
...
Die Fläche zwischen Asymptote (y = 1) und Kurve K erhält man durch Integration der Differenz der beiden in den Grenzen von -ln(2) (dort schneidet K die Asymptote) bis b!
A(b) = int[-ln(2);b][1 - (e^(-x) - 1)²]dx
A(b) = int[-ln(2);b](1 - e^(-2x) + 2*e^(-x) - 1)dx
A(b) = int[-ln(2);b](-e^(-2x) + 2*e^(-x))dx
Gliedweise integrieren, mittels
Subst.:
-2x = u -> dx = -du/2 bzw. beim zweiten
-x = u -> dx = -du
Es sind: int(e^(-2x))dx = -(1/2)e^(-2x) und int(e^(-x))dx = -e^(-x)
A(b) = (1/2)*e^(-2x)[-ln(2);b] - 2*e^(-x)[-ln(2);b]
Beim Einsetzen der unteren Grenze wird e^(-x) zu 2 und e^(-2x) zu 4
A(b) = (1/2)*[e^(-2b) - 4] - 2*e^(-b) + 4
A(b) = (1/2)*e^(-2b) - 2*e^(-b) + 2
A(b) = 1/(2*e^(2b)) - 2/e^(b) + 2
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Für b -> +oo ist
A = lim[b -> oo] A(b) = 2
die Nenner der ersten beiden Brüche gehen gegen -> oo, daher werden die Brüche 0
A = 2 FE
°°°°°°°°°
Also gehört in der Skizze der linke kleine Teil der Fläche bis zum Schnittpunkt S ebenfalls dazu und grün ausgefüllt, und die Gesamtfläche ist daher 2 FE.
Es läßt sich leider kein Bild mehr hochladen! Was sagt die Technik dazu?
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 993
Registriert: 03-2002
| | Veröffentlicht am Samstag, den 28. Februar, 2004 - 15:11: | 
|
Jetzt geht es!
D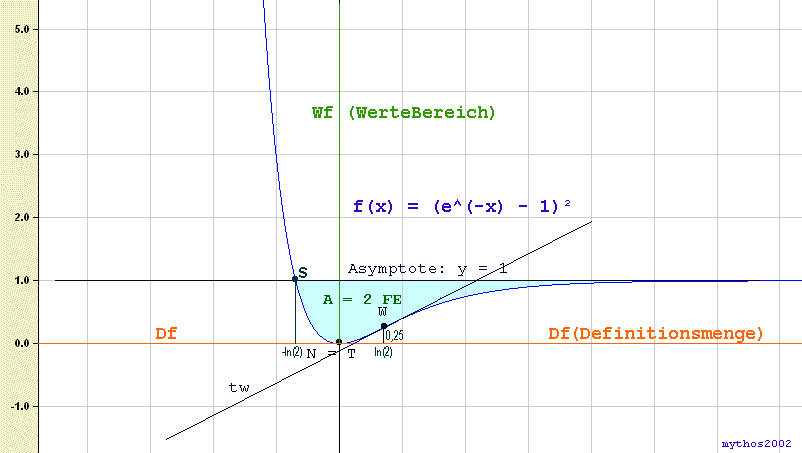 |
    
Sunsyle (Sunsyle)

Mitglied
Benutzername: Sunsyle
Nummer des Beitrags: 18
Registriert: 02-2003
| | Veröffentlicht am Samstag, den 28. Februar, 2004 - 18:49: | 
|
vieln dank nochmal war ttal lieb!
Bis bald
|
|