| Autor |
Beitrag |
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 64
Registriert: 09-2003
| | Veröffentlicht am Donnerstag, den 15. Januar, 2004 - 16:48: | 
|
f(x) = 1/((x+1)*ln(x+1))
mit der größtmöglichen Definitionsmenge Df. Der Graph von f wird mit Gf bezeichnet.
Hinweis: lim x-->0 (x*lnx) = 0 darf ohne Beweis verwendet werden.
1.)
a) Bestimmen Sie Df und untersuchen Sie das Verhalten von f an den Rändern von Df. Geben Sie auch alle Asymptoten an.
b) bestätigen Sie f´(x)= - (1+ln(x+1)) / ((x+1)*ln(x+1))^2
Ermittlen Sie das Monotonierverhalten von f sowie Art und Lage des Extrempunktes.
c) Geben Sie die Gleichung der Tangente t im Punkt (e^-1/ 1/e)) an.
Fortsetzung folgt...
|
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 65
Registriert: 09-2003
| | Veröffentlicht am Donnerstag, den 15. Januar, 2004 - 16:52: | 
|
2.)
a) Begründen Sie allgemein, dass jede strenge monotone Funktion umkehrbar ist. Zeigen Sie durch Angabe eines Beispiels, dass jedoch nicht jede umkehrbare Funktion streng monoton ist.
b) Die Einschränkung f* von f auf D* = R+ ist umkehrbar. Für die Umkehrfunktion g von f* lässt sich kein Funktionsterm g(x) angeben. Geben Sie trotzdem g(1/e) undf g´(1/e) an.
|
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 66
Registriert: 09-2003
| | Veröffentlicht am Donnerstag, den 15. Januar, 2004 - 16:57: | 
|
3.) Nun wird für k > 0 die Schar der Intgralfunktion Jk (x) = Integral von k (unten) bis x (oben)f(t) dt betrachtet.
a) Geben Sie die maximale Definitionsmenge Dk von Jk an.
b) Bestimmen Sie eine integralfreie Darstellung von Jk.
c) Es gilt: Je-1(x) = ln(ln(x+1))
Lösen Sie die Gleichung
-Je-1 (sqrt(e-1)= Je-1(x)
nach x auf und deuten Sie Ihr Ergebnis geometrisch.
P.S. e-1 ist der Index bei J
Vielen Dank schon mal für Hilfe!!! |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 881
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 15. Januar, 2004 - 17:23: | 
|
Hallo!
Die Netiqette gebietet es, nicht eine größere Menge von Aufgaben kommentarlos zu posten.
Bitte, es soll kein Mißverständnis entstehen, konstruktive Hilfe soll und wird sicher gerne zuteil werden, aber die 8 Teilaufgaben, die z.T. weite Themengebiete abdecken, schauen doch sehr nach einer Art Hausaufgabenservice aus.
Es wäre gut, wenn du anfangs die Menge der Aufgaben begrenzen und dafür auch deine eigenen Gedanken, Lösungsansätze bzw. Punkte mitteilen könntest, bei denen du Schwierigkeiten hast.
Denn durch das Abitur musst du letztendlich selbstständig kommen, wir sollten lediglich eine begleitende Unterstützung bieten.
Das ist meine bescheidene Meinung, die natürlich von den anderen nicht unbedingt geteilt werden muss.
Gr
mYthos
|
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 67
Registriert: 09-2003
| | Veröffentlicht am Dienstag, den 20. Januar, 2004 - 11:32: | 
|
Ich sehe das hier ganz bestimmt nicht als Hausaufgabenforum!!!!
Ich hab das durchgerechnet und Lösungen gesehen, doch bei einigen Sachen weiß ich überhaupt nicht weiter oder bin mir unsicher...
Wieso ist der Definitionsbereich das offene Intervall von -1 bis oo, mit Ausnahme der Null?? wie kommt man darauf??? Mir ist nur klar, dass Null ausgeschlossen ist, weil sonst der Nenner Null wird, aber der rest???
Verhalten an den rändern hab ich einigermaßen verstanden.
Probleme bereitet mir die Ableitung, denn irgendwie sind bei mir die Vorzeichen anders!
Meine Rechnung (Mit Quotienten und Produktregel):
f´(x)=(0*((x+1)*ln(x+1))-1*(1*ln(x+1)+(x+1)*1/(x+1)*1))/((x+1)*ln(x+1))^2
= -(ln(x+1)+(x+1)/(x+1))/((x+1)*ln(x+1))^2
= -ln(x+1)-1/((x+1)*ln(x+1))^2
Das stimmt aber leider nicht mit dem Ergebnis oben überein!! Kann mir jemand sagen, wo der Fehler liegt???
beim Monotonieverhalten weiß ich nicht weiter...
Kann mir jetzt soweit erst mal BITTE jemand helfen??
mfg, Avril
|
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 75
Registriert: 12-2002
| | Veröffentlicht am Dienstag, den 20. Januar, 2004 - 18:51: | 
|
zu a)Die Nullstellen des Nenners sind nicht in Df enthalten: also (x+1)*ln(x+1)= 0
*Ein Produkt ist null,wenn einer der Faktoren null ist,also:
x+1=0
x=-1
*****
ln(x+1)=0
e^(ln(x+1)=e^0
x+1=1
x=0
*****
Also entfallen schon mal x=0 und x=-1 aus Df.
Der Logarithmus einer Zahl a zur Basis b>0 ist nur definiert,wenn a>0 ist,da ich niemals eine negative Zahl erhalten kann,wenn ich eine positive Zahl mit einer anderen Zahl potenziere.
Weil also a>0 sein muss,muss gelten:
x+1>0
x>-1
*****
(Wiederholung:Die Zahl c bzw. log(b)a ist die Zahl, mit der ich b potenzieren muss, um a zu erhalten: b^c = a)
(Beitrag nachträglich am 20., Januar. 2004 von Kratas editiert) |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 886
Registriert: 03-2002
| | Veröffentlicht am Dienstag, den 20. Januar, 2004 - 18:58: | 
|
Hi Avril,
bei der Funktion f(x) = 1/((x+1)*ln(x+1)) sind zunächst einmal zwei Faktoren im Nenner, welche nicht Null sein dürfen:
x + 1 <> 0 daraus -> x <> -1, und
ln(x + 1) <> 0, daraus -> x + 1 <> 1 [weil nämlich ln(1) = 0] und daraus -> x <> 0
Dann gilt noch, dass die Logarithmusfunktion ln(x) nur für positive x (ungleich Null) definiert ist, somit muss gelten:
x + 1 > 0, also x > -1
Daraus ergibt sich nun die größtmögliche Definitionsmenge
Df = {x| -1 < x < +oo UND x <> 0}
Dieser Punkt müßte nun klar sein.
(wird fortgesetzt)
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 887
Registriert: 03-2002
| | Veröffentlicht am Dienstag, den 20. Januar, 2004 - 20:13: | 
|
Nun zur Ableitung! Deine Rechnung ist - abgesehen von einer fehlenden Klammer in der letzten Zeile - in allen Schritten vollkommen richtig! Du erhältst:
f '(x) = (-ln(x + 1) - 1)/((x + 1)*ln(x + 1))²
und das ist doch identisch (schau genau!) mit der angegebenen Lösung
f '(x)= - (1 + ln(x + 1))/((x+1)*ln(x+1))²
Das Monotonieverhalten kann durch das Vorzeichen der 1. Ableitung geklärt werden. Allgemein gilt folgendes:
f(x) monoton steigend in einem Intervall [a;b]:
Für alle x aus [a;b] gilt:
f '(x) > 0
f(x) monoton fallend in einem Intervall [a;b]:
Für alle x aus [a;b] gilt:
f '(x) < 0
An einer relativen Extremstelle x_e (Hoch- oder Tiefwert), sowie an einem Terrassenpunkt (Wendepunkt mit horizontaler Wendetangente) gilt jedoch:
f '(x) = 0
Die Monotonie ändert sich daher in jedem relativen Extrempunkt! In einem Terassenpunkt wird nur die strenge Monotonie unterbrochen (bei strenger Monotonie gelten nur das > oder < - Zeichen, bei Monotonie schlechthin ist auch das = - Zeichen zugelassen).
VOR einem Hochpunkt (rel. Maximum) ist f(x) monoton steigend, NACH einem Hochpunkt monoton fallend.
VOR einem Tiefpunkt (rel. Minimum) ist f(x) monoton fallend, NACH einem Tiefpunkt monoton steigend.
Mit diesem Wissen ist's nun nicht mehr so schwer. Wir ermitteln die Nullstelle der 1. Ableitung, dort ist (sind) das (die) Extremum (Extrema).
Der Bruch ist dann Null, wenn sein Zähler Null ist:
-(ln(x + 1) + 1) = 0
ln(x + 1) + 1 = 0
ln(x + 1) = -1
x + 1 = e^(-1)
x = (1/e) - 1 (= -0,63)
°°°°°°°°°°°°°
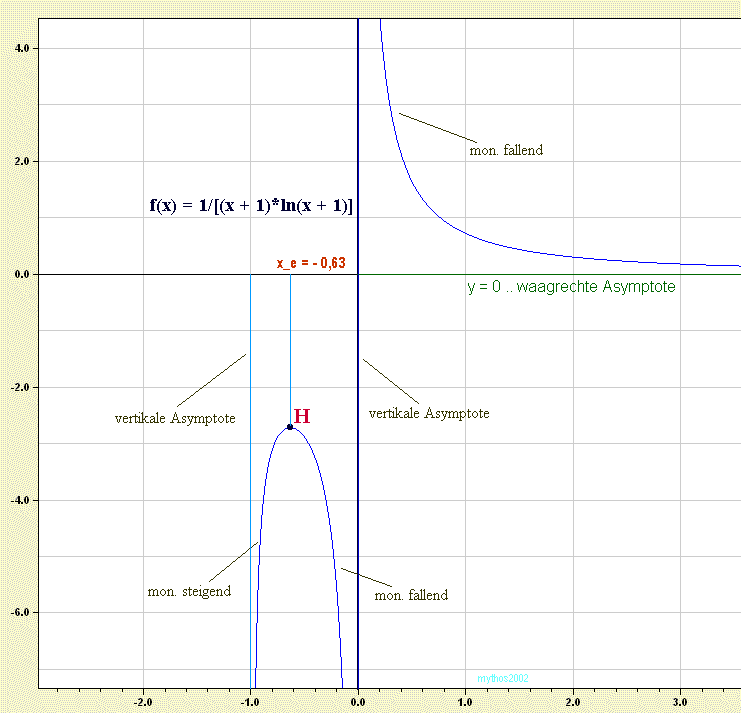
Bei der Besprechnung der Definitionsmenge haben wir die Stellen -1 und 0 ausgeschlossen, dort befinden sich - weil der Nenner jeweils Null wird - sogenannte Polstellen (mit vertikaler Asymptote), ausserdem müssen ja alle x > -1 sein.
Bestimme nun das Vorzeichen von f '(x) an einer Stelle links von -0,63 (z.B. bei -0,8), beachte dabei, dass der Nenner infolge des Quadrates immer positiv ist, du wirst ein positives Vorzeichen erhalten! Daher liegt bei x_e = -0,63 ein HOCHPunkt vor und die Monotonie kann wie folgt angegeben werden:
Monoton steigend in {x| -1 < x < -0,63}
Monoton fallend in {x| -0,63 < x < 0}
Monoton fallend in {x| 0 < x < +oo}
Eine Skizze (ich sende später noch den Graphen) macht dies dann noch deutlicher ...
Gr
mYthos
|
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 76
Registriert: 12-2002
| | Veröffentlicht am Dienstag, den 20. Januar, 2004 - 20:32: | 
|
zu 3)a)
Die Stellen,die in Df auch nicht enthalten,sind dürfen für Jk auch nicht in der neuen D*f liegen.
Dementsprechend würde ich sagen: Df=D*f
b)Wende die Regel INT(f´(x)/f(x)dx)= ln (f(x)) an.
(Geht aus einer der Substitutionsregeln hervor.)
Folglich: Jk= [ln(ln(x+1))]
c)-ln(ln(sqrt(e-1))+1)= ln(ln(x+1))
Nehmen wir an,dass der Term auf linken Seite für eine Zahl a steht:
a = ln(ln(x+1))
e^a= ln(x+1)
e^(e^a)=x+1
x= e^(e^a)-1
..und jetzt noch den Term einsetzen  ...kommt mir jetzt irgendwie ein bisschen komisch vor. ...kommt mir jetzt irgendwie ein bisschen komisch vor.
(Beitrag nachträglich am 20., Januar. 2004 von Kratas editiert) |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 888
Registriert: 03-2002
| | Veröffentlicht am Dienstag, den 20. Januar, 2004 - 22:01: | 
|
So, nun der Graph zu 1, wodurch die bisherigen Ergebnisse auch anschaulich werden.
Die waagrechte Asymptote erhalten wir durch Bestimmung des Grenzwertes der Funktion f(x) für x -> + oo (unendlich):
lim[x -> +oo][1/((x + 1)*ln(x + 1))] = 0, weil der Nenner gegen oo (unendlich) geht.
Schreibe bitte du nun einmal, wie weit du mitgekommen bist und wie's dann weitergehen soll.
Gr
mYthos
 |
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 68
Registriert: 09-2003
| | Veröffentlicht am Mittwoch, den 21. Januar, 2004 - 16:17: | 
|
VIELEN VIELEN DANK, dass ihr mir so viel weitergeholfen habt!!
@Mythos: danke auch für deine anschauliche Skizze!!!
Ich werd mich dann mal durch eure Antworten durcharbeiten...
 |
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 69
Registriert: 09-2003
| | Veröffentlicht am Sonntag, den 25. Januar, 2004 - 14:27: | 
|
Also ich habe soweit alles verstanden--> danke für die guten Erklärungen!!
@Mythos Ich hätte nur noch eine klitzkleine Nachfrage zum Intervall bei 1) und zwar: warum es offen ist?? weil die -1 ausgeschlossen ist? aber was ist mit oo??
@Kratas, bei 3.) habe ich leider nicht so viel verstanden. Was ist das für eine Substitutionsregel bei b)?? Ist das bei c) nicht richtig oder warum kommt dir das komisch vor???
Wie es weitergehen soll? Also bei der Tangente bei 1.) habe ich selbst keine Ansätze weil ich da nichts weiß, vielleicht könntest du mir trotzdem helfen?
genauso bei 2.)...
mfg Avril |
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 83
Registriert: 12-2002
| | Veröffentlicht am Sonntag, den 25. Januar, 2004 - 15:49: | 
|
Hallo Avril !
zu 3a) Es gibt eine Substitutionsregel,die lautet:
INT[ g(v(x)) * v´(x) dx ] = INT [ g(v(x)) ] dx
Das ist die umgekehrte Kettenregel von (g(v(x))´=
g(v(x))´*v´(x).Wenn du also einen Term hast, in dem du eine (innere)Funktion v findest, sowie deren Ableitung, kannst du das Integral bestimmen.
Beispiel:
f(x)= 2x * Wurzel aus (x^2+1)
v(x)= x^2+1
v´(x) = 2x
g(x)= Wurzel aus x
INT f(x) dx = INT g(v(x)) dx
= INT Wurzel aus x^2+1 dx = INT Wurzel aus v dv= [(2/3)*v^(3/2) ] = [(2/3)*(x^2+1)^(3/2) ]
*****************************************
Aus dieser Regel kann man nun diese neue ableiten:
INT (v´(x) / v(x)) dx = INT (1/f(x))*(f´(x))
Nach obiger Regel mit g(x)=1/x,v(x)=f(x),f´(x)=v´(x) gilt:
INT (v´(x) / v(x)) dx = INT 1/v dv = [ln v]
= [ ln f(x) ] q.e.d.
*********************
bei c)weiß ich auch nicht genau. Ich hab einfach nur die Gleichung nach x aufgelöst,nur,wie gesagt,ist der Term doch sehr ungewöhnlich...vielleicht ist Mythos in der Lage,das Problem zu lösen.
Gruß
Kratas |
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 84
Registriert: 12-2002
| | Veröffentlicht am Sonntag, den 25. Januar, 2004 - 16:00: | 
|
Zur Tangente:
Eine Tangente hat die Geradengleichung y=m*x+n
mit der Steigung m und den y-Achsendurchgang n
Da die Ableitung an einer Stelle a der Steigung der Tangente im Punkt P(a/f(a)) entspricht,musst du,um die Steigung zu erhalten, a in f´ einsetzen.
Um nun noch n zu bestimmen,setzt du in die Gleichung y=m*x+n die berechnete Steigung sowie die Koordinaten a und f(a) für x bzw. y ein. Nach n auflösen und du hast alle Informationen.Jetzt nur noch m und n in die allgemeine Form y=m*x+n einsetzen:Fertig!
MfG Kratas |
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 85
Registriert: 12-2002
| | Veröffentlicht am Sonntag, den 25. Januar, 2004 - 18:53: | 
|
Zu 2)
Wenn eine Funktion nicht streng monoton ist,dann nimmt die Funktion an mindestens zwei Stellen im Definitionsbereich den gleichen Wert an,z.B. die Funktion f(x)=x^2,sie fällt für -oo<x<0 und steigt für 0<x<+oo.Für x=2 und x=-2 ist f(x)=4
[oder f(2)=f(-2)=4 ] Wenn dies so ist dann ist die Funktion auf dem Definitionsbereich nicht eindeutig umkehrbar.Wenn man eine Umkehrfunktion einer Funktion haben will,muss man die Abbildungsrichtung der alten Funktion ändern.Normalerweise wird jedem x-Wert ein f(x)-Wert zugeordnet,d.h.f(x) ist von x abhängig,wir berechnen f(x) aus x.Bei der Umkehrfunktion ordnen wir nun jedem f(x)-Wert den entsprechenden x-Wert zu. also statt x->f(x) f(x)->x. Da die Definition einer Funktion aber sagt,dass dem 1.Wert nur ein 2.Wert zugeordnet werden darf,gibt es so von f(x)=x^2 keine Umkehrfunktion,
z.B. f(x)=4, welcher Wert soll diesem f(x)-Wert zugeordnet werden,wo doch sowohl x=2 als auch x=-2 in Frage kommen ?
Wenn nun eine Funktion streng monoton steigend ist, gibt es keine 2 x-Werte für der f(x)-Wert gleich ist, da gilt: f(x1)>bzw.<f(x2) für x1 ungleich x2.
zu b) zum Beispiel: f(x):
x für 0<_x<_1
3-x für 1<x<_2
Die Teilfunktionen sind auf den Definitionsbereichen umkehrbar eindeutig und außerdem sind deren Graphen Geraden,die parallel bzw. orthogonal auf der Gerade mit y=x stehen.
Umkehrfunktion kann man zeichnen,indem man den Graphen von f an der Gerade y=x spiegelt.In diesem Fall werden die einzelnen Punkte auf sich selber abgebildet bzw. gespiegelt.
Vielleicht kann das ja jemand anders das besser erklären ;)...
|
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 86
Registriert: 12-2002
| | Veröffentlicht am Sonntag, den 25. Januar, 2004 - 19:12: | 
|
zu 2b) Die x-Werte der Umkehrfunktion sind f(x)-Werte der Funktion.Also D(f)=W(g) und D(g)=W(f).
Wir suchen den x-Wert für den gilt:
1/((x+1)*ln(x+1))=1/e
Die Lösung dazu ist in 1c)versteckt:Dort ist der Punkt P(e-1 | 1/e) gegeben.Folglich: x=e-1
=>g(1/e)=e-1
Für die Ableitung der Umkehrfunktion gilt:
g´(y)=1/f´(x)
g´(1/e)= 1/....->f´(1/e) einsetzen!
Gruß
Kratas
|
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 87
Registriert: 12-2002
| | Veröffentlicht am Sonntag, den 25. Januar, 2004 - 19:38: | 
|
Hier noch ein paar Seiten aus einem Mathebuch:
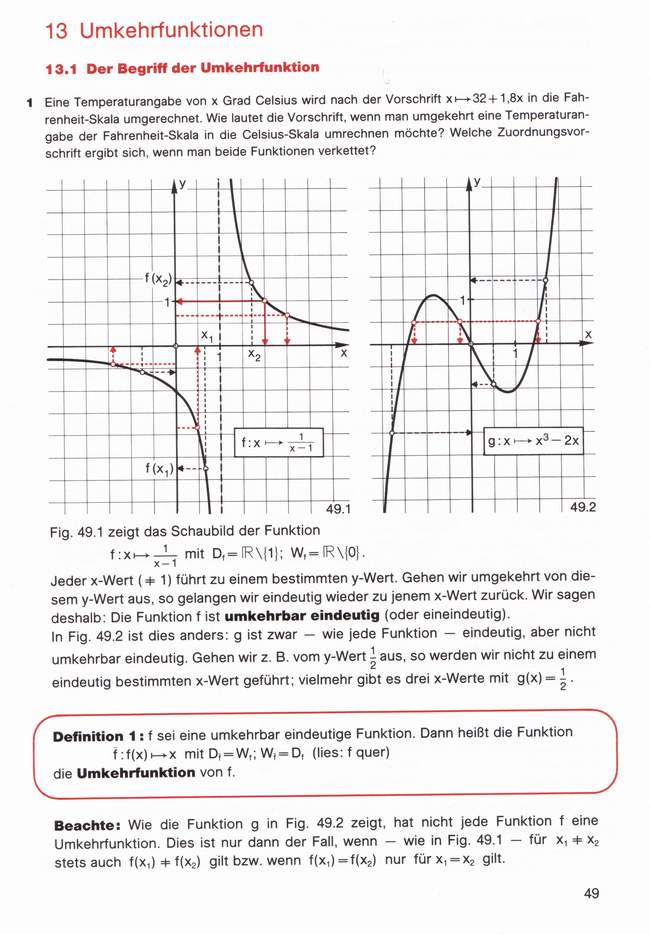
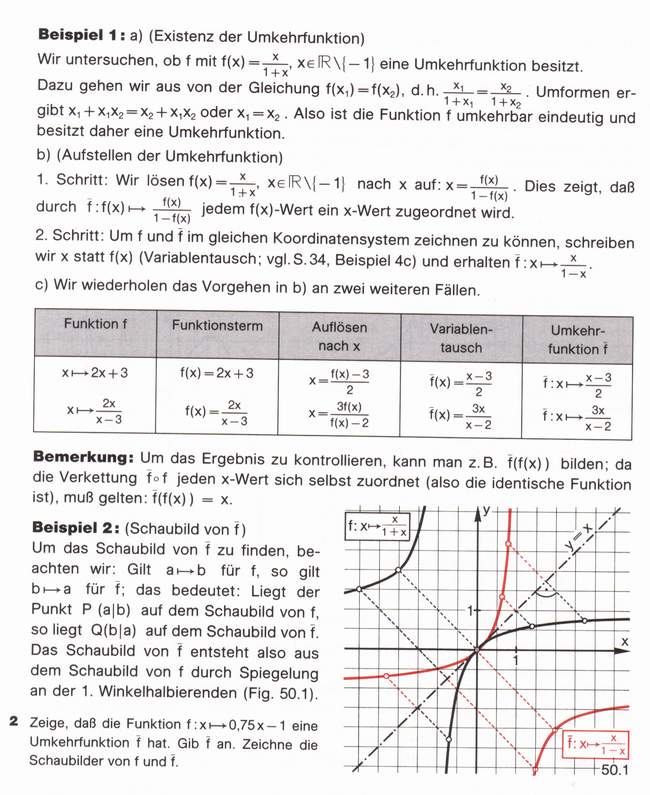
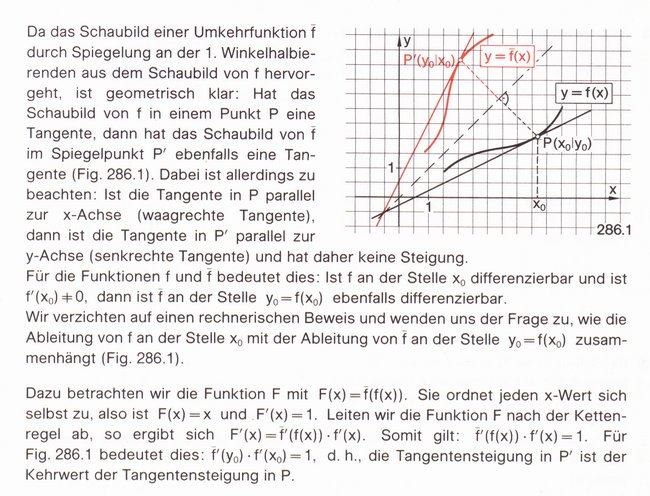

MfG  Kratas Kratas |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 891
Registriert: 03-2002
| | Veröffentlicht am Sonntag, den 25. Januar, 2004 - 19:45: | 
|
Hallo,
ja, -1 ist ausgeschlossen und rechts kann man ja nicht abschließen, weil oo nicht zu begrenzen ist; aber es kann sein, dass bei oo auch "]" zulässig ist (das ist sicher nicht so essentiell).
Nun zu der recht sperrigen Sache in 3.
Die gegenständliche Integralfunktion I(x) wird durch die Stammfunktion von f(t) mit variabler oberer Grenze x und zunächst fester unterer Grenze k gebildet. Durch nachfolgende Variation von k wird erst eine Schar I_k(x) dieser Integralfunktionen erzeugt.
I_k(x) = int[k;x][f(t)]dt
mit
int[f(t)dt = int[1/((t + 1)*ln(t + 1))]dt
Zur Ermittlung der integralfreien Darstellung muss zuerst das unbestimmte Integral von f(t) nach dt bestimmt und danach die Grenzen von k bis x eingesetzt werden:
Die Integration wird mit folgender Substitution gelöst:
ln(t+1) = u, dabei ist du/dt = 1/(t + 1) bzw. dt = du*(t + 1)
Somit kommt
int[1/((t + 1)*ln(t + 1))]dt = int(1/u)du = ln(u),
denn (t + 1) kürzt sich weg!
Rückeinsetzen aus der Substitution bringt
.. = ln(ln(t + 1)); nun die Grenzen einsetzen: ->
I_k(x) = ln(ln(t + 1))[k;x] = ln(ln(x + 1)) - ln(ln(k + 1))
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
k > 0;
Dk = {x | x > 0}, weil ln(x + 1) > 0, folgt x + 1 > 1 folgt x > 0
wird fortgesetzt
c.) kommt in einem neuen Beitrag
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 892
Registriert: 03-2002
| | Veröffentlicht am Sonntag, den 25. Januar, 2004 - 21:58: | 
|
3c.)
I_(e-1)(x) ist eine einzelne Funktion aus der Schar [für den Scharparameter k = e - 1]
I_(e-1)(x) = ln(ln(x + 1)) - ln(ln(e-1 + 1));
weil ln(ln(e-1 + 1)) = ln(ln(e)) = ln(1) = 0, ist
I_(e-1)(x) = ln(ln(x + 1))
°°°°°°°°°°°°°°°°°°°°°°°°°°
Nun soll die Gleichung
- I_(e-1)(sqrt(e - 1)) = ln(ln(x+1) nach x aufgelöst werden.
Für den Term auf der linken Seite ist in die Funktionsgleichung I_(e-1)(x) = ln(ln(x + 1) für das Argument x gleich der Wert sqrt(e - 1) einzusetzen:
- ln(ln(sqrt(e - 1) + 1)) = ln(ln(x + 1)
beide Seiten entlogarithmieren ->
1/ln(sqrt(e - 1) + 1) = ln(x + 1)
der linke Ausdruck wird berechnet und ist 1,193876, somit ist
1,193876 = ln(x + 1)
nochmals entlogarithmieren (als e^.. ausdrücken)
3,3 = x + 1
x = 2,3 E
°°°°°°°°°
Die Schar der Integralfunktionen Ik(x) stellt geometrisch die jeweilige Flächenfunktion des Graphen Gf der Kurve f(t) und der x-Achse innerhalb der Grenzen k und x dar und dies in Abhängigkeit von der oberen Grenze x.
Bei der Funktion I_(e-1)(x) ist dies die Fläche, die Gf in den Grenzen von e - 1 und x mit der x-Achse einschließt.
Beim Auflösen der letzten Gleichung wird jene Stelle x gesucht, für diese Fläche gleich einem vorgegebenen Wert ist. Hier befindet sich diese Fläche also in den Grenzen von 1,72 bis 2,3 (Einheiten), ihre Größe beträgt 0,1772 E².
Gr
mYthos
(Beitrag nachträglich am 25., Januar. 2004 von mythos2002 editiert) |
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 72
Registriert: 09-2003
| | Veröffentlicht am Dienstag, den 27. Januar, 2004 - 14:57: | 
|
Hi Kratas & Mythos!!
DANKESCHÖN dass ihr mir nochmal weitergeholfen habt!!! Ich habe mich echt gefreut! 
Danke Kratas auch für die Seiten aus dem Mathebuch!
Also 1) habe ich mit der Tangente nun komplett verstanden.
2a) auch , wobei ich bei b) etwas anders vorgegangen bin, aber es hat alles geklappt!
Die Regel bei 3) habe ich mir verinnerlicht;
Habe hier aber noch zwei Fragen:
bei a) verstehe ich nicht ganz warum D = R+ ist.
"k > 0;
Dk = {x | x > 0}, weil ln(x + 1) > 0, folgt x + 1 > 1 folgt x > 0 "
bei der Erklärung von Mythos weiß ich nämlic nicht,
warum ln(x + 1) > 0????
Bei c) habe ich mich leider vertippt, denn die Wurzel bezieht sich nur auf e!!
Jetzt ist meine Frage wie sich das auf das Endergebnis auswirkt???
und wo hast du die Größe von 1,772 E^2 her?
Sonst war aber alles prima erklärt!!!
Mfg, Avril
|
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 89
Registriert: 12-2002
| | Veröffentlicht am Dienstag, den 27. Januar, 2004 - 16:23: | 
|
Es ergibt sich dann für 3c):
-ln(ln(sqrt(e)-1+1)=ln(ln(x+1))
-ln(ln e^(1/2))=ln(ln(x+1))
-ln(1/2)=ln(ln(x+1))
ln 2 =ln(ln(x+1))
e^(e^ln 2)= x+1
x = e^2 - 1
************
Gruß 
Kratas |
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 73
Registriert: 09-2003
| | Veröffentlicht am Mittwoch, den 28. Januar, 2004 - 08:04: | 
|
Hi Kratas!
Die Umformungen auf beiden Seiten kann ich leider nicht ganz nachvollziehen! Könntest du noch mal sagen was du da genau gemacht hast? Geht das auch einfacher?
danke, Avril |
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 98
Registriert: 12-2002
| | Veröffentlicht am Mittwoch, den 28. Januar, 2004 - 16:01: | 
|
Zunächst einmal habe ich den Term -ln(ln(sqrt(e)-1+1) vereinfacht.
*-1+1(=0)fällt weg
*Es gilt allgemein: n-te Wurzel aus a = a^(1/n)
=>sqrt(e)=e^(1/2)
*ln und e^... sind Gegenoperationen und heben sich deshalb gegenseitig auf.
(Dementsprechend gilt also allgemein
e^(ln x)=x
ln (e^x) = x
Diese Umformung ist sehr nützlich,wenn man Logarithmus-oder Exponentialgleichungen lösen will(siehe unten)
*Desweiteren gibt es auch folgende Logarithmusgesetze:
Die Basis ist a
log b + log c = log (b*c)
log b - log c = log (b/c)
log b^c = c*log b
Ich habe die letzte Regel angewandt.
|
    
Kratas (Kratas)

Erfahrenes Mitglied
Benutzername: Kratas
Nummer des Beitrags: 99
Registriert: 12-2002
| | Veröffentlicht am Mittwoch, den 28. Januar, 2004 - 16:54: | 
|
Also: ln 1/2 = ln (2^-1) = - ln 2
So nun steht da nur noch eine Gleichung:
ln 2 = ln(ln(x+1))
Bei Lösen von Gleichungen ist man bestrebt die Gleichung auf die Form x=...zu bringen.
Beispiele: log(2)x = 8
<=> 2^(log(2)x) = 2^8
<=> x = 2^8 = 32
ln x ist der natürliche Logarithmus,der Logarithmus von x zur Basis e(=Eulersche Zahl)
log(e)x=ln x
Dementsprechend nach obigem Beispiel:
ln x = 2
e^(ln x)= e^2
e^(log(e)x)=e^2
x = e^2
Ein anderes Beispiel:
4^x = 16
<=>log(4)4^x = log(4)16
<=>x = log(4)16 = 2
Nun ist e die Basis der Potenz:
e^x = 4
ln(e^x) = ln 4
log(e)(e^x)=ln 4
x = ln 4
Fazit: Um Logarithmen verschwinden zu lassen, auf beiden Seiten die Potenz bilden mit der Basis des Logarithmus,bei Potenzen den Logarihmus bilden mit der Basis der Potenz.
Damit können wir dann unsere Gleichung ganz einfach lösen:
ln(ln(x+1))= ln 2
log(e)(ln(x+1)) = ln 2
e^(log(e)(ln(x+1))= e^(ln 2)
ln(x+1) = 2
e^(ln(x+1))=e^2
x+1=e^2
x=e^2-1
********
|
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 74
Registriert: 09-2003
| | Veröffentlicht am Donnerstag, den 29. Januar, 2004 - 19:47: | 
|
Danke, Kratas!! Dank der Erklärungen habe ich´s verstanden Dank der Erklärungen habe ich´s verstanden
@Mythos: könntest du noch mal auf meine Fragen an dich antworten?? Wäre sehr nett, denn dann ist alles geklärt! |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 908
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 29. Januar, 2004 - 23:48: | 
|
Ahhh, ich verganz gas!
Nun, zunächst zur Frage, warum x > 0 ist:
Es gilt ja für die Schar der Integralfunktionen
I_k(x) = ln(ln(t + 1))[k;x] = ln(ln(x + 1)) - ln(ln(k + 1)) und k > 0;
Weil die ln-Funktion zwei Mal hintereinander kommt (also der Logarithmus vom Logarithmus), muss zunächst der innerste Logarithmus > 0 sein, denn sonst könnte man den äußeren Logarithmus nicht bilden!
Also
ln(x + 1) > 0 .. diese Ungleichung nun entlogarithmieren (als e-Potenz)
[Hinweis:
Weil die ln-Funktion monoton (steigend) ist, kann man die Ungleichung wie eine Gleichung behandeln (das Ungleichheitszeichen ändert sich nicht)]
x + 1 > 1 (weil e^0 = 1), 1 subtrahieren, somit
x > 0
°°°°°
Dann:
Von wo ich die Größe 1,772 E² habe? Ganz einfach, ausgerechnet! Die Grenzen sind bekannt, das Integral auch, also nur noch einsetzen.
Natürlich wirkt sich der Tippfehler (den habe ich fast von Anfang an vermutet!) auf das Ergebnis aus, aber prinzipiell ist die Rechnung die gleiche (die müsstest du eigentlich nun können ...).
....
I_(e-1)(x) = ln(ln(x + 1))
°°°°°°°°°°°°°°°°°°°°°°°°°°
Nun soll die Gleichung
- I_(e-1)(sqrt(e) - 1) = ln(ln(x+1) nach x aufgelöst werden.
Für den Term auf der linken Seite ist in die Funktionsgleichung I_(e-1)(x) = ln(ln(x + 1) für das Argument x gleich der Wert sqrt(e) - 1 einzusetzen:
- ln(ln(sqrt(e) - 1 + 1) = ln(ln(x + 1)
beide Seiten entlogarithmieren ->
1/ln(sqrt(e)) = ln(x + 1)
der linke Ausdruck wird wieder berechnet und ist 1/(1/2) = 2, somit ist
2 = ln(x + 1)
nochmals entlogarithmieren
e² = x + 1
x = (e² - 1) E
°°°°°°°°°°°°°°
Die Schar der Integralfunktionen I_k(x) stellt geometrisch die jeweilige Flächenfunktion des Graphen Gf der Kurve f(t) und der x-Achse innerhalb der Grenzen k und x dar und dies in Abhängigkeit von der oberen Grenze x.
Bei der Funktion I_(e-1)(x) ist dies die Fläche, die Gf in den Grenzen von e - 1 und x mit der x-Achse einschließt.
Beim Auflösen der letzten Gleichung wird jene Stelle x gesucht, für diese Fläche gleich einem vorgegebenen Wert ist. Hier befindet sich diese Fläche also in den Grenzen von (e - 1) d.i. 1,72 bis (e² - 1) (Einheiten), ihre Größe beträgt 0,6931 E², das ist genau ln(2) E².
Daher muss man diese Fläche A auch allgemein aus der Integralfunktion I_(e-1)(x) berechnen können:
A = I_(e-1)(x) = ln(ln(x + 1))in den Grenzen [(e-1);(e²-1)]
A = ln(ln(e²)) - ln(ln(e)
A = ln(2) - ln(1),da ln(1) = 0 ist
A = ln(2)
°°°°°°°°°
Na, ist das nicht schön?
Gr
mYthos
|
    
Avril_01 (Avril_01)

Erfahrenes Mitglied
Benutzername: Avril_01
Nummer des Beitrags: 77
Registriert: 09-2003
| | Veröffentlicht am Samstag, den 31. Januar, 2004 - 16:17: | 
|
JA, das ist schön!!!
Ein ganz großes Dankeschön!!  
Wollte zwar nur, dass du mir noch mal erklärt warum R+ und wie du auf die Fläche bei c) kamst...
bei c) wo ich mich vertippt hatte mit Wurzel von e, hat mir nämlich schon Kratas weitergeholfen (s.oben), aber das ist ja egal.. doppelt hält besser!!! Und nun ist alles verstanden!*freu*
Noch mal danke an euch beide! |
|