| Autor |
Beitrag |
    
Detlef01 (Detlef01)

Erfahrenes Mitglied
Benutzername: Detlef01
Nummer des Beitrags: 345
Registriert: 01-2003
| | Veröffentlicht am Dienstag, den 09. Dezember, 2003 - 15:05: | 
|
hi,
ich verstehe die schreibweise bei ober- und untersumme nicht?
f(x) = x² intervall von 0 bis b; in n gleiche teile!
U = b/n(b/n)²+b/n(2b/n)²+...+b/n((n-1)b/n)²
wie kommt man darauf und wie unterscheidet sich die obersumme davon?
detlef |
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 356
Registriert: 10-2003
| | Veröffentlicht am Dienstag, den 09. Dezember, 2003 - 15:39: | 
|
Du zerlegst doch die Fläche von 0 bis b unter dem Graphen in n Streifen. Bei der Untersumme legst du in jedem Streifen ein Rechteck fest, dass so hoch ist, dass es sich gerade noch unterhalb des Graphen befindet. Seine Breite ist b/n. Seine Höhe ist so hoch wie der niedrigste Punkt des Graphen innerhalb des Streifens. Das ist bei dieser Funktion der Punkt an der linken Grenze. Das erste Rechteck hat die Höhe 0 (und taucht in deiner Summe oben nicht auf). Das zweite hat die Höhe (b/n)² (Funktionswert bei x=b/n) usw. Das letzte hat die Höhe ((n-1)b/n)² (Funktionswert am Beginn des letzten Intervalls).
Bei der Obersumme geht man ähnlich vor, nimmt aber solche Rechtecke, die gerade eben aus dem Streifen herausragen. Ihre Höhe ist so groß wie der höchste Punkt des Graphen in diesem Streifen. Bei dieser Funktion liegt der Punkt an der rechten Grenze des Streifens. Es ergeben sich:
als Breite weiterhin b/n, als Höhen dieselben wie oben, jedoch mit dem letzten Element (n*b/n)²(Funktionswert am Ende des letzten Intervalls).
Mit freundlichen Grüßen
Jair
|
    
Detlef01 (Detlef01)

Erfahrenes Mitglied
Benutzername: Detlef01
Nummer des Beitrags: 346
Registriert: 01-2003
| | Veröffentlicht am Dienstag, den 09. Dezember, 2003 - 17:17: | 
|
ok, vielen danke!
habe jetzt mal was gerechnet:
f(x) = 1/2x intervall 2 bis 4
b = 4-2 = 2
n = 4
breite = 1/2
Summe Ui = 1/2*f(2)+1/2*f(2,5)+1/2*f(3)+1/2*f(3,5)
= 2,75
Summe Oi = 1/2*f(2,5)+1/2*f(3)+1/2*f(3,5)+1/2*f(4)
= 3,25
(Ui+Oi)/2 = A = 3cm²
??
ist das auch so auf kompliziertere fkt. übertragbar?
detlef |
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 362
Registriert: 10-2003
| | Veröffentlicht am Dienstag, den 09. Dezember, 2003 - 19:03: | 
|
So in etwa. Du musst allerdings den Grenzwert der Ober- und der Untersummen bilden (für n ®¥). Wenn die beiden Grenzwerte gleich sind (das ist bei "gewöhnlichen" Funktionen der Fall), dann nennt man den gemeinsamen Grenzwert das Integral der Funktion in dem betrachteten Intervall. Und dieses Integral ist unter bestimmten Voraussetzungen der Flächeninhalt.
Hm, in deinem anderen Thread benutzt du das Ganze doch schon. Wie läuft denn der Unterricht bei euch? Macht ihr gleichzeitig sozusagen Theorie und Praxis?
Mit freundlichen Grüßen
Jair
|
    
Detlef01 (Detlef01)

Erfahrenes Mitglied
Benutzername: Detlef01
Nummer des Beitrags: 349
Registriert: 01-2003
| | Veröffentlicht am Mittwoch, den 10. Dezember, 2003 - 12:54: | 
|
ja, ich habe probleme, mir das ganze vorzustellen und die herleitungen und beweise für die flächenberechnung durch integrieren vorzustellen! wieso kann man durch integrieren den flächeninhalt berechnen, wie kann man das beweisen??
detlef |
    
Jule_h (Jule_h)

Erfahrenes Mitglied
Benutzername: Jule_h
Nummer des Beitrags: 109
Registriert: 03-2003
| | Veröffentlicht am Mittwoch, den 10. Dezember, 2003 - 13:34: | 
|
wie Jair schon sagte: unter gewissen Voraussetzungen kann man ja so eine Fläche gut annähern indem man eine Treppe "drunterbaut" und eine "darüber". Wenn man dann die "Treppenstufen" immer schmaler macht, erhält man eine immer bessere Näherung des Fächeninhalts. Etwas unwissenschaftlich ausgedrückt läuft die Sache so ähnlich wie ihr vermutlich in der 10.Klasse den Kreisinhalt bzw. Umfang durch Vielecke angenähert habt: durch ständige Vermehrung der Eckenzahl. Hier vermehrst du beständig die Zahl der Treppenstufen indem du sie immer schmaler machst...Allerdings wundere ich mich auch wie das im Unterricht läuft wenn ihr gleichzeitig schon Integrale berechnet?? |
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 369
Registriert: 10-2003
| | Veröffentlicht am Mittwoch, den 10. Dezember, 2003 - 13:35: | 
|
Hallo Detlef,
ich will mal versuchen, einen Überblick zu geben. Nach deinen Ausführungen oben gehe ich jetzt davon aus, dass du einerseits zwar Integrale bilden kannst, um sozusagen nach Kochrezept damit Flächeninhalte zu berechnen, dass du andererseits bereits Ober- und Untersummen kennen gelernt hast, dass dir aber der Zusammenhang zwischen diesen beiden Teilen noch nicht bekannt ist.
Dass man aber mit Hilfe von Unter- und Obersummen Flächeninhalte berechnen kann, hast du ja schon in Übungen erarbeitet. Die Berechnung wird genauer, wenn man die Breite der Intervalle kleiner macht. Ideal ist es, wenn es einen Grenzwert der Unter- und Obersummen gibt, wenn die Intervallbreite gegen 0 geht, und wenn diese beiden Grenzwerte auch noch gleich sind. Da dabei gleichzeitig die Anzahl der Intervalle gegen ¥ geht, müssen diese Grenzwerte keineswegs 0 sein. Es gibt übrigens durchaus auch Funktionen, bei denen die Grenzwerte der Ober- und Untersummen nicht übereinstimmen. Diese Funktionen sind allerdings schon ziemlich exotisch. (Wenn du willst, kann ich dir aber mal eine nennen.)
Dieser gemeinsame Grenzwert wird Integral genannt. Es handelt sich tatsächlich um dasselbe Integral, das du auch über die Stammfunktionen berechnet hast. Dass man auf beide Weisen, also über die Ober- und Untersummen und über die Stammfunktionen, zum Integral kommen kann, zeigt der sogenannte Hauptsatz der Infinitesimalrechnung. Wenn du willst, kann ich dir den Beweis erklären. (Allerdings brauche ich dazu etwas mehr Ruhe, als ich hier habe... ). ).
Der Hauptsatz sagt aus, dass man unter bestimmten, relativ häufig vorhandenen Voraussetzungen zum Integral kommen kann (also zum Grenzwert der Unter- und der Obersummen), indem man eine Stammfunktion zur gegebenen Funktion herstellt, die untere und obere Grenze einsetzt und die Differenz berechnet.
Zumindest wenn die betrachtete Funktion im Intervall nur oberhalb der x-Achse verläuft, stellt das Integral dann die Fläche zwischen Graph und x-Achse dar. Verläuft sie nur unterhalb, so erhält man den Flächeninhalt mit negativem Vorzeichen. Schneidet sie die x-Achse, so ergibt sich die Differenz der beiden Teilflächen unter- und oberhalb. Will man in diesem Fall trotzdem die Gesamtfläche haben, muss man das Integral eben in zwei Teilintegrale zerlegen (mit der Schnittstelle einmal als oberer und einmal als unterer Grenze) und muss die Beträge der Teilintergrale ermitteln.
Mit freundlichen Grüßen
Jair
|
    
Detlef01 (Detlef01)

Erfahrenes Mitglied
Benutzername: Detlef01
Nummer des Beitrags: 351
Registriert: 01-2003
| | Veröffentlicht am Mittwoch, den 10. Dezember, 2003 - 15:47: | 
|
es wäre echt super, wenn du mir den hauptsatz erklären könntest, weil ich besser damit umgehen kann, wenn ich die beweise kenne!
danke für die super einführung!
detlef |
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 370
Registriert: 10-2003
| | Veröffentlicht am Mittwoch, den 10. Dezember, 2003 - 21:10: | 
|
Hi Detlef,
gehen wir's also an:
Zunächst einmal brauchen wir eine etwas ungewöhnlich aussehende Funktion mit Namen F0. Diese Funktion ist definiert als
F0(x)=ò0 xf(t)dt.
Man nennt sie Integralfunktion.
Der eigentliche Beweis verläuft in 3 Schritten. Im 1. Schritt zeigen wir, dass die Integralfunktion eine Stammfunktion ihrer Integrandfunktion (der Funktion f) ist.
f(x) soll dabei über [0;x] stetig sein, der Grenzwert der Unter- und Obersummen soll existieren und übereinstimmen und f(x) soll auerdem eine Stammfunktion besitzen. (Man kann zeigen, dass alle stetigen Funktionen diese Voraussetzungen erfüllen.) Zur besseren Vorstellung soll x>0 und f(x) in [0;x] ebenfalls positiv sein. Dies sind jedoch keine notwendigen Voraussetzungen.
Betrachte mal die Skizze unten:

Sie zeigt den Flächeninhalt "unter" dem Graphen einer Funktion f im Intervall [x;x+h]. Diesen Flächeninhalt beschreibe ich nun mit Hilfe der Funktion F0. Er beträgt
F0(x+h) - F0(x).
Dazu habe ich zunächst den Flächeninhalt zwischen den Grenzen 0 und x+h beschrieben, dann den zwischen 0 und x und die beiden Werte voneinander subtrahiert. Das ergibt den Inhalt der Fläche zwischen x und x+h.
Zur nächsten Skizze:
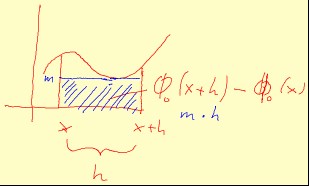
m ist das Minimum der Funktionswerte im Intervall [x;x+h]. (Man kann zeigen, dass es existiert). Das blaue Rechteck hat dann den Flächeninhalt m*h.
Und hier:
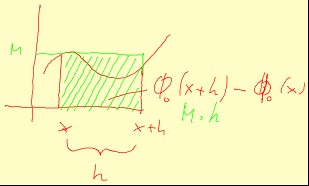
hier ist M das Maximum der Funktionswerte. Das grüne Rechteck hat den Flächeninhalt M*h.
Allgemein lässt sich sagen:
m*h £ F0(x+h)-F0(x) £ M*h
Dividieren wir die gesamte Ungleichung durch h>0 (für h<0 drehen sich zwar die Vergleichszeichen um, die Rechnung verläuft aber analog.)
m £ (F0(x+h)-F0(x))/h £ M
Bilden wir nun in allen 3 Ausdrücken den Grenzwert für h ® 0.
Dann geht das Minimum der Funktionswerte gegen f(x), das Maximum der Funktionswerte ebenso.
Dazwischen eingeschlossen ist
limh->0(F0(x+h)-F0(x))/h
Daraus folgt: der Grenzwert existiert. Und wie wir aus der Differentialrechnung wissen, bedeutet das, dass man die Funktion ableiten kann. Der Grenzwert ist dann F'(x).
Wir haben also gezeigt, dass die Integralfunktion eine Stammfunktion zu f (ihrer sog. Integrandfunktion) ist.
Schritt 1 ist geschafft.
(wird fortgesetzt)
Mit freundlichen Grüßen
Jair
|
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 371
Registriert: 10-2003
| | Veröffentlicht am Mittwoch, den 10. Dezember, 2003 - 21:16: | 
|
Teil 2 ist ein wichtiger Hilfssatz:
Zwei Stammfunktionen F und G zu einer Funktion f unterscheiden sich nur um eine Konstante.
Beweis:
F und G sollen Stammfunktionen zu f sein. Das bedeutet: F' = f und G' = f.
Betrachen wir die Funktion H = F - G.
Es gilt H' = (F-G)' = F' - G' = f - f = 0.
Da die Ableitung von H also 0 ist, muss H eine konstante Funktion sein: H(x) = c.
Also: c = H(x) = F(x) - G(x)
G(x) + c = F(x)
Die beiden Funktionen unterscheiden sich also nur um eine Konstante. Da wir keine besonderen Bedingungen für F und G gefordert haben, gilt das für alle Paare von Stammfunktionen zu f.
(Fortsetzung folgt.)
Mit freundlichen Grüßen
Jair
|
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 372
Registriert: 10-2003
| | Veröffentlicht am Mittwoch, den 10. Dezember, 2003 - 21:23: | 
|
Teil 3:
Kommen wir zurück zu der Fläche "unter dem Graphen von f " im Intervall [x; x+h]
Wir wissen schon, dass diese Fläche durch (F0(x+h)-F0(x)) ausgedrückt werden kann, und dass F0 eine Stammfunktion zu f ist.
Betrachten wir doch mal eine beliebige andere Stammfunktion zu f. Nennen wir sie F. Wir wissen aus Teil 2, dass sich F und F0 nur um eine Konstante (c) unterscheiden. Es gilt also
F0(x)=F(x)+c und
F0(x+h)=F(x+h)+c
Setzen wir mal ein:
Die Fläche ist
F0(x+h)-F0(x)=
(F(x+h)+c) - (F(x)+c)=
F(x+h) - F(x)
Wir benötigen also gar nicht unbedingt F0. Jede andere Stammfunktion zu f tut's genauso gut.
Wenn du jetzt noch x+h durch b ersetzt und x durch a, dann erhältst du schließlich die Endform des Satzes
òa bf(x)dx = F(b) - F(a)
So, ich hoffe, es war einigermaßen verständlich.
Mit freundlichen Grüßen
Jair
|
    
Detlef01 (Detlef01)

Erfahrenes Mitglied
Benutzername: Detlef01
Nummer des Beitrags: 358
Registriert: 01-2003
| | Veröffentlicht am Donnerstag, den 11. Dezember, 2003 - 10:19: | 
|
wow, super, vielen dank!
ich glaube ich habe es einigermaßen verstanden..werde es nochmal in ruhe durchgehen!
detlef |
|