| Autor |
Beitrag |
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 81
Registriert: 07-2003
| | Veröffentlicht am Donnerstag, den 13. November, 2003 - 17:39: | 
|
Schar der Funktion
fa(x) = (2*e^x)/(a + e^2x) mit a aus R+ und D=R
1)
a)Zeigen Sie die Gültigkeit folgender Beziehung
fa(ln Wurzel aus a + d) = fa(ln Wurzel aus a - d)
mit d Element aus R
(nur zur Info, nur das a steht unter der wurzel, das d nicht!)
muss ich das jetzt einsetzen??
Welche geometrische Bedeutung hat diese Beziehung für die Graphen Ga? |
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 82
Registriert: 07-2003
| | Veröffentlicht am Donnerstag, den 13. November, 2003 - 17:42: | 
|
b)
Untersuchen Sie das Verhalten von fa für x gegen +/- Unendlich.
Geben Sie die Monotoniebereiche sowie die Lage und Art des Extrempunktes an.
Bestimmen Sie die Ortskurve der extrempunkte aller graphen Ga.
Was ist eine Ortskurve? kann mir auch bei der teilaufgabe jmd. weiterhelfen??
|
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 83
Registriert: 07-2003
| | Veröffentlicht am Donnerstag, den 13. November, 2003 - 17:46: | 
|
2)
Gegeben ist die Integralfkt.
F: x= Integral von 0 bis x f1(t) dt
mit DF= R
also so weit ich das verstanden habe, muss man für a=1 einsetzen und F(x)-F(0) rechnen
Die integralfreie Darstellung von F(x) ist
2*arc tan e^x - pi/2, mithilfe der Substitutionsmethode
aber wie komme ich darauf??? |
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 84
Registriert: 07-2003
| | Veröffentlicht am Donnerstag, den 13. November, 2003 - 17:51: | 
|
folgende Aufgaben soll man noch ohne Berechnung des Integrals bearbeiten
a) Weisen Sie nach, dass F streng monoton steigt und dass der Graph F zum Ursprung symmetrisch ist.
b) zeigen Sie, dass GF genau einen Wendepunkt W hat und geben Sie seine Koordianten an.
Ermitteln Sie eine Gleichung der Wendetangente.
c) Für b > 0 gilt: F(b) > b* f1(b)
Begründen Sie diese Aussage anschaulich mit Hulfe einer Flächenbetrachtung.
Zeigen Sie, dass sich die Graphen GF und G1 im Bereich 0<x<1 genau einmal schneiden.
|
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 85
Registriert: 07-2003
| | Veröffentlicht am Donnerstag, den 13. November, 2003 - 17:54: | 
|
jetzt darf man mit der stammfunktion arbeiten...
e) Berechnen Sie dne Inhalt der sich beidseitig ins Unendliche erstreckenden Fläche zwischen G1 und der x-Achse.
f) Bestimmen Sie x0 so, dass F(x0) = 1 ist.
Das ist alles sehr viel, aber ich habe das extra aufgeteilt, in der Hoffnung, dass es so leichter fällt, mir bei einer Aufgabe zu helfen!
ich bin für jede Hilfe (bei einer Teilaufgabe) dankbar!!!
mfg, Carrie |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 745
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 13. November, 2003 - 19:31: | 
|
1)
Wir berechnen zunächst e^x für die beiden Stellen ln(sqrt(a)) + d und ln(sqrt(a)) - d, danach e^(2x) als das Quadrat von e^x [also e^(2x) = (e^x)²]:
e^(ln(sqrt(a) + d) = e^(1/2)*e^d = d*sqrt(a)
und
e^(ln(sqrt(a) - d) = e^(1/2)/e^d = (1/d)*sqrt(a)
weil e^(ln(a)) = a und e^((1/2)*ln(a)) = sqrt(a)
die entsprechenden Quadrate sind:
a*d² bzw. a/d²; die Werte für die e-Potenzen nun in fa einsetzen:
fa(ln(sqrt(a) + d) = 2*d*sqrt(a)/(a + a*d²) = 2*d*sqrt(a)/[a*(d² + 1)]
und
fa(ln(sqrt(a) - d) = [2*sqrt(a)/d]/(a + a/d²) =
= 2*d²*sqrt(a)/[d*a*(d² + 1)] = 2*d*sqrt(a)/[a*(d² + 1)]
Wir sehen nun, dass die beiden Funktionswerte gleich sind. Geometrisch bedeutet dies, dass die Funktion bezüglich der Stelle x = a symmetrisch ist (Symmetrieachse ist die Gerade X = (a;0) + t*(0;1) bzw. x = a).
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 746
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 13. November, 2003 - 20:17: | 
|
!! Ein kleiner Fehler hat sich bezüglich der Symmetrie eingeschlichen, die Symmetrie besteht natürlich bezüglich x = ln(sqrt(a) [und nicht x = a] !!
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 747
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 13. November, 2003 - 21:09: | 
|
(1)
Da a € R+ (a > 0) ist der Nenner stets > 0, und es existiert keine Polstelle (senkrechte Asymptoten).
Für den Grenzwert für x -> + oo muss man den Bruch umformen, indem man Zähler und Nenner durch e^(2x) dividiert:
lim(fa)(x -> oo) = lim [(2/e^x) / (a/(e^(2x)) + 1)
Die Brüche mit e^x und e^(2x) im Nenner gehen gegen Null, somit ist
lim(fa)(x -> oo) = 0/1 = 0
Die positive x-Achse ist somit Asymptote der Funktion.
Wegen der vorhin bewiesenen Symmetrie muss das auch für die negative x-Achse gelten! Aber man kann dies auch rechnerisch zeigen:
Für x -> -oo setzen wir x = -x1, mit x1 >= 0, damit geht x1 -> +oo
Dann ist fa(x) = fa(-x1) = 2*(e^(-x1))/(a + e^(-2x1)) = 2/[(e^x1)*(a + 1/(e^(2x1)))]
für x1 -> +oo geht der Nenner über alle Grenzen und der Grenzwert der ganzen Funktion fa ist auch für die "negative Seite" = 0
lim(x1 -> oo)[ 2/[(e^x1)*(a + 1/(e^(2x1)))] ] =
lim(x1 -> oo)[ 2/[(e^x1)*(a + 0)] ] = 0
Die x-Achse ist daher sowohl in positiver als auch in negativer Richtung Asymptote.
Wir vermuten klarerweise das Extremum an der Symmetriestelle, also bei ln(sqrt(a)) = (1/2)*ln(a) und berechnen dieses auch:
Beim Extremum gilt: fa'(x) = 0
fa'(x) = (Bruchregel) .. = 2*(e^x)*(a - e^(2x))/(a + e^(2x))²
Der Zähler wird Null gesetzt, der einzige Faktor, der Null werden kann, ist a - e^(2x)
e^(2x) = a
2x = ln(a)
x = x_extr = (1/2)*ln(a) = ln(sqrt(a))
y = fa_extr = fa(x_extr) = 2*sqrt(a)/(a + a) = 1/sqrt(a)
Die Ortskurve, auf der alle diese Extrema liegen, ergibt sich durch Variation des Parameters a. Wenn man diesen Parameter aus den beiden Gleichungen für x und y eliminiert, ergibt sich die Gleichung der Ortskurve in x, y:
x = (1/2)*ln(a)
y = 1/sqrt(a)
----------------
a = e^(2x) ->
sqrt(a) = e^x ->
y = 1/e^x = e^(-x)
Die Ortskurve für alle durch Variation von a entstehenden Extremwerte lautet:
y = e^(-x)
°°°°°°°°°°
Das Vorzeichen der 2. Ableitung an der Stelle x_extr gibt die Art des Extremums an, nach einiger Rechnung (ev. Regel (u/v)' = 0 -> (u/v)'' = u'/v verwenden) kommt
fa''(x_extr) = [2/(a + e^(2x))²]*(a - 3*e^(2x))
fa''(x_extr) = [2/(a + e^(2x))²]*(e^x)*(a - 3*e^(2x))
sgn(fa''(ln(sqrt(a))) = sgn (a - 3a) = -1
sgn = Vorzeichenfunktion
Da die 2. Ableitung an der Extremstelle < 0 ist, liegt ein (einziger) Hochpunkt vor.
Dadurch kann auch die Frage nach der Monotonie leicht beantwortet werden:
Im Intervall [-oo; ln(sqrt(a))], also "vor" dem Maximum ist fa monoton steigend, danach, im Intervall [ln(sqrt(a)); +oo] monoton fallend.
Eventuell füge ich noch eine Grafik an ....
Bemerkung: Es gibt noch zwei symmetrisch liegende Wendepunkte, in denen sich jeweils das Krümmumgsverhalten ändert.
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 748
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 13. November, 2003 - 21:37: | 
|
(1)
Hier noch die Grafik:
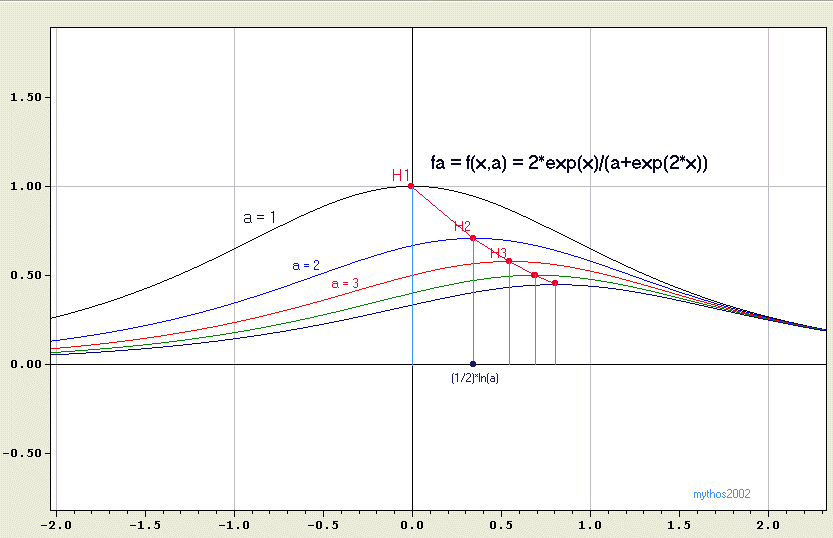 |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 750
Registriert: 03-2002
| | Veröffentlicht am Freitag, den 14. November, 2003 - 17:14: | 
|
Hi!
Du wirst Verständnis dafür haben, dass ich, wenn überhaupt, erst dann weitere deiner Fragen beantworte, bis ich von dir ein Feedback erhalten habe.
Leider ist es immer wieder zu beobachten, dass nach einer Bearbeitung des Beitrages nur noch das Schweigen im Walde zu vernehmen ist, was sicher nicht zur feinen Art (sh. Netiqette im Forum) gehört. Die Ursachen dafür reichen von Gedankenlosigkeit bis hin zur Angst vor der eigenen Courage.
Immerhin soll die Mühe - zwar umsonst - aber nicht vergeblich gewesen sein, diese Gewissheit solltet ihr euren Helfern nicht schuldig bleiben.
Gr
mYthos
|
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 87
Registriert: 07-2003
| | Veröffentlicht am Freitag, den 14. November, 2003 - 21:28: | 
|
ja klar!!
vielen vielen Dank!! auch dass du dir so eine Mühe mit der skizze gemacht hast!!!*freu*
Leider hatte ich noch nicht die zeit mir deine Rechnungen genauer anzugucken
aber wenn ich fertig bin, meld ich mich noch mal, wenn fragen aufkommen und wegen des rests...
|
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 90
Registriert: 07-2003
| | Veröffentlicht am Montag, den 17. November, 2003 - 14:17: | 
|
hallo! hab mir jetzt die Aufgaben angeguckt und soweit keine fragen (glaube ich)
kannst du mir denn noch weiter helfen??
danke |
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 91
Registriert: 07-2003
| | Veröffentlicht am Montag, den 17. November, 2003 - 17:57: | 
|
so, da ist doch noch eine kleine Frage zu a) aufgetaucht
und zwar:
Welche regel steckt hinter der Umformung
e^ln(sqrt(a)) = e^1/2,
die du gleich inder ersten zeile vornimmst?
hierbei:
e^(1/2)*e^d = d*sqrt(a)
hast du doch den ln angewandt oder?
außerdem versteh ich die umformung
[2*sqrt(a)/d]/(a + a/d²) =
2*d²*sqrt(a)/[d*a*(d² + 1)]
nicht! was hast du da gerechnet?
und noch: wie lautet nun die Symmetrieachse? es ist doch nicht die gleiche wie vorher mit x=a oder?
so, dass wars erst mal!
danke schon mal!
VG, Carrie
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 755
Registriert: 03-2002
| | Veröffentlicht am Montag, den 17. November, 2003 - 20:06: | 
|
Hi, zu deinen Fragen
... Welche regel steckt hinter der Umformung
e^ln(sqrt(a)) = e^1/2 ...
Die Definition des Logarithmus bzw. dessen Umkehrung: Wenn man die Basis mit dem Logarithmus einer Zahl potenziert, erhält man wieder diese Zahl:
y = ln(x) «-» e^y = x, d.h. e^(ln(x)) = x
... hierbei:
e^(1/2)*e^d = d*sqrt(a)
hast du doch den ln angewandt oder? ...
Da ist doch tatsächlich ein Fehler meinerseits passiert, der jedoch an der Gleichheit der Funktionswerte an den beiden Stellen nichts ändert. Statt d muss es nämlich e^d heissen!
Aus e^(ln(sqrt(a)) wird deswegen sqrt(a), weil sqrt(a) = a^(1/2), davon der ln ist (1/2)*lna, diesen Wert in die e-Potenz -> [e^ln(a)]^(1/2) = a^(1/2) = sqrt(a).
Also kommt:
e^(ln(sqrt(a) + d) = a^(1/2)*e^d = (e^d)*sqrt(a)
und
e^(ln(sqrt(a) - d) = a^(1/2)/e^d = (1/e^d)*sqrt(a)
[
... außerdem versteh ich die umformung
[2*sqrt(a)/d]/(a + a/d²) =
2*d²*sqrt(a)/[d*a*(d² + 1)]
nicht! was hast du da gerechnet? ...
Den Doppelbruch auf gemeinsamen Nenner d² gebracht, und dann aufgelöst (mit dem Kehrwert des Nenner-Bruches multipliziert)! Das ist jetzt wegen des o.a. Fehlers etwas anders, aber bleibt im wesentlichen gleich:
]
weiter muss es richtig nun so gehen:
....
die entsprechenden Quadrate sind:
a*(e^2d) bzw. a/(e^2d); die Werte für die e-Potenzen nun in fa einsetzen:
fa(ln(sqrt(a) + d) = 2*(e^d)*sqrt(a)/(a + a*(e^2d)) =
= 2*(e^d)*sqrt(a)/[a*((e^2d) + 1)]
und
fa(ln(sqrt(a) - d) = [2*sqrt(a)/(e^d)]/(a + a/(e^2d)) = (auf gemeins. Nenner e^2d)
= 2*(e^d)*sqrt(a)/[a*(e^2d) + a] = 2*(e^d)*sqrt(a)/[a*((e^2d) + 1)]
Wir sehen nun, dass die beiden Funktionswerte gleich sind. Geometrisch bedeutet dies, dass die Funktion bezüglich der Stelle x = (1/2)ln(a) symmetrisch ist (Symmetrieachse ist die Gerade X = ((1/2)ln(a);0) + t*(0;1) bzw. x = (1/2)ln(a)).
... und noch: wie lautet nun die Symmetrieachse? es ist doch nicht die gleiche wie vorher mit x=a oder?
Ich habe dies ja unmittelbar darauf berichtigt, dass nicht x = a die Symmetrieachse ist, hast es überlesen? Es bleibt bei x = (1/2)*ln(a) oder x = ln(sqrt(a)), das ist gleich.
Gr
mYthos
(Beitrag nachträglich am 17., November. 2003 von mythos2002 editiert) |
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 92
Registriert: 07-2003
| | Veröffentlicht am Montag, den 17. November, 2003 - 21:28: | 
|
okay, dann habe ich a) jetzt auch soweit verstanden
hab noch meine Fragen zu b)
"Für den Grenzwert für x -> + oo muss man den Bruch umformen, indem man Zähler und Nenner durch e^(2x) dividiert:
lim(fa)(x -> oo) = lim [(2/e^x) / (a/(e^(2x))+1)"
wie komme ich darauf? Division durch e^2x kann ich irgendwie nicht anwenden...
Nachvollziehen konnt ich ebenfalls nichtden y-Wert:
y = fa_extr = fa(x_extr) = 2*sqrt(a)/(a + a) = 1/sqrt(a)
wie kriege ich im Nenner durch einsetzen von
ln (sqrt(a)) (a+a) heraus??? die Umwandlung danach ist mir auch nicht klar...
bei der Ortskurve wurde der wert des Parameters a doch nur in y eingesetzt (nicht in x) oder habe ich das falsch verstanden?
auf die 2.Ableitung komme ich irgendwie nicht, ich habe es mit der Produkt-und Kettenregel versucht...*verzweifel*
was meinst du mit Vorzeichenfkt.??
Sorry, dass ich noch so viele Fragen stelle, aber ihre Beantwortungeb wären sehr hilfreich!
DANKE
hilfst du mir bitte noch bei 2) weiter?? |
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 95
Registriert: 07-2003
| | Veröffentlicht am Freitag, den 21. November, 2003 - 16:03: | 
|
Mythos??? |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 762
Registriert: 03-2002
| | Veröffentlicht am Samstag, den 22. November, 2003 - 00:53: | 
|
Hi,
die Fragen zu b) vom Montag sind leider nicht in meinen E-Mail Benachrichtigungen gelandet, ich habe sie erst jetzt gesehen.
Wenn du in der gegebenen Funktion
fa(x) = (2*e^x)/(a + e^2x)
Zähler und Nenner NICHT .. dividierst, kommt es beim Einsetzen für x -> oo zum Ausdruck oo/oo, und diesen Wert kannst du nicht bestimmen; man nennt diesen deshalb auch unbestimmte Form. Unbestimmte Formen sind auch Ausdrücke wie 0/0, 0*oo oder oo - oo. Diese müssen für die Grenzwertbestimmung IMMER geeignet umgeformt werden. Hierzu kann auch die Regel von de L'Hospital verwendet werden: Solange unbestimmte Formen der Art 0/0 oder oo/oo vorliegen, können Zähler und Nenner getrennt so lange abgeleitet werden, bis eine eindeutige Form entsteht.
Hier sieht das dann so aus:
lim[x -> oo]fa(x) = lim[x -> oo][(2*e^x)/(a + e^2x)] =
lim[x -> oo][(2*e^x)/(2*e^2x)] =
lim[x -> oo][(1/(e^x)] = 1/oo = 0
Falls diese Regel noch nicht Stoff sein sollte, musst du eben Zähler und Nenner entweder durch e^x oder durch e^(2x) dividieren; auch die Division durch e^x führt schon zum Erfolg. Bei der Division durch Potenzen (die du nicht anwenden kannst??) sind lediglich die Potenzgesetze zu beachten. Die Division durch e^x (ist eventuell leichter):
lim[x -> oo][(2*e^x)/(a + e^2x)] =
lim[x -> oo][(2/(a/e^x + e^x)] = 2/(0 + oo) = 2/oo = 0
Zum Funktionswert an der Stelle x = (1/2)*ln(a):
Wenn x = (1/2)ln(a), ist e^(2x) = e^(ln(a)) = a
e^x ist dann die Wurzel daraus, also sqrt(a). Dies alles in fa(x) einsetzen, ergibt eben:
fa(x) = (2*e^x)/(a + e^2x)] = 2*sqrt(a)/(a + a) =
2*sqrt(a)/(2a) = [sqrt(a)]/a = 1/sqrt(a)
Zur Ortskurve:
Es werden klarerweise BEIDE Gleichungen, also die für x UND die für y für die Eliminierung des Parameters a herangezogen!
1. x = (1/2)*ln(a)
2. y = 1/sqrt(a)
-------------------
Aus 1:
2x = ln(a)
a = e^(2x)
Nun in 2., wo die Abhängigkeit des y von a steht, statt a den Wert e^(2x) einsetzen:
y = 1/sqrt(a), sqrt(a) = e^x ->
y = 1/e^x = e^(-x)
Es wurde also der Wert des Parameters a, ausgedrückt in x (!) in y = .. eingesetzt.
Die Ortskurve für alle durch Variation von a entstehenden Extremwerte lautet daher:
y = e^(-x)
°°°°°°°°°°
Jetzt klar?
Die Vorzeichenfunktion sgn(x) gibt eigentlich den Wert +1 für positive x und -1 für negative x aus. Gemeint war, dass für das Extremum nur das Vorzeichen, aber nicht der Wert der zweiten Ableitung maßgeblich ist.
Teil 2 folgt
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 763
Registriert: 03-2002
| | Veröffentlicht am Samstag, den 22. November, 2003 - 00:54: | 
|
(Teil 2)
Für den Wendepunkt ist die 2. Ableitung korrekt zu ermitteln!
fa'(x) = 2*(e^x)*(a - e^(2x))/(a + e^(2x))²
Die 2 vor die Ableitung, wieder mit der Produkt-, Bruch- und Kettenregel, Ausklammern von e^x und Kürzen durch (a + e^(2x)):
fa''(x) = 2*e^x*(a² - 6a*e^(2x) + e^(4x))/(a + e^(2x))³
fa''(x) = 0, der einzige Faktor, der Null werden kann, ist
a² - 6a*e^(2x) + e^(4x) = 0, biquadratisch
Substitution: Setze e^2x = z, ->
z² - 6az + a² = 0
z1,2 = 3a +/- sqrt(9a² - a²) = a*(3 +/- sqrt(8))
Rückeinsetzen in Subst.:
e^(2x) = a*(3 +/- sqrt(8))
x = (1/2)*ln[a*(3 +/- sqrt(8))]
Wie man sich durch Rationalmachen des Nenners überzeugen kann, ist
3 + sqrt(8) = 1/(3 - sqrt(8))
und die Logarithmen der beiden Zahlen unterscheiden sich daher nur durch das Vorzeichen!
ln[1/(3 - sqrt(8))] = - ln(3 + sqrt(8))
Somit
x1 = (1/2)*ln(a) + (1/2)*ln(3 + sqrt(8))
x2 = (1/2)*ln(a) - (1/2)*ln(3 + sqrt(8))
bzw.
x1 = (1/2)*ln(a) + 0,881374
x2 = (1/2)*ln(a) - 0,881374
Die beiden Wendepunkte liegen wieder symmetrisch zur Geraden x = (1/2)*ln(a), das kannst du auch aus der Grafik ersehen!
y1 und y2 ergeben sich durch Einsetzen der x-Werte in fa(x):
y1 = 2*sqrt(a)*sqrt(3 + sqrt(8))/[a*(4 + sqrt(8))] = 1/sqrt(2a)
für a = 1 beispielsweise ist y1 = 1/sqrt(2) = 0,707107
Die Steigung der Wendetangente durch Einsetzen in die erste Ableitung:
fa'(x) = 2*(e^x)*(a - e^(2x))/(a + e^(2x))²
m1 = fa'(x1) =
= 2*sqrt(a)*sqrt(3 + sqrt(8))*(-2 - sqrt(8))*a/[a²*(4 + sqrt(8))²] = ... =
= 1/(2*(sqrt(a))
für a = 1 beispielsweise ist die Steigung m1 = 1/2
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Bei 2. musst du mir bitte sagen, welches die Funktion ft ist, diese muss angegeben sein ...
Gr
mYthos
|
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 98
Registriert: 07-2003
| | Veröffentlicht am Samstag, den 22. November, 2003 - 22:40: | 
|
Erst mal DANKE, dass du dich wieder gemeldet hast!!!!!
ich hab noch ne kleine Frage zu a)
und zwar warum kann die Gerade auch als
Gerade X = ((1/2)ln(a);0) + t*(0;1) dargestellt werden
wo kommen 0 und 1 her? sind die ersten koordinaten der Aufhängepunkt?
bei b)kenne ich die Regel des L´Hospitals aber frag ich mich ob nicht der unbestimmte Ausdruck 0/0 entsteht und nicht oo/oo, da doch e^+/-oo immer null ist!?
und muss das Intervall nicht offen sein??? wie kommt man überhaupt auf die Monotiebereiche???
mfg Carrie |
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 99
Registriert: 07-2003
| | Veröffentlicht am Samstag, den 22. November, 2003 - 22:43: | 
|
achso, zur Funktin f(t): die ist nicht angegeben!
ich habe mich auch schon gewundert, aber es steht nur f1(t)dt, also mit a= 1 und t sozusagen als Variabel (anstatt x)
hilft dir das weiter? |
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 263
Registriert: 10-2003
| | Veröffentlicht am Samstag, den 22. November, 2003 - 23:25: | 
|
Hi Carrie,
Mythos hat die Gerade mit der Gleichung
x = (1/2)ln(a),
die ja eine Parallele zur y-Achse ist, in der Schreibweise der analytischen Geometrie bzw. der Vektorrechnung dargestellt. Die Gerade verläuft ja durch alle Punkte mit dem x-Wert x = (1/2)ln(a), also auch durch ((1/2)ln(a);0) und da sie parallel zur y-Achse verläuft, ist ihr Richtungsvektor (0;1) (0 Schritte in x-Richtung, 1 Schritt in y-Richtung).
Alles klar?
Mit freundlichen Grüßen
Jair
|
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 264
Registriert: 10-2003
| | Veröffentlicht am Samstag, den 22. November, 2003 - 23:28: | 
|
Zu deiner 2.Frage:
e-¥ ist 0, e+¥ ist aber ¥.
Eigentlich gibt es die Ausdrücke oben gar nicht, sondern nur die Grenzwerte, aber ich hoffe, du weißt, was ich meine.
Mit freundlichen Grüßen
Jair
|
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 265
Registriert: 10-2003
| | Veröffentlicht am Samstag, den 22. November, 2003 - 23:51: | 
|
Die Aufgabe 2) bezieht sich auf dieselbe Funktionenschar, die schon in Aufgabe 1) benutzt wurde. Da hier ja eine Integralfunktion mit der oberen Grenze x als Funktionsvariable vorliegt, wird für die Integrationsvariable natürlich ein anderer Buchstabe (hier t) benutzt.
Die Rechnung läuft so:
F(x)=ò0 xf1(t)dt
= ò0 x(2et)/(1+e\+(2t))dt
= 2ò1 exdz/(1+z²) bei der Ersetzung z=et, dz=etdt
= 2 arctan et|0x
= 2 arctan ex - 2 arctan 1
= 2 arctan ex - 2*p/4
= 2 arctan ex - p/2
Mit freundlichen Grüßen
Jair
|
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 266
Registriert: 10-2003
| | Veröffentlicht am Sonntag, den 23. November, 2003 - 00:00: | 
|
Auch der 1.Teil von a) ist einfach: Damit F streng monoton steigend ist, muss ja nur gelten:
F'(x)=f1(x)>0.
Nun ist aber 2ex>0 und 1+e2x ebenfalls immer positiv. Das war's.
Zur Symmetrie fällt mir im Augenblick nichts ein, und für die Aufgaben b und c bin ich heute Nacht zu müde. Vielleicht geht's morgen weiter.
Mit freundlichen Grüßen
Jair
|
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 101
Registriert: 07-2003
| | Veröffentlicht am Sonntag, den 23. November, 2003 - 14:20: | 
|
hey Jair Ohmsford, dass ist ja supernett, dass du mir jetzt auch noch weiterhilfest!!!!  das freut mich; ich hab deine Erklärungen auch verstanden. das freut mich; ich hab deine Erklärungen auch verstanden.
jetzt weiß ich auch was mit ft gemeint ist!
wie sieht das noch mit dem Intervall aus???
DANKE
mfg |
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 102
Registriert: 07-2003
| | Veröffentlicht am Sonntag, den 30. November, 2003 - 18:40: | 
|
hallo
weiß denn nun jemand, warum das Intervall einmal +oo und ein mal
-oo hat???
wie ist das mit der Symmetrie zum Ursprung???
@Mythos: die Wendepunktberechnung stimmt glaube ich nicht, denn das soll ja für F(x) gelten...
Habe da jedenfalls ne andere Lösung auf einem Lösungszettel stehen.
Daher brauche ich auch keine Hilfe mehr beim Rest.
Wäre trotzdem nett, die obigen Fragen noch mal beantwortet zu bekommen.
Hoffe ihr habt noch Lust dazu!?
danke |
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 298
Registriert: 10-2003
| | Veröffentlicht am Sonntag, den 30. November, 2003 - 21:49: | 
|
Hallo Carrie,
gar nicht einfach, den Bezug deiner Fragen in dem langen Thread wieder zu finden. Ich hoffe, es ist mir gelungen. Weil es so schwer ist, die getippten Terme zu lesen, gebe ich dir die Antworten hier handgeschrieben, Zunächst die Frage nach den Grenzwerten:
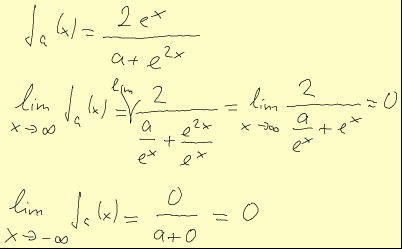
Man kürzt (für den lim x->¥) also den ganzen Bruch durch ex. Dabei fällt ex im Zähler weg. Im Nenner erhält man halt den Term a/ex und ex. Nun bleibt der Zähler konstant, während der Nenner über alle Grenzen geht. Der Grenzwert ist also 0.
Für x->-¥ ist es noch einfacher. 2ex geht dann nämlich gegen 0. e2x auch, a aber nicht. Also ist der Grenzwert einfach 0/(a+0) = 0.
Nun zur Frage der Monotonie. Man erhält die Monotoniebereiche, indem man nach dem Vorzeichen der 1. Ableitung fragt. Diese 1. Ableitung hat die Gleichung:
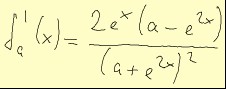
Nun kann der Nenner nicht negativ werden, 2ex im Zähler auch nicht. Alles hängt also nur an der Klammer (a-e2x). Diese kann 0 werden, nämlich für e2x=a, d.h. x=(1/2)ln a, wie Mythos schon gezeigt hat.
Nun ist e2x eine streng monoton steigende Funktion. Demnach muss e2x<a sein für x<(1/2)ln a, und e2x>a sein für x>(1/2)ln a. Damit ist die Klammer positiv für x<(1/2)ln a ("links" vom Maximum, wie Mythos so anschaulich schrieb) und negativ für x>(1/2)ln a ("rechts" vom Maximum). Die Funktion ist also streng mononton steigend für x<(1/2)ln a und zwar für alle solche x, sozusagen von -¥ an. Daher die Schreibweise ]-¥;(1/2)ln a[.
Entsprechend ist die Funktion streng monoton fallend für x>(1/2)ln a, also für ](1/2)ln a;¥[.
Wieso hat Mythos das abgeschlossene Intervall benutzt? Nun, an der Grenze (1/2)ln a geht das streng monotone Steigen gerade ins streng monotone Fallen über. Dieser Punkt gehört also zu beiden Bereichen und sollte tatsächlich beide Male mit eingeschlossen werden. Dagegen würde ich die "Punkte" ±¥, die ja in Wirklichkeit gar nicht als Zahlen existieren, nicht in das Intervall hineinnehmen. Die bessere Schreibweise - wenn man sie denn überhaupt benutzen will - ist m.E. also ]-¥;(1/2)ln a] und [(1/2)ln a;¥[
Zu guter Letzt:
Eine Symmetrie zum Ursprung liegt nicht vor, sonst müsste 2ex/(a+e2x) ja irgendwo negativ sein. Es gibt lediglich die von Mythos beschriebene Achsensymmetrie bzgl. der Geraden x=(1/2)ln a.
So, ich hoffe, ich konnte deine Fragen nun zu deiner Zufriedenheit beantworten. Wie gesagt - langsam wird's unübersichtlich 
Aber wenn noch etwas unklar ist, melde dich ruhig nochmal.
Mit freundlichen Grüßen
Jair
|
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 104
Registriert: 07-2003
| | Veröffentlicht am Montag, den 01. Dezember, 2003 - 15:09: | 
|
so, danke Jair für deine Hilfe und Mühe!
Nun sind alle unklarheiten beseitigt!!!
mit den Intervalen ist das so ne Sache... auf dem lösungszettel sind sie jedenfalls auf beiden seiten offen, aber egal!
Ach und die Symmetrie zum Ursprung bezog sich übrigens auf Aufgabe 2a), der Graph F soll dies nämlich sein!
ich weiß es ist schon etwas unübersichtlich..
aber vllt. kannst du mir hier noch ein letztes Mal mit der SYmmetrie helfen und das solls dann sein!!!
danke |
    
Jair_ohmsford (Jair_ohmsford)

Erfahrenes Mitglied
Benutzername: Jair_ohmsford
Nummer des Beitrags: 311
Registriert: 10-2003
| | Veröffentlicht am Montag, den 01. Dezember, 2003 - 16:07: | 
|
Hi Carrie!
Die Punktsymmetrie der Funktion F ist sehr schön zu zeigen:
Zunächst einmal ist f1(x)=(2et)/(1+e2t) achsensymmetrisch zu x=1/2 * ln 1 = 0. Das ist aber die y-Achse. Es gilt also f(-x)=f(x), d.h. (2et)/(1+e2t)=(2e-t)/(1+e-2t)
Nun rechnen wir mal los:
F(-x)
=ò0 -x((2et)/(1+e2t)dt
= ò0 -x(2e-t)/(1+e-2t)dt (wegen der Achsensymmetrie)
*** Hier ersetzen wir nun z = -t, dz = -dt. ***
= -ò0 x (2ez)/(1+e2z)dz
= -F(x) q.e.d.
Mit freundlichen Grüßen
Jair
|
    
Carrie (Carrie)

Erfahrenes Mitglied
Benutzername: Carrie
Nummer des Beitrags: 105
Registriert: 07-2003
| | Veröffentlicht am Montag, den 01. Dezember, 2003 - 18:18: | 
|
hey Jair!
danke, jetzt ist alles komplett!
nach 30 Einträgen
mfg carrie |