| Autor |
Beitrag |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 806
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 18. Juli, 2003 - 21:58: | 
|
Es folgt eine nette Aufgabe, die-wie ich finde- wohl unseren hohen Anspruch entspricht.
Gegeben sei das gleichseitige Dreieck ABC mit der Seitenlänge a. Auf der Höhenlinie hc liegen zwei Kreise k1 und k2 so übereinander, das sie sich in einem Punkt berühern. Der Kreis k1 tangiert darüberhinaus die Seiten AC und BC des gleichseitigen Dreiecks.
Ein dritter Kreis k3 liegt auf der Verbindungslinie MB, wobei der Punkt M den Umkreismittelpunkt markiert. Der Kreis k3 tangiert die Seiten AB und BC.
Gibt es einen Kreisradius für k3 so, daß er genau die beiden anderen Kreise in je einem Punkt berühert?
Wenn ja, so berechnen Sie die Kreisradien r1, r2 und r3 in Abhängigkeit von a für diesen Fall!
viel Spaß beim Knobeln!
mfg
Niels
|
    
Georg (georg)

Erfahrenes Mitglied
Benutzername: georg
Nummer des Beitrags: 140
Registriert: 08-2000
| | Veröffentlicht am Samstag, den 19. Juli, 2003 - 06:55: | 
|
Ich frage mich, ob ich etwas falsch verstanden habe, denn ich komme auf unendlich viele Lösungen. Deswegen lege ich ein Beispiel bei :
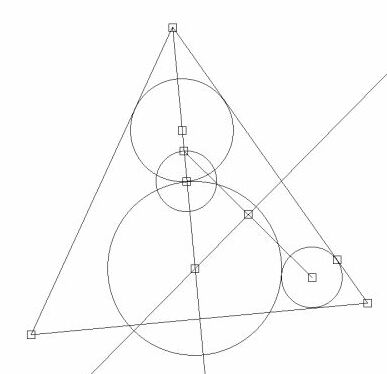 |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 807
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 19. Juli, 2003 - 09:26: | 
|
Hi Georg,
vieleicht soviel zur Information:
Der Kreis k2 berührt die Kreise k1 und k3 sowie die Strecke AB=a in einem Punkt.
Da bei diener obigen Skizze Bezeichnungen fehlen kann ich leider wenig damit Anfangen.
Es existieren feste Beziehungen zwischen den Radien r1,r2,r3 und der allgemeinen Seitenlänge a.
Wer findet die 3 Gleichungen?
Gruß
Niels |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 808
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 19. Juli, 2003 - 09:30: | 
|
Achso, mit Umkreismittelpunkt M ist natürlich der Umkreismittelpunkt des Dreiecks ABC gemeint. aber in diesem Sonderfall ist er ja bekanntlich "Mehr als nur ein Umkreismittelpunkt".
mfg
Niels |
    
Georg (georg)

Erfahrenes Mitglied
Benutzername: georg
Nummer des Beitrags: 142
Registriert: 08-2000
| | Veröffentlicht am Samstag, den 19. Juli, 2003 - 11:23: | 
|
Danke, jetzt ist alles klar.
k2 berührt ... die Strecke AB=a
hat meiner Meinung nach in der Aufgabenstellung gefehlt. |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 809
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 19. Juli, 2003 - 11:50: | 
|
Dann sind ja alle Unklarheiten beseitigt.
viel Spaß beim knobeln!
Gruß N.
|
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 812
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 20. Juli, 2003 - 08:08: | 
|
Noch keine Idee Freunde?
vieleicht solltet ihr es ja mal mit den guten alten Pythagoras versuchen.
mfg
Niels |
    
Georg (georg)

Erfahrenes Mitglied
Benutzername: georg
Nummer des Beitrags: 145
Registriert: 08-2000
| | Veröffentlicht am Sonntag, den 20. Juli, 2003 - 10:40: | 
|
3 Gleichungen für die drei Radien habe ich. Leider hat meine Auflösung eine Gleichung vierten Grades ergeben, so dass ich keine Probe machen kann, sondern mindestens noch einmal rechnen muss. |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 813
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 20. Juli, 2003 - 11:19: | 
|
Ich bin gespannt auf dein Ergebnis Georg!

mfg
Niels |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 817
Registriert: 06-2001
| | Veröffentlicht am Montag, den 21. Juli, 2003 - 10:58: | 
|
Wenn bis heute Abend niemand eine Lösung Vorschlägt, werde ich die Lösung präsentieren.
Der Countdown läuft.
fröhliches schaffen!
mfg
Niels |
    
Georg (georg)

Erfahrenes Mitglied
Benutzername: georg
Nummer des Beitrags: 148
Registriert: 08-2000
| | Veröffentlicht am Montag, den 21. Juli, 2003 - 12:19: | 
|
Teillösung :
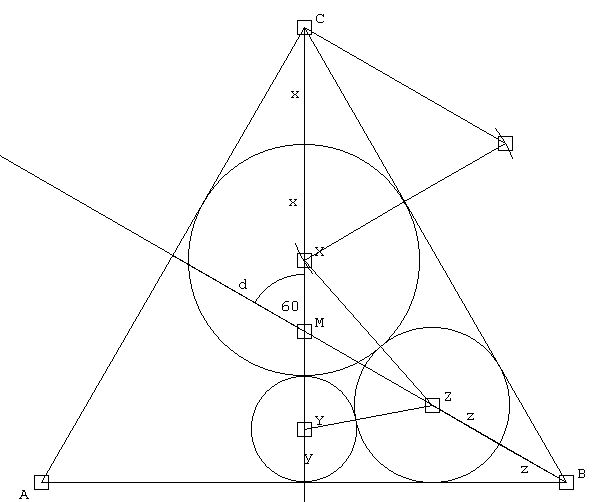
Bei mir heißen die Kreise X, Y und Z, weil ich zu faul bin, Indizes zu schreiben. Rechts oben zeigt eine kleine Vorüberlegung, dass die Kreise X und Z in den 60°-Winkeln genau den doppelten Radius von den Ecken C und B entfernt sind.
Die Dreieck-Seitenlänge a taucht nur in Gestalt einer Substitution auf,
d = 1/6 * Wurzel(3) * a .
Auf der Höhe auf c kann man sehen :
3d = 3x + 2y
Im Dreieck MYZ führt der Cosinus-Satz nach Vereinfachung auf :
4yz = 3 * ( d² + z² - 2dz )
Im Dreieck XMZ führt der Cosinus-Satz nach Vereinfachung und Auflösen nach x auf :
x = 1/3 * ( 6d - z +- 2 * Wurzel(6dz-2z²) )
Die letzten beiden Gleichungen setze ich in die erste und erhalte :
11z^4 - 32dz³ + 2d²z² + 3d^4 = 0 und dazu fällt mir bis jetzt nichts mehr ein. |
    
Georg (georg)

Erfahrenes Mitglied
Benutzername: georg
Nummer des Beitrags: 150
Registriert: 08-2000
| | Veröffentlicht am Dienstag, den 22. Juli, 2003 - 12:33: | 
|
mit w = z/d lässt sich der Überblick ein wenig verbessern :
11w^4 + 2w² + 3 = 32w³ |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 819
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 22. Juli, 2003 - 13:16: | 
|
Hallo allerseits,
es folgt die versprochene Auflösung der Aufgabe KB Nr. 22:
Methode 1: Satz des Pythagoras
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Teil 1 der Auflösung:
===========================
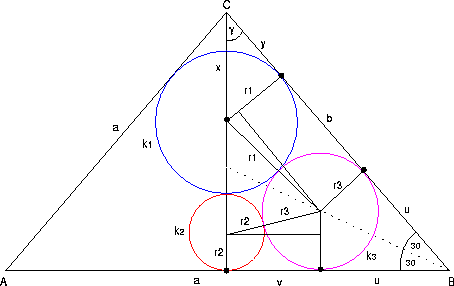
Im ersten Schritt berechnen wir die Strecken x und y am Kreis k1:
sin(c)=r1/x
Da c=30° folgt daraus:
x=2r1
und für
tan(c)=r1/y
ergibt sich:
y=r1*sqrt(3)
Betrachten wir nun die Höhe h im gleichseitigen Dreieck. Nachdem die Strecke x bekannt ist können wir eine Gleichung zwischen den Radien r1, r2 und h notieren:
gl1: h=0,5*a*sqrt(3)=x+r1+2r2=3r1+2r2
Ähnlich können die Teilstrecken u, v auf der Seite AB berechnet werden.(Wie groß ß ist könnt ihr euch ja denken...)
tan(ß)=r3/u
u=r3*sqrt(3)
u+v=0,5a
->v=0,5a-r3*sqrt(3)
Schließlich folgt für die Teilstrecke b auf der Seite BC :
b=a-u-y=a-r3*sqrt(3)-r1*sqrt(3)
Nun fällen wir das Lot vom Mittelpunkt des Kreises k3 auf den jeweils gegenüberliegenden Radius r2 bzw. r3. Mit dem Satz des Pythagoras folgt :
gl2: b²+(r1-r3)²=(r1+r3)²
gl3: v²+(r3-r2)²=(r2+r3)²
Die Größen b, v werden durch die entsprechenden Gleichungen ersetzt. Mit der Beziehung gl1 haben wir eine dritte unabhängige Beziehung zwischen den gesuchten Kreisradien und der gegebenn Dreiedksseitenlänge a. Zu lösen ist nun das Gleichungssystem gl1.gl2,gl3.
Wer traut sich dieses Gleichungssystem zu lösen? Kleiner Tipp: Mann könnte auch zu not ein Computeralgebrasystem wie Marple zur Lösung heranziehen....
Der zweite Teil der Lösung ist nun wieder den fleißigen Rechnern überlassen und folgt ggf. später!
=======================================
mfg
Niels |