| Autor |
Beitrag |
    
H.R.Moser,megamath (megamath)

Senior Mitglied
Benutzername: megamath
Nummer des Beitrags: 2221
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 10. Juli, 2003 - 09:13: | 
|
Hi allerseits,

Dreiecksaufgabe 8.
Von einem Dreieck kennt man die Winkel
alpha = 60° und beta = 45°
Berechne die folgenden sechs Quotienten (exakte Werte):
q1=a/(b+c), q2=b/(c+a), q3=c/(a+b)
q1=a/(b-c), q2=b/(c-a), q3=c/(a-b).
MfG
H.R.Moser,megamath
|
    
*** (hydra)

Mitglied
Benutzername: hydra
Nummer des Beitrags: 20
Registriert: 06-2003
| | Veröffentlicht am Freitag, den 11. Juli, 2003 - 09:28: | 
|
Verwende den Sinus Satz:
a = c sina / sin(a+b) , b = c sinb /sin(a+b)
sin 60° = Ö(3)/2 , sin 45° = Ö(2)/2 , sin 105° = (Ö(6)+Ö(2))/4
(Beitrag nachträglich am 11., Juli. 2003 von hydra editiert)

|
    
H.R.Moser,megamath (megamath)

Senior Mitglied
Benutzername: megamath
Nummer des Beitrags: 2224
Registriert: 07-2002
| | Veröffentlicht am Freitag, den 11. Juli, 2003 - 10:35: | 
|
Hi ***(hydra),

Vielen Dank für Deine Bemühungen zur Lösung
dieser Aufgabe.
Sie war eher leicht und der Sinussatz drängt sich
geradezu auf. Man kann sich sogar ein Bild verschaffen.
Dazu dienen die Skizzen, welche zur konstruktiven Lösung
der Aufgaben mit der Seitensumme b + c gemacht werden.
Bei der Konzeption der Aufgabe dachte ich allerdings an
etwas ganz anderes, nämlich an die Mollweideschen Formeln,
die man heutzutage gar nicht mehr zur Kenntnis nimmt;
sie lauten:
q1=a/(b+c) = sin[½ alpha] / cos[½(beta-gamma)]
q2=b/(c+a) =…… durch zyklische Vertauschung
q3=c/(a+b) =…… durch zyklische Vertauschung
q4=a/(b-c) = cos[½ alpha] / sin[½(beta-gamma)]
q5=b/(c-a) =…… durch zyklische Vertauschung
q6=c/(a-b) =…… durch zyklische Vertauschung
Zum Beweis der ersten Formel:
Nach dem Sinussatz (sic) ist
a = 2 r sin(alpha), b = 2r sin (beta) c = 2r sin (gamma),
also
a/(b+c) = sin (alpha) / [sin (beta) + sin (gamma)]
Umformung des Zählers rechts zu
2 sin (½ alpha) cos (½ alpha),
Umformung des Nenners rechts zu
2 sin [½(beta+gamma)] cos [½(beta-gamma)]
Wegen des Winkelsummensatzes gilt
sin [½(beta+gamma)] = cos(½ alpha):
Daraus entsteht schließlich die erste Mollweidesche Formel.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 773
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 11. Juli, 2003 - 10:54: | 
|
Hi Megamath,
du hast ja die Mollweidschen Formeln auf mehr analytischen Wege formal über den Sinussatzbewiesen bewiesen.
Wenn ihr lust habt könnte ich eine geometriesche Interpretation der "Mollweidschen Formeln" liefern. Sozusagen ein geometrischer Beweis.
Wenn interesse besteht publiziere ich ihn hier.
Gruß N. |
    
H.R.Moser,megamath (megamath)

Senior Mitglied
Benutzername: megamath
Nummer des Beitrags: 2225
Registriert: 07-2002
| | Veröffentlicht am Freitag, den 11. Juli, 2003 - 10:59: | 
|
Hi Niels,
Gerne,mach das !
MfG
H.R.Moser,megamath |
    
*** (hydra)

Mitglied
Benutzername: hydra
Nummer des Beitrags: 21
Registriert: 06-2003
| | Veröffentlicht am Freitag, den 11. Juli, 2003 - 11:25: | 
|
Hallo Megamath!
Ja, der tiefere Sinn dieser Aufgabe war mir vorerst verborgen. Die Mollweideschen Formeln kamen mir nicht in den Sinn. In einem alten "Lehrbuch der Elementar-Geometrie" von Julius Henrici und Peter Treutlein aus dem Jahre 1891 habe ich auch noch die Bezeichnung "Cagnolische Formeln" gefunden (ich versuche ein Bild einzufügen)
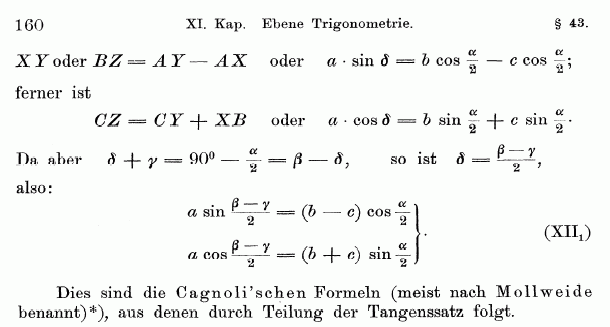
Dazu eine persönliche Frage aus historischem Interesse: Ich nehme an, dass du den ETH-Professor Peter Henrici persönlich gekannt hast. Weißt du zufällig, ob Julius (1841-1910) sein (Ur)Großvater war?
@Niels: Geometrische Beweise interessieren mich ganz besonders!

|
    
H.R.Moser,megamath (megamath)

Senior Mitglied
Benutzername: megamath
Nummer des Beitrags: 2226
Registriert: 07-2002
| | Veröffentlicht am Freitag, den 11. Juli, 2003 - 13:05: | 
|
Hi ***(hydra),
Mollweide (1774-1825) ist vor allenm durch
die von ihm gefundene flächentreue Kartenprojektion bekannt.
Er hat 1808 die nach ihm benannten Formeln,
die schon 101 Jahre früher von Newton gefundenen
worden waren,wieder entdeckt.
Gauss hat(1809)auf die Bedeutung dieser Formeln
hingewiesen.
Daher werden die Formeln in manchen Arbeiten
als Gauss -Mollweidesche Formeln bezeichnet.
Spannend wird die Angelegenheit in der sphärischen Trigonometrie.
Dort gibt es keinen Winkelsummensatz,
und die Seiten treten in der Geatalt von Winkeln auf.
Die Gauss-Mollweideschen Formeln erscheinen
in modifizierter Gestalt.
Zu Deiner Frage nach Peter Henrici.
Ich habe mit ihm an der ETH studiert
(mit wenigen JahrenZeitdifferenz),
und ich habe später seine Leistungen
auf den verschiedensten Fachgebieten der Mathematik schätzen gelernt.
Ueber die von Dir erwähnten allfälligen verwandtschaftlichen Beziehuingen
zum Buchautor ist mir nichts bekannt.
MfG
H.R.Moser,megamath
|
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 774
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 11. Juli, 2003 - 14:51: | 
|
Hi Megamath und hydra,
wie gewünscht kommt hier ein "geometrischer Beweis" der Mollweidschen Formeln:
Beweis der Mollweidschen Formeln:
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
[skizzenbeschreibung:]
Wir zeichnen ein normales Dreieck ABC.Die Strecken sind wie immer AB=c,BC=a,AC=b, wobei allerdings gelten soll b<a oder besser gesagt a>b gelten soll. Die Winkel sind wie üblich mit a,b,c zu bezeichnen.
Wir zeichnen weiter ein Kreis k um C mit Radius b.Dieser Kreis k schneidet die über C hinaus verlängerte Strecke CB in zwei Punkten D1 und D2.
Es gilt:
Strecke D1B=a+b
Strecke D2B=a-b
Das Dreieck D1AC ist gleichschenklig(Schenkel b).
Es gilt:
Winkel CD1A= Winkel D1AC
Ferner gilt:
Winkel D1AC=180°-c
Weil, Winkel BCA=c
180°=180°-c+2*winkel CD1A
Eine kurzweilige Rechnung ergibt:
Winkel CD1A=Winkel D1AC=c/2
Weiter gehts:
Wegen des Satzes von Thales muss gelten:
Winkel CAD2+Winkel D1AC=90°
Winkel CAD2+c/2=90°
2*Winkel CAD2=180°-c
2*Winkel CAD2=a+b
WinkelCAD2=(a+b)/2
Das Dreieck AD2C ist ebenfalls gleichschenklig(schenkel b). Deswegen gilt:
Winkel CD2A=(a+b)/2
Nun schauen wir uns das Dreieck ABD2 an.
Es gilt:
Winkel D2AB=Winkel CAB -Winkel CAD2
Winkel D2AB=a-(a+b)/2
Eine Ebenfalls kurzweilige Rechnung hat zum Ergebnis:
WinkelD2AB=(a-b)/2
Damit wissen wir nun im Grunde alles, was wir wissen wollen:
Wir wenden auf das Dreieck D2AB den Sinussatz an:
BD1/AB=sin{90°+(a-b)/2)/sin(c/2)
Nun weis man ja, das aus Symetriegründen bei der Sinusfunktion gilt:
sin(90°+(a-b)/2)=sin(90°-(a-b)/2)=cos((a-b)/2)
Und somit ergibt sich die gute alte Mollweidsche Formel:
BD1/AB=cos((a-b)/2)/sin(c/2)
Die weiteren Mollweidschen Formeln bekommt man entweder durch zyklisches Vertauschen oder man ändert die Skizze etwas ab . .
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Anmerkung:
Mit der gleichen Überlegungsfigur und ein parr weiteren kleinigkeiten kann man auch den "Tangenssatz" beweisen. Ein Satz der heutzutage ebenfalls in der Schule keine Rolle mehr spielt! . .
Ich hoffe der Beweis ist nachvollziebar!
mfg
Niels |
    
*** (hydra)

Mitglied
Benutzername: hydra
Nummer des Beitrags: 22
Registriert: 06-2003
| | Veröffentlicht am Freitag, den 11. Juli, 2003 - 17:41: | 
|
Hallo!
@Megamath
Ich habe vor allem Henricis exzellente Arbeiten zur Numerischen Mathematik kennen und schätzen gelernt.
Seit deiner kürzlich gemachten Bemerkung über Polyas Vorlesungen war mir klar, dass du gemeinsam mit Henrici studiert haben musst. Vielen Dank für deine Erläuterungen!
@Niels
Ein sehr gut verständlicher Beweis!

|
|