| Autor |
Beitrag |
    
Maugo

| | Veröffentlicht am Dienstag, den 19. Februar, 2002 - 18:45: | 
|
Ist diese Funktion nicht göttlich????
Ha,wenn ich da mal nicht lache..........Ich hab absolut keine Ahnung, wie man diese Funktion f(x)=ln(lnx) lösen soll.
Und zwar sollen wir die Nullstellen berechen, den Schnittwinkel mit der x-Achse, den Definitions-und Wertebereich und natürlich die Wendepunkte.............Kann mir da vielleicht jemand helfen? Hab ehrlich nen großen Defizit bei solchen Funktionen.....*schnief*
Maugo*traurigschau* |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Dienstag, den 19. Februar, 2002 - 21:34: | 
|
vielleicht bin ich zu naiv
aber formell sind die Ergebnisse folgende:
Nullstelle
ln(ln(x)) = 0
eln(x)=1 weil e°=1
x = 1
Ableitung nach Kettenregel
f' = 1/(x*ln(x)) also Schnittwinkel mit x-Achse
tg(Schnitt) = 1/(1*ln(1)) "=" unendlich,
Winkel = 90°
Wendepunkt:
f''= (x*ln(x))'/(x²ln²x) = (ln(x)+x/x)/(x²ln²x)
f''= (1+ln(x))/(x²ln²x)
f'' = 0 für x = e-1
es gibt, für reelle x, keinen Wendepunkt, f(e-1)=ln(-1)
Def.Ber: 1..Unendlich, Wertber.: 0..Unendlich |
    
K.

| | Veröffentlicht am Mittwoch, den 20. Februar, 2002 - 19:36: | 
|
Hallo Maugo, hallo Friedrich
ich komme zu folgenden Ergebnissen
f(x)=ln(lnx)=0
<=> e0=lnx
<=> 1=lnx
<=> e1=x
<=> x=e
=> N(e|0) ist Nullstelle
Mit f'(x)=1/(xlnx) folgt
f'(e)=1/(e*lne)=1/e=tana
=> a=20,2° ist der Schnittwinkel
Wendestellen gibt es keine
Definitionsbereich ist D={x€R|x>1}
Wertebereich W=R
Mfg K. |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Donnerstag, den 21. Februar, 2002 - 11:03: | 
|
Hallo K.,1 Bild sagt mehr ...
damit überprüfbar (dass log wirklich ln und die rote Kurve wirklich ln(ln(x)) ist hab ich noch 2 Konstanten eingezeichnet:
grün: log(exp(1)) also ln(ex)
blau: exp(1) also ex
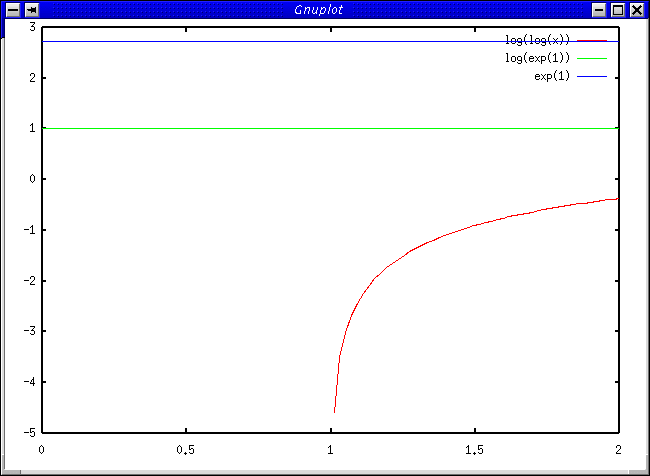
Gruss
F. |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Freitag, den 22. Februar, 2002 - 13:48: | 
|
autsch,
eigenen Plot missinterpretiert, nicht gesehen wo
f(x)=0 |
|