| Autor |
Beitrag |
    
Baggy (baggy)

Neues Mitglied
Benutzername: baggy
Nummer des Beitrags: 4
Registriert: 02-2003
| | Veröffentlicht am Montag, den 03. März, 2003 - 16:35: | 
|
ja ich soll die größmöglichen Definitionsbereich errechnen
weiß jedoch nicht wirklich wie das funktionieren soll
f(x)= 3/x-2
f(x)=6/-x+3
f(x)= x²+3x-4/x-2
f(x)= x²+5x+6/x²
es wäre echt super wenn ihr mir dabei helfen könnt. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 982
Registriert: 02-2002
| | Veröffentlicht am Montag, den 03. März, 2003 - 16:37: | 
|
Hi Baggy
Ich schätze mal du hast ein paar Klammern vergessen. Aber grundsätzlich geht es bei deinen Aufgaben nur darum herauszufinden, wann ein Nenner Null wird. Genau an den Stellen ist dann die Funktion nicht definiert, sonst an allen.
MfG
C. Schmidt |
    
Baggy (baggy)

Neues Mitglied
Benutzername: baggy
Nummer des Beitrags: 5
Registriert: 02-2003
| | Veröffentlicht am Montag, den 03. März, 2003 - 19:18: | 
|
ein mom ich schreibe mal die ganze aufgabe auf.
Ermittel sie den größtmöglichen Definitionsbereich der folgenden durch ihre Funktionsterme gegebenen Funktionen in IR sowie das Symmetrieverhalten ihrer Graphen.
Bestimmen Sie sowohl die Art der Definitonslücken als auch die Art der Asymptoten. Von welcher Seite nähren sich die einzelnen Graphen ihren Asymptoten?
Berechenen sie die Achsenschnittpunkte der einzelnen Funktionsgraphen und machen Sie qualitative Ausgen über Extrempunkte und Steigungsverhalten von G(f) und - wenn möglich - auch über Wendepunkte und Grümmungsverhalten von G(f).
Aufgabe ist doch ein bisschen koplexer =)
wäre nett wenn mir jemand für b z.b. ein modell vorrechnet was ich dann auf die anderen anwenden kann.
Vielen Dank
Baggy |
    
Jasmin (häslein)

Mitglied
Benutzername: häslein
Nummer des Beitrags: 28
Registriert: 02-2003
| | Veröffentlicht am Mittwoch, den 02. April, 2003 - 20:26: | 
|
Willst du denn nun ein komplettes Aufgabenbeispiel oder nur den Definitionsbereich? |
    
mythos2002 (mythos2002)

Erfahrenes Mitglied
Benutzername: mythos2002
Nummer des Beitrags: 443
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 02. April, 2003 - 22:23: | 
|
Hi,
wenn du dir zunächst ein Bild (mittels "schneller" Diskussion, Nullstellen, Polstellen, Wertepaare ..) von der Funktion machst, weisst du dann nachher besser, wovon du redest.
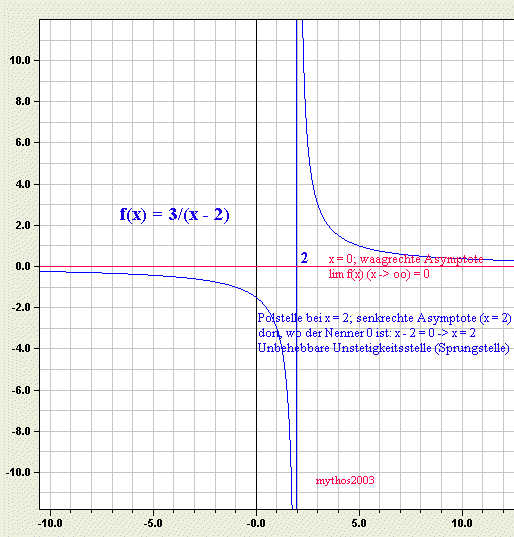
f(x) = 3/(x - 2)
Hier keine Nullstellen, denn f(x) = 0 ->
3/(x - 2) = 0
hat keine Lösung
Polstelle (Unstetigkeitsstelle): Nenner = 0
x - 2 = 0
x = 2
Diese Stelle ist aus der Definitionsmenge ausgeschlossen (die Funktion ist an dieser Stelle nicht definiert)
Bei x -> 2-0 (von links) geht f(x) gegen - oo
Bei x -> 2+0 (von rechts) geht f(x) gegen + oo
-> Vertikale Asymptote bei x = 2
Grenzwert:
lim f(x) (x -> oo) = lim [2/(x - 3)](x -> oo) = 0
Waagrechte Asymptote: x = 0
Asymptoten: Gerade, denen die Kurve beliebig nahe kommt, aber nicht schneidet (Berührung im Unendlichen).
Symmetrie (leicht ersichtlich): Zur x -Achse (horizontal) und zur Geraden y = 2 (vertikal)
Das Schaubild der Kurve ist eine gleichseitige Hyperbel (Asymptoten senkrecht aufeinander).
Extremwerte, Wendepunkte: (hier) keine
Krümmung:
Das Krümmungsverhalten ändert sich im Wendepunkt (wenn vorhanden) und hängt mit dem
Vorzeichen der 2. Ableitung zusammen: Ist dieses
positiv, ist die Krümmung dort auch positiv, auch als konvex bzw. links gekrümmt bezeichnet.
Ist die 2. Ableitung negativ, ist die Krümmung dort auch negativ, auch als konkav bzw. rechts gekrümmt bezeichnet.
Im Wendepunkt ist die Krümmung 0.
(-oo; 2): rechts gekrümmt (negativ), konkav
(2; +oo): links gekrümmt (positiv), konvex
Grafik:
<Asympt2.gif>
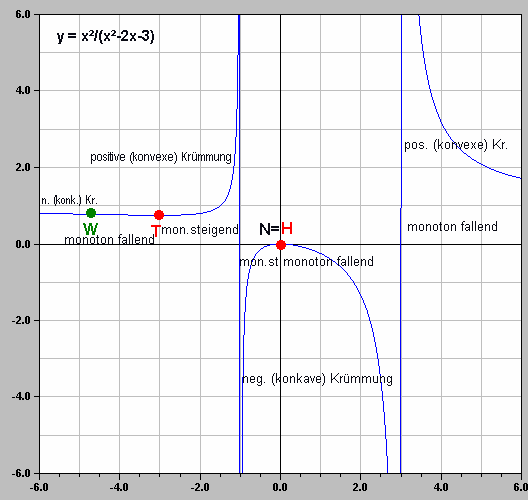
Zur Illustration anschließend noch ein anderes Beispiel!
Grafik
<Kurvendiskuss2.gif>
Gr
mYthos
|