| Autor |
Beitrag |
    
Claudia (Chroco83)

| | Veröffentlicht am Samstag, den 22. September, 2001 - 20:54: | 
|
Hey ihr lieben... ich habe tierische lücken in meinem mathevokabular-kurz gesagt ich habe null peilung!!!
wäre nett wenn ihr mir helfen könntet-wenn möglich mit erklärungen - will schließlich dabei lernen und mein abi schaffen :-)
also, hier die aufgabe:
für jedes t>0 ist eine funktion ft gegeben durch ft(x)= 1-e hoch(-tx). ihr schaubild von ft sei Kt.
a) untersuche Kt auf schnittpunkte mit der x-achse und asymptoten. zeichne K 1/2 (LE=2cm).
b) das schaubild Kt, die asymptote, die y-achse sowie die gerade mit der gleichung x=u (u>0) begrenzen eine fläche mit dem inhalt At(u). Berechne At(u)und lim At(u).
u-->+00
c) Pt(u/v) sei ein beliebiger punkt auf Kt im ersten feld. die parallelen zu den Koordinatenachsen durch Pt begrenzen mit der y-achse und der asymptote von Kt ein rechteck. Für welchen Wert von u wird der inhalt dieses Rechtecks maximal?
d) es sei g die gerade mit der gleichung x=1. die tangente in O(0/0) an Kt schneidet g in Pt, die normale in O(o/o) schneidet g in Qt. für welchen wert von t halbiert die x-achse die strecke PtQt?
bitte helft mir ... will nicht schon wieder 4 punkte bekommen ...:-((((
danke schonmal im vorraus!!!find ich echt klasse diese seite, sonst wäre ich ganz schön aufgeschmissen!
liebe grüße claudia |
    
N.

| | Veröffentlicht am Sonntag, den 23. September, 2001 - 17:14: | 
|
Hallo Claudia,
schau dir mal das Bild an, vieleicht kannst du danach ein paar Aufgaben selbst lösen....
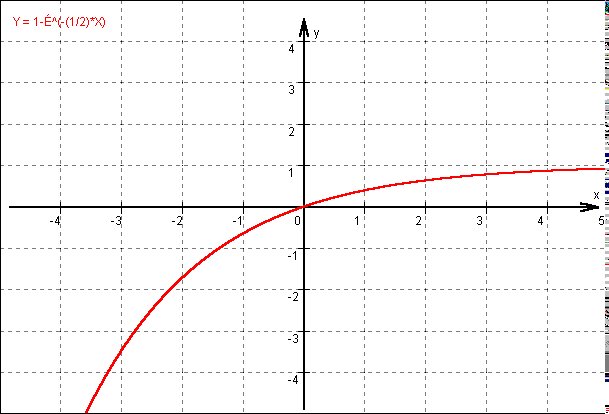
Gruß N. |
    
N.

| | Veröffentlicht am Sonntag, den 23. September, 2001 - 17:36: | 
|
Hallo Claudia,
hier ein paar Anmerkungen zum Bild:
1) Nullstellen:
Offensichtlich ist x=0 Nullstelle.
Beweis:
f(x)=1-e^(-(1/2)*x)
f(0)=0=1-e^(-(1/2)*x)
=>
e^(-(1/2)*x)=1...|ln
-(1/2)x=0
x=0
q.e.d
2) offensichtlich ist die Grade y=1 Asymtote der E-Funktion.
Beweis:
Grenzwertbetrachtung:
f(x)->¥
f(x)=1-e^(-(1/2)*x)
f(¥)=1-e^(-(1/2)*¥)=1
Der Term e^(-(1/2)*x) strebt für x->¥ gegen Null daher bleibt im Grenzfall nur die Eins übrig.
Ich hoffe das hilft weiter...
Gruß N. |
    
N.

| | Veröffentlicht am Sonntag, den 23. September, 2001 - 19:29: | 
|
Hallo Claudia,
noch ein paar Anmerkungen:
Meine Anmerkungen im letzten Beitrag gelten für alle Funktionen der Form
ft=1-e^(-tx)
für alle Funktionen dieser Funktionsschar ist die Nullstelle Null und die Asymptote die Gerade y=1 .
nun zur Teilaufgabe b)
Fläche zwischen g(x)=1 und ft(x)=1-e^(-tx)
A=òa b1-(1-e^(-tx))dx
A=òa be^(-tx)dx
A=ò0 ¥e^(-tx)dx
A[-(1/t)*e^(-tx)] Obere Grenze ¥;untere Grenze 0;
A=-(1/t)*e^(-t¥)-(-(1/t)*e^(-t*0))
A=0-(-(1/t))=1/t
Korrigiert mich falsch ich falsch liegen sollte....
Gruß N. |
    
N.

| | Veröffentlicht am Sonntag, den 23. September, 2001 - 20:46: | 
|
Hi Claudia,
nur noch ein paar Hinweise zur Nomenklatur:
Statt A wäre es konsequenter At für die Fläche zu setzen um zu zeigen, das die Fläche A vom Parameter t abhängt.
Statt e^(-t*¥) zu verwenden wäre es besser
lim e^(-t*x)
x->¥
Da ¥ keine Zahl ist mit der man rechnen kann, sollte man auch nicht so tun als ob ¥ so eine Zahl wäre.
Gruß N. |
|