| Autor |
Beitrag |
    
Jodokus

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 26. Mai, 2002 - 16:37: | 
|
Hallo.
Auf Seite http://www.zahlreich.de/cgi-bin/hausaufgaben/show.cgi?tpc=4244&post=102474#POST102474 wurde bewiesen, dass
Sk=1oo k/2k = 2 ist.
wie beweist man, dass
Sk=1oo k²/2k = 6
Sk=1oo k³/2k = 26
Sk=1oo k4/2k = 150
etc.
Falls es hilft:
für s(n) = Sk=1oo kn/2k
scheint eine rekursive Formel zu gelten:
s(n) = 1 + Sm=0n-1 (n über m) * s(m)
wobei s(0) = Sk=1oo k0/2k = 1 ist.
|
    
Xell (vredolf)

Fortgeschrittenes Mitglied
Benutzername: vredolf
Nummer des Beitrags: 66
Registriert: 03-2002
| | Veröffentlicht am Sonntag, den 26. Mai, 2002 - 22:23: | 
|
Hallo Jodokus!
Ich schlage eine Schritt-für-Schritt-Zerlegung der Summe
vor, wie sie uns auch schon bei den mittlerweile zwei
vorherigen Aufgaben zum Ziel geführt hat.
Reihen der Form sum(k^n/q^k,k=1..inf) lassen sich demnach
stets auf Summen der entsprechenden geometrischen Reihe
sum(1/q^k,k=1..inf) zurückführen. Es gilt also sicher:
sum(k^n/q^k,k=1..inf) = sum(a_j * sum(1/q^k,k=j..inf),j=1..inf).
Hierbei stellen die a_j die zu bestimmenden Koeffizienten
dar.
Weiter können wir uns stets zunutze machen, dass
sum(1/q^k,k=j..inf) = 1/q * sum(1/q^k,k=j-1..inf) gilt
für j>0.
Gruß und gute N8,
X. |
    
Xell (vredolf)

Fortgeschrittenes Mitglied
Benutzername: vredolf
Nummer des Beitrags: 67
Registriert: 03-2002
| | Veröffentlicht am Montag, den 27. Mai, 2002 - 16:02: | 
|
Hi Jodokus!
Kleine Aktualisierung:
R(n) := sum(k^n/q^k,k=1..inf)
Bereits berechnet habe ich
R(0) = q/(q-1)
R(1) = q/(q-1)^2
R(2) = (q^2+q)/(q-1)^3
Damit ergibt sich der Spezialfall von R(2) mit q=2 zu
R(2) = (4+2)/1^3 = 6.
Unsere bisher bewiesenen Reihen fügen sich nahtlos ein:
R(1) mit q=2: R(1) = 2/1^2 = 2
Ebenso R(2) mit q=3:
R(2) = (9+3)/2^3 = 12/8 = 3/2
Die explizte Darstellung von R(n) herzuleiten würde das
Thema angemessen abrunden.
Gruß,
X. |
    
Mathenixpeiler

Unregistrierter Gast
| | Veröffentlicht am Montag, den 27. Mai, 2002 - 16:09: | 
|
Ah ja,alles klar,total verständlich,so hätte ich das auch gemacht...das ist Mathe oder bin ich da komplett falsch? |
    
Jodokus

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 31. Mai, 2002 - 21:11: | 
|
Hi Xell, danke auch hier für das Zeigen dieses Weges.
Ich habe für n=2..4 bisher folgende Formeln erhalten:
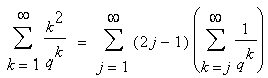
R(2) = Sum( (2*j-1) * Sum(1/q^k,k=j..infinity) , j=1..infinity)
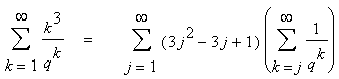
R(3) = Sum( (3*j^2 - 3*j + 1) * Sum(1/q^k,k=j..infinity) , j=1..infinity)
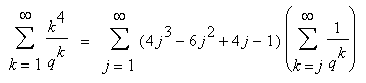
R(4) = Sum( (4*j^3 - 6*j^2 + 4*j - 1) * Sum(1/q^k,k=j..infinity) , j=1..infinity)
so dass sich die allgemeine Formel (leider in einer zu wenig expliziten Form) schon erahnen lässt:
R(n) = Sum( (j^n - (j-1)^n) * Sum(1/q^k,k=j..infinity) , j=1..infinity)
aber ich habe keine Idee, wie ich von hier aus auf deine Darstellung
R(2) = (q^2+q)/(q-1)^3 kommen kann.
Gruß,
Jodokus |
    
Xell (vredolf)

Fortgeschrittenes Mitglied
Benutzername: vredolf
Nummer des Beitrags: 74
Registriert: 03-2002
| | Veröffentlicht am Samstag, den 01. Juni, 2002 - 01:35: | 
|
Hallo Jodokus!
Den Zusammenhang mit R(n) = (j^n - (j-1)^n)* ... hab ich
mir auch schon klargemacht. Um meine Vermutung zur Darstellung
von R(n) zu verfolgen, setze ich dich nun über Ergebnisse
in Kenntnis, die ich mittels eines CAS erhalten habe.
Nun eine Liste mit Faktorisierungen von R(n), n=0..10
R(0) = 1/(q-1)
R(1) = q/(q-1)^2
R(2) = q * (q+1)/(q-1)^3
R(3) = q * (q^2 + 4q + 1)/(q-1)^4
R(4) = q * (q^3 + 11q^2 + 11q + 1)/(q-1)^5
R(5) = q * (q^4 + 26q^3 + 66q^2 + 26q + 1)/(q-1)^6
R(6) = q * (q^5 + 57q^4 + 302q^3 + 302q^2 + 57q + 1)/(q-1)^7
Demnach dürfte die Form von R(n) klar sein:
R(n) = q * (q^(n-1) + a_{n-2} * q^(n-2) + ... + a_1 * q + 1)/(q-1)^(n+1)
Bleibt noch, das Prinzip, nach dem die a_i zu berechnen sind,
herauszufinden.
Hier bediene ich mich einer Intenet-Datenbank, die zahlreiche
Folgen aufführt (http://www.research.att.com/~njas/sequences/).
Ergebnis:
a_1 = 2^n - n - 1 (sog. "Eulersche Zahlen")
Da das Polynom offenbar symmetrisch ist, ist damit auch
a_{n-2} = a_1
Anscheinend lassen sich sämtliche Koeffizienten durch das
Eulersche Dreieck (?) bestimmen. Das Problem dürfte damit
gelöst sein. Die Beschäftigung mit besagtem Dreieck er-
scheint mir optional.
Hier ein Link für Hinweise: http://www.research.att.com/cgi-bin/access.cgi/as/njas/sequences/eisA.cgi?Anum=008292
Soviel erstmal von mir heute Abend,
Xell |
|