| Autor |
Beitrag |
    
TitanZwick

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 02. Mai, 2002 - 21:34: | 
|
Hallo,
Wer kann mir Schritt für Schritt bei der
Lösung der folgenden Aufgabe über zwei
bestimmte Integrale helfen ?
U ist das Integral von x = 0 bis x =1 über
f(x) = 1 /sqrt(1 - x^3),
V ist das Integral von t = 0 bis t = Pi/2 über
g(t) = (sint * cos t ) ^ 1/3
Man beweise, dass
U*V = 1/6*Pi *2^(2/3)*3^(1/2) gilt.
MfG
Titan(Zwick)
|
    
orion (orion)

Erfahrenes Mitglied
Benutzername: orion
Nummer des Beitrags: 192
Registriert: 11-2001
| | Veröffentlicht am Freitag, den 03. Mai, 2002 - 09:46: | 
|
Hallo :
Beide Integrals lassen sich auf das Beta-Integral
B(x,y) := int[0...1]t^(x-1)*(1-t)^(y-1) dt
= Gamma(x)*Gamma(y)/Gamma(x+y); x,y > 0
zurückführen.
1) Substituiere in U :
x = u^(1/3) ==> dx = (1/3)*u^(-1/3). Dann wird
U = (1/3)*int[0...1]u^(-2/3)*(1-u)^(-1/2) du
= (1/3)*B(1/3 , 1/2).
2) Für V wähle die Substitution
sin(t) = z^(1/2) ==> cos(t) = (1-z)^(1/2),
dt = (1/2)*z^(-1/2)*(1-z)^(-1/2) ==>
V = (1/2)*int[0...1]z^(-2/3)*(1-z)^(-2/3) dz
= (1/2)*B(1/3,1/3).
mfg
Orion
|
    
H.R.Moser.megamath

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 03. Mai, 2002 - 10:25: | 
|
Hi Titan,
Eine wahrhaft titanische Aufgabe, die Du da stellst !
Wo sollen wir beginnen ?
Der Kenner spürt, dass beide Integrale mit Hilfe der
Begriffe aus der Theorie (und Praxis) der
Beta- und Gammafunktion ermittelt werden können.
Die notwendigen Vorkenntnisse habe ich kürzlich
bei der Lösung eines mit Deinen Integralen nahe
verwandten Integrals zusammengestellt.
Diese Zusammenstellung der Grundformeln folgt
hier in extenso:
1.
Das so genannte Eulersche Integral erster Gattung,
die Betafunktion B(p,q), ist das Integral
B(p,q) = int [x^(p-1) * (1-x)^(q-1)*dx ] , (p>0,q>0)……(1.1)
untere Grenze 0 , obere Grenze 1.
Mit Hilfe der Gammafunktion G(p) =GAMMA(p)
( Eulersches Integral zweiter Gattung)
G(p) = int [e ^ (-x) * x^(p-1) * dx ] ,(p>0) ,
untere Grenze 0 ,obere Grenze unendlich,
kann B(p,q) auch so geschrieben werden:
B(p,q) = [G(p) * G(q) ] / [G( p + q ) ] ............................(1.2)
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
2.
Für G(x) gilt für x>0 die Funktionalgleichung
G(x +1)= x* G(x) .................................................... ......(2.1)
Also für p >1
G(p)=(p-1) * G(p-1)……………………………………(2.2)
3.
Die Gammafunktion genügt einer weitern
Funktionsgleichung:
G(x) G(1-x) = Pi / sin(Pi *x), (x nicht ganzzahlig)........(3.1)
Mit (2.2) wird daraus:
G(1-p)*G(1+p) = p*Pi/sin(p*Pi)………………………(3.2)
Für x = ½ kommt sofort (!) :
G(½) = wurzel(Pi)..........................................................(3.3)
4.
Mit xk = G(k/12) erhalten wir :
x3 * x4 = Pi* wurzel(2)..................................................(4.1)
d.h.
G(¾) = Pi* wurzel(2) / G(¼)..........................................(4.2)
5.
Reduktion auf Argumente zwischen null und eins
mit Hilfe der Formel (3.2.)
G(5/4) = Pi * wurzel(2) / {4*G(¾ )}..............................(5.1.)
G(7/4) = 3 Pi * wurzel(2) / {4*G(¼)}............................(5.2.)
Nun sind alle nötigen Vorbereitungen getroffen,
und es geht jetzt darum, die vorgelegten Integrale
anzusteuern.
Es ist hilfreich,, im Integral der Formel 1.1 die
folgende Substitution auszuführen :
x = (sin t)^2 , 1 - x = ( cos t )^2 , dx = 2 sin t cos t
Für B(p,q) kann nach(1.1) geschrieben werden
(untere Grenze 0 , obere Grenze ½ Pi ) :
B(p,q ) = 2 int [ (sin t)^(2p-1)*(cos t)^(2q –1)* dt ]…..(6)
= [G(p)*G(q) ] / [G(p+q) ]
Jetzt trennen sich die Wege für die Berechnung der
Integrale U und V.
A]
Wir berechnen als Ausgangspunkt zur Berechnung
von U zunächst das Integral
J = int [(sin t)^(-1/3) * dt ]
mit der unteren Grenze 0 und der oberen Grenze 1
Zusätzlich benötigen wir die Beziehung
x4*x8 =G(1/3)*G(2/3) = G(4/12)*G(8/12) =
Pi/sin(4 Pi / 12) = 2 * 3 ^ (- ½) * Pi………………… (7)
Wir setzen jetzt in (6) p = q = 1/3 ein; wir
erhalten damit 2p – 1 = 2 q – 1 = - 1/3
und die Integralformel:
(untere Grenze 0,obere Grenze ½ Pi)
B = 2 * int [dt /{ (sin t * cos t)^(1/3) }] =
[G(1/3)] ^ 2 / [G(2/3)] ; mit (7) kommt:
B = wurzel(3)* [G(1/3)] ^ 3 / (2*Pi),
also
int [dt /{ (sin t * cos t)^(1/3) }] =
= wurzel(3)* [G(1/3)]^3 / (4*Pi)........................... ..(8)
untere Grenze 0,obere Grenze 1
Nun substituieren) wir in (8):
2 t = u , also 2 * sin t cos t = sin(2t) = sin u
und dt = ½ du.
Es entsteht mit den Grenzen u = 0 bis u = Pi
int [ du / (sin u )^1/3 ] =
= wurzel(3)* [G(1/3)]^3 / [2*Pi*2^(1/3)]
Dieses Integral stellt, wie man leicht bestätigt,
gerade 2 * J dar, somit gilt:
J = int [(sin t ) ^ (-1/3) * dt] =
= wurzel(3)* [G(1/3)]^3 / [4*Pi*2^(1/3)]................(9)
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Um auf Dein Integral U zu stossen,
substituieren wir folgendermassen :
(sin t) ^2 = u^3 , also (cos t)^2 = 1 - u ^ 3
sin t = u ^(3/2), also (sin t) ^ (1/3) = wurzel(u),
weiter:
cos t * dt = 3/2* wurzel(u) * du,
daraus folgt zwanglos:
dt = 3 * wurzel(u)*du / [2*wurzel(1-u ^3 )]
Durchführung dieser Substitution im Integral (9)
Neue Grenzen: u = 0 bis u = 1 an Stelle von
t = 0 bis t = ½ Pi ; es kommt neu:
J = int [(sin t)^(-1/3) * dt ] = 3/2* int[du / wurzel(1-u^3)]
= wurzel(3)* [G(1/3)]^3 / [4*Pi*2^(1/3)]
Wegen J = 3/2 *U folgt daraus als ein
erstes Teilresultat.
U = int[du / wurzel(1-u^3)] =
[G(1/3)] ^ 3 / [2*Pi 2^(1/3)wurzel(3)] ~ 1.402182105
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
B]
Nun soll der Wert des Integrals V bestimmt werden !
Für p = q = 2/3 wird aus Gleichung (6)
B(2/3;2/3) = 2 * int [(sin t)^(1/3) * (cos(t)^1/3 * dt ] =
[G(2/3)]^2 /G(4/3)= 3*[G(2/3)]^2/G(1/3) =
3*[G(2/3)]^3 / [G(1/3)*G(2/3)] oder wegen Gl.(7)
und wegen B = 2 V entsteht das zweite Teilresultat
V = int [(sin t * cos t ) ^1/3 dt ] =
= {3 * wurzel(3) / (4*Pi) } * G(2/3)^3 ~1.026695109
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
C]
Es ist nun ein Kinderspiel, P = U*V zu berechnen ,
wenn man wiederum Formel (7), d.h. die Relation
G(1/3)*G(2/3) = 2 * 3 ^ (- ½) * Pi benützt.
Resultat.
P = 1/6 * Pi* 2^2/3 *wurzel(3)
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
wie behauptet wurde.
Ein passendes Zitat zum Abschluss:
Tanta molis erat Romanam condere gentem
(Vergil,Aeneis 1,33)
So grosser Mühsal bedurfte es, das Volk der Römer
zu begründen.
Mit freundlichen Grüßen
H.R.Moser,megamath.
.
|
    
Friedrich Laher (friedrichlaher)

Erfahrenes Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 250
Registriert: 02-2002
| | Veröffentlicht am Freitag, den 03. Mai, 2002 - 12:29: | 
|
HALLO H.R.moser.megamath
will das Forum nicht mit möglicherweise Falschem belasten. Siehst Du bitte, mal
hier
nach.
(Link BEGRENZTE ZEIT GÜLTIG, dann wieder anderer Inhalt)
|
    
N.

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 03. Mai, 2002 - 13:25: | 
|
Ich verstehe deine Zurückhaltung mit dem Ling nicht.
Wenn sie falsch ist kann Herr Moser den Fehler hier öffentlich ausbügeln; dazu ist möglicherweise die Überarbeitung der gesammten Rechnung notwendig-wäre schön, wenn man sie hier dann zeitunabhängig griffbereit hätte.
Ist sie richtig würden sich noch andere Menschen über eine alternative Rechnung Marke "Holzhammer"
freuen.
in Beiden Fällen wäre es also sinnvoll die Rechnung zu haben-
Also Herr Megamath-Stimmt die folgende Rechnung soweit?
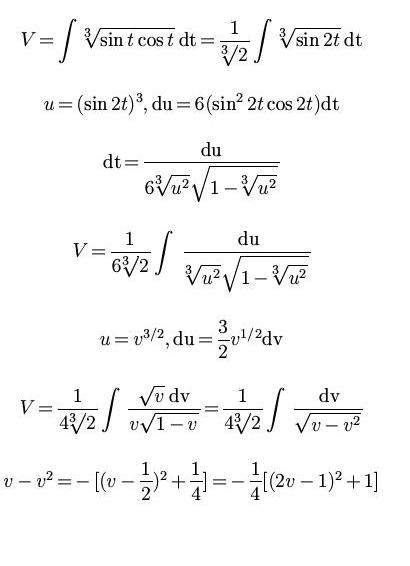
Gruß N. |
    
orion (orion)

Erfahrenes Mitglied
Benutzername: orion
Nummer des Beitrags: 193
Registriert: 11-2001
| | Veröffentlicht am Freitag, den 03. Mai, 2002 - 15:53: | 
|
Korrektur zu meinem Beitrag Nr.192:
F.Laher macht mich dankenswerterweise auf einen Rechenfehler in den Exponenten aufmerksam.
Tatsächlich habe ich V falsch abgeschrieben und mit dem Exponenten - 1/3 statt 1/3 im
Integral gerechnet. So komme ich nun auf demselben
Weg zu dem (hoffentlich) korrekten Zwischenresultat.
V = (1/2)*B(2/3,2/3)
Das ergibt
UV =(1/6)*G(1/2)G(1/3)(G(2/3))^2/G(5/6)G(4/3).
Mit Hilfe von G(1/2) = sqrt(pi) sowie
G(x+1)=x*G(x),
G(x)G(1-x) = pi/sin(pi*x),
G(2x) = (2*pi)^(-1/2)*2^(2x-1)*G(x)*G(x+1/2)
kommt man zum behaupteten Resultat.
Orion
|
    
H.R.Moser,megamath

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 03. Mai, 2002 - 20:31: | 
|
Hi Friedrich, Hi Niels ,
Expertise ohne Gewähr und ohne Haftung:
Die Sache sieht zunächst vielversprechend aus.
Ein Rechenfehler ist auf den ersten Blick
nicht ersichtlich.
Die gewählte erste Substitution u = (sin 2 t ) ^3
ist jedoch nicht zulässig, da sie die Bedingung
der Eineindeutigkeit der Substitutionsfunktion
u = u(t) nicht erfüllt.
Es muss sowohl u = Phi(t) als auch t = Psi(u)
eindeutig sein.
Empfehlung: Skizziere die Funktion u = (sin 2 t )^3
über dem Interval 0 <= t <= ½*Pi
Stichworte : Gültigkeitsbereiche, Umkehrbarkeit
der gewählten Substitution.
In einem mir vorliegenden amerikanischen
Standardwerk zur Integration wird dazu vermerkt:
„Be sure that the function substituted is ONE-TO-ONE
and continuous …”.
Das wärs !
MfG
H.R.Moser,megamath
|
    
H.R.Moser,megamath

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 03. Mai, 2002 - 21:03: | 
|
Hi Titan,
Nachdem Orion und ich Dir gezeigt haben,
wie man es macht,
möchte ich Dir eine kleine Uebungsaufgabe
unterbreiten:
Sei f(t) = (sin t *cos t) ^(1/3) , g(t) = 1 / f(t)
A und B sind die Integrale über f(t) bezw. g(t)
je in den Grenzen t = 0 bis t = ½* Pi.
Man beweise die coole Relation:
A * B = ½ * Pi * sqrt(3)
°°°°°°°°°°°°°°°°°°°°°°°°
Viel Spass !
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Friedrich Laher (friedrichlaher)

Erfahrenes Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 254
Registriert: 02-2002
| | Veröffentlicht am Freitag, den 03. Mai, 2002 - 21:44: | 
|
@Moser: und wenn man das Integrationsintervall aufteilt?
Oder eben nur ein Intervall gefordert
ist, in dem die Subst. eindeutig ist?
(Beitrag nachträglich am 03., Mai. 2002 von friedrichlaher editiert) |
    
Friedrich Laher (friedrichlaher)

Erfahrenes Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 255
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 04. Mai, 2002 - 10:50: | 
|
@Moser: und ist denn dann die Subst. sin t = z^(1/2) überhaupt zulässig? ( wie weiter oben orion vorschlägt )
(Beitrag nachträglich am 04., Mai. 2002 von friedrichlaher editiert) |
    
H.R.Moser,megamath

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 04. Mai, 2002 - 11:29: | 
|
Hi Friedrich,
Die Vorbehalte, die ich gegen Deine Methode
angemeldet habe, muss ich aufrecht erhalten.
Dazu einige Bemerkungen.
1)
An und für sich darf ein Integrationsintervall
aufgeteilt werden und es dürfen Symmetrien
ausgenützt werden.
Aber die gewählte erste Substitution ist
gleichwohl fragwürdig.
2)
Bei der Umformung des Ausdrucks v – v^2
in Deiner Arbeit steckt ein Fehler:
v – v^2 stimmt nicht mit dem angegebenen
Term überein
3)
Für das unbestimmte Integral
F = int [dv / sqrt(v-v^2)] erhalten wir
F = arc sin (2 v – 1) + C
4)
Nachdrücklich schlage ich Dir vor:
Ziehe die Rechnung mit Deiner Methode voll durch
und ermittle dadurch einen Näherungswert für das
gegebene bestimmte Integral V.
Mit der von mir durchgeführten Methode, welche
das zweifellos richtige Resultat für V ergibt , nämlich
V = 3 * sqrt(3) / (4*Pi) * [GAMMA(2/3)] ^ 3
liefert den Näherungswert.
V ~ 1,026695109 (Nachprüfung mit Maple !)
°°°°°°°°°°°°°°°°°°
5)
Ich bin der Meinung, dass zur Ermittlung eines
Integrals der vorliegenden Art stets adäquate
Mittel eingesetzt werden sollten, also im
aktuellen Fall sind das eindeutig die
Beta- oder Gammafunktion, deren Einsatz
in der Tat zum Erfolg führte; voilà !
Auf anscheinend elegantere elementare Methoden
sollte tunlichst verzichtet werden.
6)
Auf die Problematik bei der Anwendung der
Substitutionsmethode werde ich bei Gelegenheit
anhand eines andern Beispiels näher eingehen.
7)
die Substitution sin t = z ^ ½ ist zulässig,
sofern sin t > = 0 gilt ;ich komme auf diese Frage zurück
bei der Bearbeitung des unter Punkt 6) erwähnten Beispiels.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
H.R.Moser,mgamath

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 04. Mai, 2002 - 15:17: | 
|
Hi Friedrich,
Die Vorbehalte, die ich gegen Deine Methode
angemeldet habe, muss ich aufrecht erhalten.
Dazu einige Bemerkungen.
1)
An und für sich darf ein Integrationsintervall
aufgeteilt werden und es dürfen Symmetrien
ausgenützt werden.
Aber die gewählte erste Substitution ist
gleichwohl fragwürdig.
2)
Bei der Umformung des Ausdrucks v – v^2
in Deiner Arbeit steckt ein Fehler:
v – v^2 stimmt nicht mit dem angegebenen
Term überein
3)
Für das unbestimmte Integral
F = int [dv / sqrt(v-v^2)] erhalten wir
F = arc sin (2 v – 1) + C
4)
Nachdrücklich schlage ich Dir vor:
Ziehe die Rechnung mit Deiner Methode voll durch
und ermittle dadurch einen Näherungswert für das
gegebene bestimmte Integral V.
Mit der von mir durchgeführten Methode, welche
das zweifellos richtige Resultat für V ergibt , nämlich
V = 3 * sqrt(3) / (4*Pi) * [GAMMA(2/3)] ^ 3
liefert den Näherungswert.
V ~ 1,026695109 (Nachprüfung mit Maple !)
°°°°°°°°°°°°°°°°°°
5)
Ich bin der Meinung, dass zur Ermittlung eines
Integrals der vorliegenden Art stets adäquate
Mittel eingesetzt werden sollten, also im
aktuellen Fall sind das eindeutig die
Beta- oder Gammafunktion, deren Einsatz
in der Tat zum Erfolg führte; voilà !
Auf anscheinend elegantere elementare Methoden
sollte tunlichst verzichtet werden.
6)
Auf die Problematik bei der Anwendung der
Substitutionsmethode werde ich bei Gelegenheit
anhand eines andern Beispiels näher eingehen.
7)
die Substitution sin t = z ^ ½ ist zulässig,
sofern sin t > = 0 gilt ;ich komme auf diese Frage zurück
bei der Bearbeitung des unter Punkt 6) erwähnten Beispiels.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
H.R.Moser,megamath

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 04. Mai, 2002 - 15:20: | 
|
Hi Friedrich,
Hier das angekündigte Beispiel. zur
Substitutionsmethode
Ich entnehme es dem bereits erwähnten
amerikanischen Standardwerk zur Integration.
von Robert C.Weast.
abs(u) bedeutet: „Absolutbetrag von u“
Das Zitat erfolgt in der Originalsprache ,
um Uebersetzungsfehler zu vermeiden.
Example:
int [ x ^ 4 / sqrt (a^2 - x^2) * dx ]
Here we make the substitution x = abs(a)* sin t.
Then dx = abs(a) * cos t * dt , and
sqrt (a^2 - x^2) = sqrt [ a^2 - a^2* {sin t}^2 ]
= abs(a) * sqrt [1 – {sin t }^ 2 ] =
abs [a * cos t].
Notice the absolute value signs. It is very important
to keep in mind that a square root radical always
denotes the positive square root , and to assure the sign
is always kept positive.
Thus sqrt(x^2) = abs(x).
Failure to observe this is a common cause of errors
in integration.
Notice also that the indicated substitution is not a
one–to-one function, that is , it does not have a unique
inverse.Thus we must restrict the range of t in such a
way as to make the function one–to -one.
Fortunately,this is easily done by solving for t
t = arc sin [x / abs(a) ]
and restricting the inverse sine the to the principal
values,
- ½ Pi < = t <= ½ Pi
Thus the integral becomes
int [{ a^4 (sin t)^4 abs(a) * cos t }/{abs(a)*abs(cos t)} *dt]
Now, however, in the range of values chosen for t ,
cos t is always positive.Thus we may remove the absolute
value signs from cos t in the denominator.(This is one
of the reasons that the principal values of the inverse
trigonometric functions are defined as they are.)
Then the cos t terms cancel,and the integral becomes
a ^ 4 * int [ (sin t) ^ 4 * dt ]b
By application of integral formulas 299 and 296,
we integrate this to
- a^4 * ¼ (sin t)^3*cos t –3/8*a^4*cos t * sin t +3/8*a^4 * t + C
We now must perform the inverse substitution to get
the result in terrms of x. We have
t = arc sin [ x / abs(a) ]
sin t = x / abs (a)
Then
cos t = (+ -) sqrt [1-(sin t)^2)] =
(+-)sqrt[1-x^2/a^2] = (+-)sqrt[a^2 – x^2 ] / abs (a)
Because of the previously mentioned fact that cos t
is positive,we may omit the (+-)sign.
The reverse substitution then produces the final answer
int [ x ^ 4 / sqrt (a^2 - x^2) * dx ] =
- ¼ x^3*sqrt(a^2-x^2) –3/8a^2*x *sqrt(a^2-x^2) +
+ 3/8*a^4*arc sin [x/abs(a)] + C
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Ende Zitat
So subtil sollte man bei der Substitution in der
Integralrechnung vorgehen !
Mit freundlichen Grüßen
H.R.Moser,megamath.
|
    
TitanZwick

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 05. Mai, 2002 - 14:40: | 
|
Hallo H.R.Moser,megamath,
Hallo Orion
Besten Dank für eure Hilfen
MfG
Titan Zwick
|
    
Friedrich Laher (friedrichlaher)

Erfahrenes Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 260
Registriert: 02-2002
| | Veröffentlicht am Sonntag, den 05. Mai, 2002 - 14:57: | 
|
Dank H.R.Moser,
für
Geduld und Mühe.
"Meine Methode", ausgehend von arcsin hab ich, hoffentlich ohne weitere Rechenfehler, durchgezogen und sehe ein daß das veblüffend einfache Ergebnis ( ??? Unbest.Int = (8t - Pi)/(8*21/3) ???) nicht stimmen kann.
Im
link hatte ich allerdings nicht nur die Herleitung angegeben, sondern auch hoffentlich klar gemacht,
daß ich kein Uni/Hochschulausbildung habe,
das
Problem also garnicht anders angehen konnte.
mfG
F.
mein Briefkasten steht offen.
|
    
H.R.Moser,megamath

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 05. Mai, 2002 - 16:58: | 
|
Hi Friedrich,
Obwohl Du das Ziel mit Deiner Methode nicht
ganz erreicht hast, verdienst Du für
Deinen Einsatz und Deine Beharrlichkeit
Dank und Anerkennung !
Mit besten Grüssen
H.R.Moser,megamath
|
|