| Autor |
Beitrag |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Dienstag, den 12. Februar, 2002 - 19:44: | 
|
Hallo!
Ich suche eine Lösung folgender Aufgabe (vielleicht habt ihr mehr Ahnung):
Man zeige folgende Identitäten:
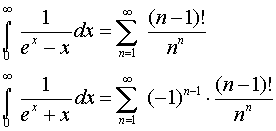
Schön, nicht wahr? Aber wie um alles in der Welt kommt man darauf? Reihenentwicklung?
Sollte irgend jemand einen vielversprechenden Ansatz haben, bitte unbedingt posten!!
Kay S. |
    
H.R.Moser,megamath

| | Veröffentlicht am Mittwoch, den 13. Februar, 2002 - 19:12: | 
|
Hi Kai,
Vorankündigung:
Ich werde auf Deine sehr schöne, aber etwas anspruchsvolle Aufgabe
so bald wie möglich eingehen
Ich habe zuvor noch dringende Arbeiten in Haus und Hof zu verrichten !
Bis dann
H.R.Moser,megamath |
    
H.R.Moser,megamath

| | Veröffentlicht am Mittwoch, den 13. Februar, 2002 - 20:12: | 
|
Hi Kai
Es ist bereits Tradition geworden, dass ich Deine Fragen mit Gegenfragen
kontere und zwar in Form von Integralen, welche sich bezüglich
Aesthetik und Schwierigkeitsgrad ebenfalls sehen lassen dürfen.
Die beiden Integrale mit Resultaten (ohne Beweise) , die Du in Deine
Sammlung aufnehmen kannst, lauten:
1.
int [ sinh (ax) / (e^x +1) * dx ] = ½ * Pi / sin (a*Pi) - 1 / (2*a)
untere Grenze 0 , obere Grenze unendlich.
2.
int [ sinh (ax) / (e^x - 1) * dx ] = 1 / (2*a) - ½ * Pi * cot (a*Pi)
untere Grenze 0 , obere Grenze unendlich.
Aber nun zu Deiner Aufgabe
Für beide empfehle ich Dir das folgende Integral (H) zu benützen ,dessen
Herleitung nicht allzu schwierig ist ; ich kann diese getrost Dir überlassen
Es gilt:
int [ e ^(- n * x) * x ^ (n -1) * dx ] = (n – 1) ! / n^n..... ..( H )
untere Grenze 0 , obere Grenze unendlich.
Rechts steht nun ein Term in n , über den in Deiner Aufgabe summiert wird,
entweder alle Summanden tel quel, oder mit alternierenden Vorzeichen.
Bildest Du auch links die entsprechenden Summen (n = 1 ad infinitum) der
Teilintegrale aus (H) , so erkennst Du im Integranden des zusammengefassten Integrals
eine unendliche geometrische Reihe:
Anfangsglied a = e ^ -x , Quotient q = e ^ -x * x , Summe s = a / ( 1 – q )
= 1 / ( e ^ x – x) und dies ist gerade der Integrand im Integral bei Deiner
ersten Aufgabe.
Bei der zweiten Aufgabe ist der Quotient der geometrischen Reihe
q = - e^-x * x ,
die Summe daher 1 / ( e ^ x +x).
Hoffentlich habe ich behilflich sein können !
Mit freundlichen Grüßen
H.R.Moser. |
    
H.R.Moser,megamath

| | Veröffentlicht am Donnerstag, den 14. Februar, 2002 - 12:59: | 
|
Hi Kay,
Bevor alle unsere Arbeiten wegen des defekten Achivs
im Orkus verschwinden, noch ein zusätzlicher Beitrag
meinerseits zum Thema.
Es folgen ein paar weitere Beispiele interessanter Integrale
mit unterer Grenze null, oberer Grenze unendlich,
darunter ein paar prominente.
Die meisten von ihnen enthalten einen Parameter a.
Du kannst sie in Deine Sammlung aufnehmen
Einige wenige davon werde ich im Anhang herleiten.
1.
J1 = int [(1- e^(- a * x)) * sin x / x * dx ] ,
untere Grenze 0, obere Grenze unendlich.
Es gilt:
J1 = arc tan a
2
J2 =int [sin x / x ] * dx
untere Grenze 0, obere Grenze unendlich.
Es gilt:
J2 = ½ * Pi
3.
J3 = int [e^ ( - a * x ) * sin x / x * dx ] ,
untere Grenze 0, obere Grenze unendlich.
Es gilt:
J3 = arccot a
4.
J4 = int [ {e^(-x) – e ^(-a*x) }/ x * dx ]
untere Grenze 0, obere Grenze unendlich.
a > 0.
Es gilt:
J4 = ln a .
5.
J5 = int [ e^ (- a * x ) * x ^ (n -1) * dx ] ,
untere Grenze 0, obere Grenze unendlich.
n positiv ganz, a > 0
Es gilt:
J5 = (n-1)! / a ^ n
6.
J6 = int [ sin x * cos( a * x ) / x * dx ]
dieselben Grenzen.
Es gilt:
J6 =
· ½ Pi für abs ( a ) < 1
· ¼ Pi für abs ( a ) = 1
· 0 für die übrigen a-Werte.
7.
Als Gegenstück zum sinus diene ein sinus hyperbolicus:
J7 = int [x / sinh ( a * x ) * dx ] mit den genannten Grenzen.
Resultat:
J7 = (Pi)^2 / (4*a ^2)
8.
Oder mit cosinus hyperbolicus:
J8 = int [1 / cosh ( a * x ) * dx ],dieselben Grenzen.
Resultat:
J8 = Pi / 2 * a
Beachte: J7 = J8 ^ 2
u.s.w.
Anmerkungen
1) Herleitung von 1.
Aus der bekannten Formel (unbestimmtes Integral)
int [e^(-a x)*sin (b x)*dx ] = -a/(a^2 + b^2) * e^(-a x )* [sin(b x) +b/a*cos (b x )]
folgt für b=1 für das bestimmte Integral mit unterer Grenze null, oberer Grenze
unendlich :
J = int [e^(-a x ) * sin x * dx ] = 1 / (1 + a ^ 2 )
Nun integrieren wir nach a zwischen den Grenzen a = 0 und a
(auf der linken Seite Integration unter dem Integral!) ; es kommt:
J1 = int [(1- e ^ (- a * x)) * sin x / x * dx ] = arc tan a
untere Grenze 0, obere Grenze unendlich
w.z.z.w.
2) Herleitung von 2.
Lässt man im Integral J1 den Parameter a nach unendlich gehen, entsteht
unmittelbar J2 !
3) Herleitung von 3.
Es gilt offenbar:
J3 + J1 = J2, also
J3 = ½* Pi - arctan (a) = arcctg (a)
4) Herleitung von 4.
Wir leiten nach dem Parameter a ab und erhalten:
d(J) / da = int [e^(-a x)* dx ] = 1 / a
Nach wie vor ist 0 die untere Grenze des Integrals und unendlich die obere.
Somit durch Integration (Integrationskonstante C = 0):
J4 = int [ da /a ] = ln a.
5)
Dieses Integral kannst Du im Spezialfall a = n , wie ich in meinem letzten
Beitrag ausgeführt habe, zum Beweis Deiner Formeln benützen.
Der Spezialfall lautet in extenso :
J5* = int [ e^ (- n* x ) * x ^ (n -1) * dx ] = (n -1)! / n ^ n
untere Grenze 0, obere Grenze unendlich
Diese Formel lässt sich relativ einfach beweisen, z.B.
auch mit vollständiger Induktion (Schluss von n auf n+1).
Lassen wir das auf sich beruhen !
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Donnerstag, den 14. Februar, 2002 - 22:03: | 
|
Hi,
Es ist wirklich erstaunlich: da stellt man eine Aufgabe ins Board, an der man wochenlang grübelt und einen Tag später hat der Megamath die perfekte Lösung dazu! (Gratulation!)
Doch zur Sache: Die Aufsummierung über n ergibt tatsächlich eine geometrische Reihe, deren Summe direkt das Integral ergibt. Voraussetzung aber ist die erwähnte Formel
ò0 ¥ e-nx * xn-1 = (n-1)!/nn
Das sieht man aber nun wirklich nicht auf einen Blick. Mir ist nur bekannt, daß die Beziehung
ò0 ¥ e-x * xn-1 = (n-1)!
gilt (was man auch noch relativ einfach zeigen kann). Aber woher kommt das nn? Das würde mich auf alle Fälle noch interessieren.
Die interessanten Integrale von Deinem letzten Posting muß ich erst noch studieren...
Kay S. |
    
H.R.Moser,megamath

| | Veröffentlicht am Freitag, den 15. Februar, 2002 - 09:28: | 
|
Hi Kay,
Es ist mir ein wirkliches Anliegen, Dir bei der Lösung Deiner
wunderschönen Aufgabe behilflich zu sein, und ich hoffe, dass
die Beweislücke mit dem folgenden Beitrag ganz geschlossen
wird.
Ich erinnere an meinen letzten Beitrag und zitiere daraus Punkt 5 :
5.
J5 = int [ e^ (- a * x ) * x ^ (n -1) * dx ] ,
untere Grenze 0, obere Grenze unendlich.
n positiv ganz, a > 0
Es gilt:
J5 = (n-1)! / a ^ n
Dieses Integral kannst Du im Spezialfall a = n , wie ich in meinem
letzten Beitrag ausgeführt habe, zum Beweis Deiner Formeln benützen.
Der Spezialfall lautet in extenso :
J5* = int [ e^ (- n* x ) * x ^ (n -1) * dx ] = (n -1)! / n ^ n
untere Grenze 0, obere Grenze unendlich.
Diese Formel lässt sich relativ einfach beweisen, z.B.
auch mit vollständiger Induktion (Schluss von n auf n+1).
Lassen wir das auf sich beruhen !
Ende Zitat.
Ein einfacher Weg, J5 zu beweisen, ist der folgende:
Substitution a * x = u , a * dx = du ; eingesetzt ergibt
J5 = int [e^(-u) * (u/a)^(n-1) * 1/a * du ] =
=1 / a ^ n * int [e^(-u) * u ^(n-1) * du ]
untere Grenze u = 0, obere Grenze u = unendlich.
Das letzte Integral in u ist das von Dir erwähnte bekannte
Integral mit dem Resultat (n-1)!
Damit ist J5 und auch J5* hergeleitet, und wir haben hautnah erlebt,
woher die Potenz a^n bzw. n^n kommt.
Du erkennst das Prinzip:
Hänge den Hut von einem Haken zum andern, und versuche am Schluss,
einen besseren Zugang zum Problem zu erreichen.
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
H.R.Moser,megamath

| | Veröffentlicht am Freitag, den 15. Februar, 2002 - 20:35: | 
|
Hi Kay,
Mir ist noch eine weitere Methode zur Herleitung Deiner
zweiten Relation eingefallen, die ich Dir gerne hier vorlege.
Die Methode ist recht lehrreich und kann für analoge Fälle hilfreich sein.
Ausgangspunkt ist das Integral
M(a) = int [x ^ ( a -1) * dx ] mit a > 0.
Die Grenzen sind :
untere Grenze x = 0 , obere Grenze x = 1
Wir leiten dieses Integral n mal nach dem Parameter a ab ; es kommt
der Reihe nach:
M´(a) = int [ x^(a-1)* ln x ] * dx = - 1 / a^2
M´´ (a) = int [ x^(a-1)* (ln x)^2 ] * dx = 2! / a^3
………………………………………………………………………….
int [ x^(a-1)* (ln x) ^(n-1) ] * dx = ( - 1) ^ (n-1) * (n-1)! / a^n
Grenzen des Integrals: untere Grenze x = 0 , obere Grenze x = 1
Nun setzen wir a = n und erhalten:
int [ x^(n-1)* (ln x) ^(n-1) ] * dx = ( - 1) ^ (n-1) * (n -1)! / n^n
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Wir summieren dies von 1 bis n
und erhalten links unter einem einzigen Integral in den genannten Grenzen
wiederum eine unendliche geometrische Reihe mit dem Anfangsglied 1
und dem Quotienten q = x * lnx .
Als neuen Integrand erhalten wir die Summe S dieser Reihe, also
S = 1 / (1 – q) = 1 / (1 – x * ln x ) ; mithin gilt:
int [1 / (1 – x * ln x ) = sum ( - 1) ^ (n-1) * (n-1)! / n^n .
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Summation: n = 1.. unendlich
Integration: x = 0 .. unendlich
Wir erreichen das Ziel, wenn wir im Integral die Substitution
x = e ^(-t) , also ln x = - t , dx = - x * dt = - e^(-t)*dt ausführen.
Aus den Grenzen 0 und 1 entstehen zunächst die Grenzen null
und unendlich für t.
Kehrt man diese Grenzen um, so erzielt man den Ausgleich durch
Multiplikation des Integrals mit –1; schliesslich steht Deine
zweite Relation vor uns ; Bravo !
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Samstag, den 16. Februar, 2002 - 16:40: | 
|
Ja. In diesem Falle gilt sogar vereinfacht M(a)=1/a. Es ist doch schön zu sehen, wie sich ein schwieriges Problem aufklart!
Kay S. |
|