| Autor |
Beitrag |
    
nelly

| | Veröffentlicht am Sonntag, den 03. Februar, 2002 - 13:55: | 
|
Man bestimme den Schwerpunkt der Fläche mit der folgenden Berandung:
y=sin²x ,x=0, x=Pi, y=0 |
    
L.

| | Veröffentlicht am Sonntag, den 03. Februar, 2002 - 18:56: | 
|
Hi nelly,
Das kannst Du auch ohne Differentialgleichung rechnen. |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Sonntag, den 03. Februar, 2002 - 23:02: | 
|
Also, ersmal eine Zeichnung
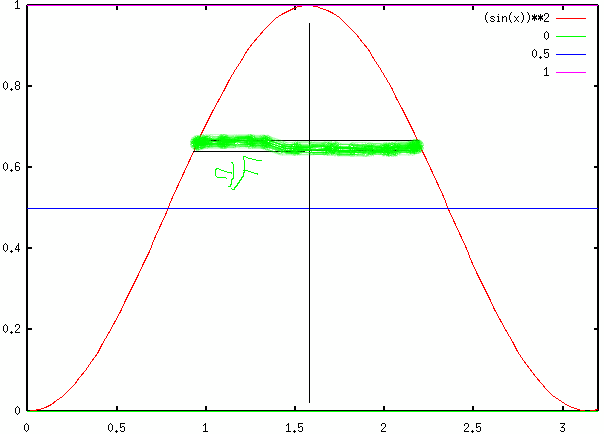
Dass die x-Koordinate des Schwerpunktes pi/2 ist
ist ja offensichtlich. Für die y-Koordinate Y müssen
die Momente der wagrecheten Flächenelemente dF die auch
Kraftelemente sind, im Gleichgewicht sein.
Die Momente dM sind (Y-y)*dF, und M = 0 muss gelten
M = ò0 1dM = ò0 1(Y-y)*dF
y = sin²x = (1-cos 2x)/2; 2y = 1 - cos 2x;
1-2y = cos 2x; x = 0.5*arccos(1-2y)
das x ist der Wert ausserhalb der umrandeten Fläche
das Für die Schwerpunktermittlung massgebliche dF ist
dF = dy*(pi - 2x) = dy*(pi - arccos(1-2y)
M = ò0 1(pi - arccos(1-2y))*(Y-y)*dy
Der schwierige Teil des Integrals ist mit
1) Subst. u = 1-2y
2) partielle Integration für (u-1)*arccos(u) [erstmal arccos intrgrieren]
3) Trig.subst für verbleibenden Integranden sqrt(1-w²)
lösbar
ò arccos(u)du = u*arccos(u) - sqrt(1-u²)
sodann brauch nur mehr M = 0 nach Y aufgelöst
zu werden. |
    
Gorn

| | Veröffentlicht am Montag, den 04. Februar, 2002 - 00:26: | 
|
Hallo, ich habe so etwas noch nie gerechnet,
ich möchte mal wissen, ob das richtig ist (ne Differentialgleichung hab ich übrigens auch nicht gebraucht)
Die nötigen Formeln können einer Formelsammlung entnommen werden, z.B. der hier:
www.fh-kaernten.ac.at/~pester/Stoecker/daten/part_6/node168.htm
Die Koordinaten des Schwerpunktes (a|b) einer Fläche im Bereich B errechnen sich nach:
a = 1/A ò(B)ò x dA = 1/A òyminymax òxminxmax x dxdy
b = 1/A ò(B)ò y dA = 1/A òyminymax òxminxmax y dxdy
wobei A = ò(B)òdA = òò dxdy
bedeutet.
Also:
der Bereich, über den zu integrieren ist, geht für x von 0 bis Pi
und für y von 0 bis y(x)=sin²(x), also integriere erst über y, dann über x:
A = òò dydx
A = ò0Piò0sin²(x) dydx
A = ò0Pi [y]0sin²(x) dx
A = ò0Pi sin²(x) dx, Stammfunktion von sin²(x) ist ½x - ¼sin(2x) (zur Probe ableiten!)
A = [½x - ¼sin(2x)]0Pi
A = ½Pi - ¼*0 - (0 - 0)
A = Pi/2
a = 1/A òxminxmax òyminymax x dydx
a = 2/Pi ò0Pi ò0sin²(x) x dy dx
a = 2/Pi ò0Pi x [y]0sin²(x) dx
a = 2/Pi ò0Pi x sin²(x) dx
Stammfunktion von x sin²(x) durch partielle Integration:
ò x sin²(x) dx = [x*(½x - ¼sin(2x))] - ò ( ½x - ¼sin(2x) ) dx
= [½x²-¼xsin(2x)] - [¼x²] + ¼ò sin(2x) dx
= [½x²-¼xsin(2x)- ¼x²] + [¼ * (-½) cos(2x)]
= [¼x²-¼xsin(2x) -cos(2x)/8]
also
a = 2/Pi [¼x²-¼xsin(2x) -cos(2x)/8]0Pi
a = 2/Pi [Pi²/4 - Pi/4 *0 - cos(2Pi)/8 - (0-0-cos(0)/8)]
a = 2/Pi [Pi²/4 - 1/8 - +1/8]
a = Pi/2
(War ja zu erwarten, da der Graph symmetrisch zu x=Pi liegt)
b = 1/A òxminxmax òyminymax y dydx
b = 1/A ò0Pi ò0sin²x y dy dx
b = 1/A ò0Pi [½y²]0sin²x dx
b = 2/Pi ò0Pi (½(sin(x))^4) dx
b = 2/Pi * ½[3x/8 -¼sin(2x) + 1/32 sin(4x) ]0Pi
b = 1/Pi * [3Pi/8 -0 + 0 -0 ]
b = 3/8 |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Montag, den 04. Februar, 2002 - 08:35: | 
|
SEHR elegant Gorn!
Ich muss zugeben, dass meine Ausbildung nicht U-Niveau hat und ich mit Mehrfachintegralen nichts zu tun hatte. Die Formel aus dem Stöcker kann ich allerdings verstehen: der S liegt dort wo ein Massepunkt mit dem Gesamtgewicht dasselbe Moment ausüben würde wie das Integral der Momente. Ich habe eben nach Momentengleichgewicht gesucht.
Bleibt die Frage ob nelly's eigentlicher Aufgaben"schwerpunk" Physikverständnis oder nur eine Übung mit Mehrfachintegralen sein sollte.
In letzterem Fall ist das Nachschlagen natürlich
"erlaubt". |
    
H.R.Moser,megamath

| | Veröffentlicht am Montag, den 04. Februar, 2002 - 09:53: | 
|
Hi allerseits,
Die vorgelegte Aufgabe zur Ermittlung der y-Koordinate b
des Flächen-Schwerpunktes ist sozusagen massgeschneidert für
den Einsatz einer Guldinschen Regel.
Wir benötigen dafür bloss zwei gewöhnliche Integrale,
die man Tabellen entnimmt oder auch mehr oder weniger bequem
von Hand rechnet, nämlich:
unbestimmtes int[(sin x)^2 * dx ] = ½ (x – sin x * cosx),
daraus
bestimmtes Integral J1 ,untere Grenze 0 , obere Grenze Pi :
J1 = ½ * Pi
unbestimmtes int[(sin x)^4 * dx ] = - ¼ (sin x)^3*cos x –3/8 cos x*sin x + 3/8*x
bestimmtes Integral J2 ,untere Grenze 0 , obere Grenze Pi :
J2 = 3/8 * Pi
Die von der Kurve und der x-Achse eingeschlossene Fläche A ist demnach
A = J1 = ½ * Pi
Das von der Kurve bei Rotation um die x-Achse erzeugte Volumen V ist demnach
V = Pi * J2 = 3/8 * (Pi) ^2.
Nach Guldin erhalten wir für die Ordinate b des Schwerpunktes S der
Fläche A die Gleichung:
V = 2*Pi * b * A
Auf der rechten Seite der Gleichung steht das Produkt
Länge des Weges des Schwerpunktes S bei Rotation um die x-Achse mal Fläche A.
Wir entnehmen der Gleichung das Schlussresultat
yS = b = 3/8 (Pi hat sich in Luft aufgelöst !)
°°°°°°°°°°°°°
Zu Guldin (nach Brockhaus)
Paul Guldin, schweizerischer Mathematiker aus St. Gallen (Rufname Habakuk) ,
1577-1643, Jesuit; Prof. in Wien und Graz.
Guldin verteidigte 1618 in einer Streitschrift die Einführung des Gregorianischen
Kalenders.
In seiner vierbändigen Arbeit über Kinematik
„Centrobaryca seu de centro gravitatis...“ ...sind neben zahlreichen
Flächen – und Volumenbestimmungen auch die nach ihm benannten Regeln enthalten.
Mit freundlichen Grüßen
H.R.Moser,megamath |
|