| Autor |
Beitrag |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Samstag, den 19. Januar, 2002 - 20:43: | 
|
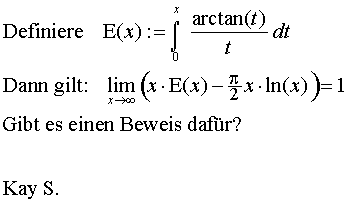 |
    
H.R.Moser,megamath

| | Veröffentlicht am Sonntag, den 20. Januar, 2002 - 18:27: | 
|
Hi Kay,
Ich habe die Gewohnheit angenommen, auf Deine interessanten
Aufgaben, die Du ins Board stellst, mit einem in einer näheren
Epsilonumgebung angesiedelten Problem zu reagieren .
Das ist echte Hilfe zu Selbsthilfe !
Diesmal lautet die Aufgabe so:
Die untere Grenze des Integrals J ist 0,die obere Grenze unendlich
Man beweise:
J = [int {arctan (ax) – arctan (bx)}/ x * dx ] = ½ * Pi * ln ( a / b )
Voraussetzung: a > 0, b > 0 .
Darf ich zum Abschluss noch eine Frage allgemeiner Art stellen.
Mich würde interessieren,woher die Aufgaben stammen, die Du ins
Board stellst .
Wer ist der Autor dieser recht anspruchsvollen Probleme ?
Für welches Ausbildungsniveau sind sie bestimmt und in welcher Form
werden sie veröffentlicht ?
Für potentielle Aufgabenlöser sind Fragen nach dem Umfeld wichtig,
insbesondere auch die Frage nach den Mitteln, die bei einer allfälligen
Lösung eingesetzt werden dürfen.
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Montag, den 21. Januar, 2002 - 22:49: | 
|
Hi MegaMath,
Das ist ja nett, daß Du auf meine Fragen immer sofort eine Gegenfrage bereithältst!
In diesem Fall hast Du wirklich ein hochinteressantes Integral gebracht. Mittels partieller Integration erhält man Integrale der Form
ò0 ¥ ln(x)/(c*x2 + 1) dx, wobei c von a und b abhängt. Ich konnte aber nicht direkt den von Dir angegebenen Wert ½ * p * ln(a/b) ableiten.
Interessanterweise steht obiges Integral im engen Zusammenhang mit der noch wenig erforschten Catalanschen Konstante. (Weißt Du mehr darüber?)
Jedenfalls kann ich den Zusammenhang zu meiner Aufgabe nicht ganz erkennen. Im Prinzip geht es doch (nach meiner Interpretation) um das asymptotische Verhalten der Funktionen E(x) und p/2 * ln(x).
Da die arctan-Funktion im Unendlichen quasikonstant ist (mit dem Wert p/2), verhält sich E(x) durch die Integration asymptotisch zu p/2 * ln(x), d. h. deren Differenz E(x) - p/2 * ln(x) geht gegen einen konstanten Wert.
Erstaunlicherweise ist dieser offensichtlich 0, aber warum?
Experimentiert man jetzt noch weiter und setzt diesen Rest dann noch in Zusammenhang zu x, so ergibt sich der ominöse Grenzwert 1/x, was in der gestellten Aufgabe zum Ausdruck kommt. Leider stecke ich an dieser Stelle fest, die Ableitungen zu untersuchen bringt's offensichtlich auch nicht.
Zu Deiner Frage, woher ich die Aufgaben habe. Einige der Probleme, die ich ins Board gestellt habe sind tatsächlich etwas kompliziert. Sie sind sozusagen aus meiner privaten Sammlung ungelöster Probleme, die mir irgendwann über den Weg gelaufen sind. Die Herkunft habe ich leider nicht in jedem Falle parat.
Kay S. |
    
H.R.Moser,megamath

| | Veröffentlicht am Dienstag, den 22. Januar, 2002 - 14:09: | 
|
Hi Kay,
Mein Dank und meine Anerkennung für Deine Ausführungen !
Ich schätze es sehr, wenn meine Arbeiten im Board auf Widerhall
stossen, besonders auch dann, wenn die Bemerkungen und Anregungen
auf profunde Fachkenntnisse hinweisen, wie es soeben der Fall war.
Es geht mir genau gleich :
Ueberall liegen ungelöste Probleme herum, die einen richtiggehend
verfolgen.Es bleibt offenbar nichts anderes übrig ,als sie zu lösen (!)
Im vorliegenden Fall braucht das jedenfalls noch seine Zeit.
Vorläufig etwas zu Catalan.
Rudimentäres zu Catalan
1.
ad personam:
Eugène Charles Catalan (1814-1894),belgischer Mathematiker
2:
Arbeiten zur Analysis u.a.:
Variablensubstitution bei Mehrfachachintegralen
3.
Arbeiten zur Zahlentheorie u.a.:
Bis heute unbewiesene Vermutung von Catalan :
die Zahlen 8 und 9 sind die einzigen natürlichen Zahlen
mit der Eigenschaft, dass sie aufeinanderfolgen und als
echte Potenzen geschrieben werden können:
8 = 2^3 und 9 = 3^2.
4.
Catalansche Gleichung
Eine exponentiell diophantische Gleichung mit Unbekannten im
Exponent:
x^m – y^n = 1
5.
Zur Catalan Konstante (nach Maple):
catalan Catalan's constant = sum((-1)^i/(2*i+1)^2,i=0..infinity)
evalf(Catalan) is approximately 0.915965594.
6.
Catalan-Zahl C(n)
z.B. Die Anzahl der Wege mit der Länge 2n in einem
(n x n) – Raster unterhalb der Hauptdiagonalen
Explizit erhält man für C(n)
C(n) = (2n)! / [(n+1)!*n!]
Die ersten 6 Catalanzahlen sind 1, 2 ,5 ,14 ,42,132.
Es gilt die Summendarstellung:
sum[C(n) * x ^ n] = f(x) mit
f(x) = {1 – wurzel [1- 4 x] } /{2 x }
Summe von 0 bis unendlich.
Beispiel mit Maple berechnen:
wähle x = ¼ und summiere von n = 0 bis infinity über
a(n) = (2n)! / [(n+1)!*n!] * ( ¼ ) ^ n
Resultat: Summe S = 2, wie auch aus der obigen
erzeugenden Funktion f(x) folgt.
Bis dann
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Dienstag, den 22. Januar, 2002 - 15:54: | 
|
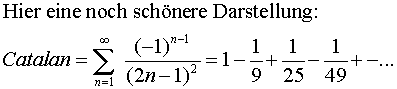 |
    
H.R.Moser,megamath

| | Veröffentlicht am Dienstag, den 22. Januar, 2002 - 16:44: | 
|
Hi Kay,
Ich schlage ein Privatissimum vor und zwar zum Thema
DILOGARITHMUS
Du findest im Archiv drei Arbeiten dazu unter dem Stichwort
„DILOGARITHMUS“.
Ich bin der Meinung, dass dieser Begriff und die zugehörige
Theorie für unsere Integralaufgaben nützlich sein werden.
Viel Vergnügen beim Studium !
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
H.R.Moser,megamath

| | Veröffentlicht am Dienstag, den 22. Januar, 2002 - 20:45: | 
|
Hi Kai,
Auch schön ist dies:
polylog (2,1) = - 1 / 48 * Pi ^ 2 + i * Catalan , oder:
dilog (2) = - 1 / 12 * Pi ^ 2 oder
dilog (3)+ dilog (-2) = 1 / 6 * Pi ^ 2 – ln(2) * ln(3) – i * ln(3)* Pi , oder
dilog (1/2) + dilog (-1/ 2) +dilog (3 / 2) =
= ¼ * Pi ^ 2 – ½ ln(2)^2 + ln(2)*ln(3/2) - i * ln (3/2 ) * Pi
u.s.w.
MfG
H.R.Moser,megamath |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Mittwoch, den 23. Januar, 2002 - 20:06: | 
|
Hi MegaMath,
Kennst Du bei der Gelegenheit vielleicht ein Additionstheorem für den Dilogarithmus?
Kay S. |
    
H.R.Moser,megamath

| | Veröffentlicht am Donnerstag, den 24. Januar, 2002 - 09:38: | 
|
Hi Kay,
Formeln zur dilog-Funktion (The Dilogarithm Function) sollten nur
in homöopathischen Dosen (in hoher Verdünnung) verwendet werden.
Eine solch verdünnte Formel will ich Dir gerne mitteilen ;
es handelt sich um ein Mini - Additionstheorem:
S = dilog ( 1+ i*y ) + dilog ( 1 – iy) = dilog ( 1+ y ^ 2 )
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Nachtrag
Uebrigens ist Maple imstande, das in meiner ersten Arbeit erwähnte Integral
formal zu berechnen:
Setze a = 2 , b =1, damit wird f :=arctan(2*x) - arctan(x); unbestimmtes Integral:
F:=int(f,x);
Resutat:
F:= - ½ I dilog(1-2 I x )+½ I dilog(1+2 I x ) + ½ I dilog(1- I x ) - ½ I dilog(1 + I x )
bestimmtes Integral, untere Grenze 0 ,obere Grenze N:
FN:= int(f, x = 0..N);
Resultat:
FN:= - ½ I dilog(1-2 I N )+½ I dilog(1+2 I N ) + ½ I dilog(1- I N ) - ½ I dilog(1 + I N)
bestimmtes Integral ,untere Grenze 0 ,obere Grenze unendlich
F*:= int(f, x = 0..infinity);
Resultat:
F* = ½ * Pi * ln(2)
°°°°°°°°°°°°°°°°°°°
BRAVO !
MfG
H.R.Moser,megamath |
|