| Autor |
Beitrag |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Mittwoch, den 09. Januar, 2002 - 19:54: | 
|
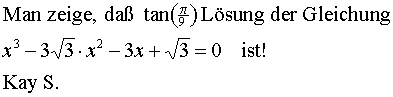 |
    
H.R.Moser,megamath

| | Veröffentlicht am Donnerstag, den 10. Januar, 2002 - 07:43: | 
|
Hi Kay,
Eine Zusatzaufgabe an Stelle einer Lösung !
Ich gestatte mir, Deine Aufgabe umzuformen und sie,
in einem etwas andern Gewande und kaschiert, erneut zu stellen.
Sei T = tan (Pi/9); man beweise, dass T die Relation
(1 + T ^ 2 ) ^ (3 / 2) + 6 * T ^ 2 – 2 = 0
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
erfüllt.
Besteht überhaupt ein Zusammenhang mit Deiner
einfachen Gleichung,und wenn ja,
in welcher Art ?
Mit freundlichen Grüssen
H.R.Moser,megamath. |
    
N.

| | Veröffentlicht am Donnerstag, den 10. Januar, 2002 - 17:48: | 
|
Hi Kay und Megamath,
erstmal zu Kays aufgabe:
Die Lösungen der oben genanten Gleichung sind:
x1=4*cos(10°)+Ö3
x2=4*cos(130°)+Ö3
x3=4*cos(250°)+Ö3
Auf wunsch wird die Gleichung algebraisch und von mir ausführlich im Board gelöst.
Es gilt hierbei,
x3=tan(p/9)=tan(20°)
Soweit erstmal...
Gruß N. |
    
H.R.Moser,megamath

| | Veröffentlicht am Donnerstag, den 10. Januar, 2002 - 21:38: | 
|
Hi N,
Besten Dank für Deine Bemühungen , alle Lösungen der
Gleichung von Kay zu ermitteln.
Eine ausführliche Herleitung würde mich sehr interessieren;
von detaillierten Ausführungen können wir alle nur
profitieren.
Uebrigens steht die von mir aufgestellte Gleichung in engem
Zusammenhang mit der Kreisteilungsgleichung für n = 9
(Berechnung des regulären Neunecks).
Ich würde mich sehr freuen, wenn im gleichen Umgang auch
diese Gleichung gelöst wird.
Besten Dank und freundliche Grüsse
H.R.Moser,megamath. |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Freitag, den 11. Januar, 2002 - 12:42: | 
|
Hi N & MegaMath,
An einer algebraischen Lösung der Gleichung wäre ich auch sehr interessiert. Ich wäre auch dankbar, wenn ihr den Zusammenhang zur Kreisteilungsgleichung noch ausführlicher posten könntet. Zur Aufgabe fallen mir noch zwei zusätzliche Fragen ein:
1. Als Lösung einer kubischen Gleichung muß es doch einen geschlossenen Wurzelausdruck für tan(p/9) geben (Galois-Theorie?). An anderer Stelle habe ich aber erfahren, daß ein solcher speziell für tan(p/9) nicht existiert. Tatsächlich geben auch Wertetafeln für tan(p/n) nur für n=1-6,8,10,12,16,20,24 exakte Werte an.
2. Handelt es sich eigentlich um eine algebraische Zahl? Voraussetzung dafür ist doch eine Polynomgleichung mit ganzzahligen Koeffizienten. Ich habe es aber nicht geschafft, die Wurzeln zu eliminieren.
Mit freundl. Gruß
Kay |
    
H.R.Moser,megamath

| | Veröffentlicht am Freitag, den 11. Januar, 2002 - 14:25: | 
|
Hi Kay,
Die von Dir zur Diskussion gestellte Zahl
T = tan (Pi / 9) erfüllt die folgende Gleichung
sechsten Grades:
x ^ 6 – 33 x ^ 4 + 27 x ^ 2 – 3 = 0
(bitte kontrollieren !)
Ich komme auf die Angelegenheit zurück .
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Orion

| | Veröffentlicht am Freitag, den 11. Januar, 2002 - 16:29: | 
|
Hallo Kai, N., megamath:
Wegen der Verdreifachungsformel des tan
hat man unmittelbar
tan(pi/3) = sqrt(3)= (3x - x^3)/(1 - 3x^2)
und daraus durch Umordnen die fragliche Polynomgleichung.
Uebrigens ist
(x^3-3sqrt(3)x^2-3x+sqrt(3))(x^3+3sqrt(3)x^2-3x-sqrt(3)) = x^6-33x^4+27x^2-2.
Auf letzteres Polynom komme ich, wenn ich
cos(2pi/9) = (1-x^2)/(1+x^2)
sowie die Verdreifachungsformel für cos anwende.
mfg
Orion |
    
H.R.Moser,megamath

| | Veröffentlicht am Freitag, den 11. Januar, 2002 - 18:18: | 
|
Hi Orion, hi N, hi Kai
Orion hat die anstehenden Probleme auf wundersame Weise gelöst !
Ich möchte ihm zu seiner rettenden Idee gratulieren.
Die von mir angegebene Gleichung sechsten Grades mit
ganzzahligen Koeffizienten zeigt, dass die inkriminierte Zahl T
algebraisch ist.
Damit ist eine weitere Frage von Kai beantwortet.
Es könnte lehrreich sein, den genauen Zusammenhang mit der
betreffenden Kreisteilungsgleichung herzustellen.
Wenn ich Zeit aufbringe und der Wunsch danach immer noch
Besteht, werde ich dies besorgen.
Mit freundlichen Grüßen an alle Beteiligten
H.R.Moser,megamath |
    
H.R.Moser,megamath

| | Veröffentlicht am Freitag, den 11. Januar, 2002 - 22:13: | 
|
Hi allerseits,
Hier die versprochenen Ausführungen zur Kreisteilung
A]
Kreisteilungsgleichung: x^n – 1 = 0.......................................................(I)
Die n Lösungen sind die so genannten n-ten Einheitswurzeln (EW).
Mit E = cos(2*Pi /n) + i sin(2*Pi/n) erhält man alle n Lösungen
in der Gestalt:
1 = E ^ 0, E = E^1 , E^2 , E^3 ,......…, E^(n-.1)……………………….(II)
N.B. E steht für epsilon.
Mit E^ (-1) = = cos(2*Pi /n) - i sin(2*Pi/n) erhält man die Relation
E ^(- k ) = E ^ ( n – k ) ......................................................................…(III)
Zerlegung der linken Seite der Gleichung (I) in zwei Faktoren
(x-1) * [ x ^ (n-1) + x ^ (n-2) +x ^ (n-3)+…….+ x + 1 ] = 0 ...............(IV)
Die (n-1) Potenzen E^1,E^2,...E^(n-1) aus (II) sind gerade die n-1
verschiedenen Lösungen der Gleichung (n-1)-ten Grades
x ^ (n-1) + x ^ ( n - 2) +....................... + x + 1 = 0........................................(IV)
Insbesondere ist für x = E:
E ^ (n-1) + E ^ ( n - 2) +....................... + E + 1 = 0........................................(V)
Es gilt der Satz
Die Summe der (n-1) von 1 verschiedenen n-ten EW ist gleich minus eins !
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
B]
Der Fall n =9
Hier ist E = cos(2*Pi / 9) + i sin(2*Pi 9)
Wegen 1 = E^9 = (E^3)^3 gilt :
Wenn E eine neunte EW ist, so ist E^3 eine dritte EW.
Wenn diese dritte EW nicht 1 ist, also E nicht selber dritte EW ist., so gilt:
E ^ 6 + E ^ 3 + 1 = 0.........................................................................................(VI)
(VI) bleibt richtig, wenn darin E ersetzt wird durch
E ^ 2 , E ^ 4, E ^ 5 , E ^ 7, E ^ 8
In der letzten Zeile haben wir die neben E noch vorhandenen Lösungen
der Gleichung (VI) vorliegen.(richtig gezählt sind es 6 an der Zahl).
Wegen (III) gilt E ^ (- 3) = E ^ (9 – 3) = E ^ 6, sodass (VI) auch so
geschrieben werden kann:
E ^ 3 + E ^ (- 3 ) + 1 = 0..................................................................................(VII)
Nun liegt die Substitution
y = E + 1/E nahe; für y ^3 kommt die Beziehung:
y ^ 3 = E ^3 + 3* ( E + 1/E ) + E ^ (-3) = E^3 + 3*y + E^ (-3),
damit kommt für die Gleichung (VII) die Gleichung dritten Grades in y:
y ^ 3 – 3 y + 1 = 0 ............................................................................................(VIII)
°°°°°°°°°°°°°°°°°°°
von der wir alle drei Lösungen y1,y2,y3 kennen; diese lauten:
y1 = E + 1/E = 2* cos(2Pi/9)
y2 = 2* cos(4*Pi/9)
y3 = 2 cos (8 Pi/9) = - 2*cos(Pi/9)
Zwei Lösungen sind positiv, eine negativ.
Uebrigens stellt y2 die Seitenlänge des regulären 18-Ecks mit
dem Einheitskreis als Umkreis dar.
C]
Spielereien mit der Lösung y3 aus Teil B]
Wir schliessen
cos(Pi/3) = - ½ *y
Sei tan(Pi/9) = T, dann ist
[cos(Pi/9) ] ^ 2 = 1 / ( 1+T ^2 ) , also ¼ * y^2 = 1 / (1+T^2),
y = 2 / wurzel(1+T^2)
Eingesetzt in die Gleichung (VIII) und diese bruchfrei gemacht:
8 – 6* ( 1 + T ^ 2 ) + ( 1 + T ^ 2 ) ^(3/2) = 0 oder
( 1 + T ^ 2 ) ^ (3 / 2 ) = 6 T ^ 2 – 2 ; quadriert man dies, so erhält man die
früher erwähnte Gleichung 6.Grades.
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
Niels

| | Veröffentlicht am Samstag, den 12. Januar, 2002 - 10:36: | 
|
Hallo allerseits,
hier nun noch zum Abschluß die ausführliche Lösung von Kay's Gleichung 3. Grades.
x^3-3*sqrt(3)x^2-3x+sqrt(3)=0..................(I)
Wenn man nun dieb ursprüngliche Gleichung (I) mit 27 multipliziert und die 3. und 2. Potenz isoliert erhält man:
27x^3-81*sqrt(3)x^2=81x-27*sqrt(3)
Über den Ansatz:
(s+t)^3=s^3+3s^2t+3st^2+t^3
Und Koeffizientenvergleich folgt:
S=3x und t=-3*sqrt(3)
Aus den obigen Ansatz und "kubischer Ergänzung" folgt:
(3x-3*sqrt(3))^3=324x-108*sqrt(3)
Durch die Substitution:
y=3x-3*sqrt(3)
erhalten wir die sogenante reduzierte kubische Gleichung:
y^3=108y+216*sqrt(3).........................(II)
Durch Die Substitution y=u+v und durch die Anwendung des Satzes von Vieta erhalten wir die sogenante quadratische Resolvente:
z^2-216*sqrt(3)z+46656=0....................(III)
Da ihre Diskriminante D=sqrt(34992-46656)=sqrt(-11664)<0 ist besitzt diese quadratische Resolvente 2 Komplexe Lösungen und damit besitzt die kubische Gleichung 3 reelle Lösungen(->Casus irreducibilis)-nämlich die von mier oben genannten.
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°^°°°°°°^°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
So, Der Rest folgt später....
Gruß N. |
    
Niels

| | Veröffentlicht am Samstag, den 12. Januar, 2002 - 11:17: | 
|
Hallo Kay, megamath und Orion,
Nun folgt der 2. Teil:
Wir gehen von der quadratischen Resolvente aus:
z^2-216*sqrt(3)z+46656=0....................(III)
Die Lösungem der Gleichung sind:
Z1=108*sqrt(3)+sqrt(11664)i
Z2=108*sqrt(3)-sqrt(11664)i
Da wir aber bei jeder Lösung noch die 3. Wurzel ziehen müssen, müssen wir den Satz v. Moivre anwenden-dazu brauchen wir nen Betrag von Z und das Argument von Z- den Winkel Phi.
|z1|=|z2|=216
=>cubrt(|z1|)=6
cos(phi)=108*sqrt(3)/216=(1/2)*sqrt(3)
=>phi=30°
Damit ergeben sich dank Moivre - und Cardano - die 3 reelle Lösungen für y
y1=12*cos(10°)
y2=12*cos(130°)
y3=12*cos(250°)
Durch die Rücksubstitution von y erhält man die 3 reellen Lösungen für x wie ich sie oben angegeben habe.
x1=4*cos(10°)+sqrt(3)
x2=4*cos(130°)+sqrt(3)
x3=4*cos(250°)+sqrt(3)
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Übrigens hier noch ein passender Link zum Thema:
http://www.mathematik-online.de/F88.htm#Galois
Gruß N. |
    
H.R.Moser,megamath

| | Veröffentlicht am Samstag, den 12. Januar, 2002 - 18:09: | 
|
Hi Niels,
Für Deine ausgezeichnete Arbeit möchte ich
Dir meine Anerkennung und meinen Dank ausdrücken.
Die von Kay gestellte Aufgabe zieht einen langen
Rattenschwanz nach sich.
Das ist gut so.
Eine intensive Beschäftigung mit ein und demselben Problem
aus ganz verschiedenen Blickrichtungen mit unterschiedlichen
Methoden zeigt ,wie interessant unser Fach ist,
dies mindestens solange die Schlussresultate übereinstimmen.
Ich habe den Eindruck,dass das letzte Wort zu dieser schönen Aufgabe
noch nicht gesprochen ist und eine Dauersendung daraus entstehen könnte.
Nur nebenbei: wie stehen die Dinge im Fall n = 11,
ist z = tan(Pi/11) eine algebraische Zahl wie T = tan (Pi/9) ?
Zunächst aber eine einfachere Aufgabe, welche auch von Abiturienten
gelöst werden kann.
Beweise:
tan 20° * tan 40° * tan 60° * tan 80° = 3
(also schon wieder tan 20° ! )
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Samstag, den 12. Januar, 2002 - 20:22: | 
|
An alle Beteiligten,
Ich hätte wirklich nicht gedacht, daß meine einfache Gleichung soviel Echo hervorruft, deshalb herzlichen Dank an alle, die hier viel Zeit investiert haben.
Nach dem Beitrag von Orion über die Winkelverdreifachung habe ich mal ins Tafelwerk geschaut - und einen verblüffenden Zugang zur Lösung all unserer Problemen gefunden: ein Additionstheorem!
Es gilt nämlich: tan(x + y) = (tan(x) + tan(y))/(1 - tan(x)*tan(y))
Idee: Theorem auf Summen mit mehr als 2 Summanden anwenden, z B.
tan(3x) = tan(2x + x) = (tan(2x) + tan(x))/(1 - tan(2x)*tan(x)).
Nun ersetzen wir tan(2x) auch entsprechend. Setzt man als Unbekannte z = tan(x), erhält man eine Gleichung in Abhängigkeit von z.
Das hätte man auch bei tan(p/9) tun können, man hätte sofort die Gleichung
x6 - 33x4 + 27x2 - 2 = 0 erhalten.
Das Interessante: Das Verfahren kann man auf alle natürlichen n mit tan(p/n) ausdehnen, in dem man einen bekannten tan-Wert aufspaltet und danach mehrmals das Additionstheorem anwendet!
Für den von MegaMath angegebenen Wert tan(p/11) habe ich beispielsweise die Gleichung
x10 - 55x8 + 330x6 - 462x4 + 165x2 - 11 = 0 erhalten!
Des weiteren für tan(p/7) die Gleichung
x8 - 20x6 + 14x4 + 28x2 - 7 = 0
Interessant ist die Ähnlichkeit:
Man erhält offensichtlich immer biquadratische Polynome mit recht vielen reellen Nullstellen.
Für Sinus und Kosinus kann man ähnliche Überlegungen anstellen.
An der Stelle eine kleine Vermutung:
Sei q eine rationale Zahl. Dann sind sin(q*p), cos(q*p) und auch tan(q*p) (falls nicht gerade die Polstellen getroffen werden) allesamt algebraische Zahlen!
Bitte um Überprüfung.
Kay S. |
    
Niels

| | Veröffentlicht am Sonntag, den 13. Januar, 2002 - 14:08: | 
|
Hallo Kollegen,
vielen Dank Megamath für deine Anerkennung meiner Leistung!(obwohl ich im Gegensatz zu Orion nicht so viel geleistet habe....)
Dennoch ist ein Lob von dir immer ein besonderes Lob.
Nun zu deiner netten Aufgabe:
tan20°*tan40°*tan60°*tan80°...............(I)
Weil gilt:
tan60°=sqrt(3)
folgt:
sqrt(3)*tan20°*tan40°*tan80°..........(II)
Nun setzen wir für
tan40°=tan(60°-20°)=(sqrt(3)-tan20°)/(1+sqrt(3)*tan20°)
tan80°=tan(60°+20°)=(sqrt(3)+tan20°)/(1-sqrt(3)*tan20°)
in(II) ein und erhalten:
sqrt(3)((3*tan20°-tan^3(20°))/(1-3*tan^2(20°))).......(III)
nun entspricht aber der Term:
((3*tan20°-tan^3(20°))/(1-3*tan^2(20°)))=tan(3*20°)=tan(60°)=sqrt(3)
Diese Tatsache in (II) eingesetzt führt zur folgender Tatsache:
sqrt(3)*sqrt(3)=3
D.h
tan20°*tan40°*tan60°*tan80°=3
Wie Megamath behauptete-
q.e.d
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Über Kay's Kommentare muß ich erstmal grübeln...
Gruß N. |
    
Orion (Orion)

| | Veröffentlicht am Sonntag, den 13. Januar, 2002 - 15:50: | 
|
Kay :
Wenn q = m/n rational, so gilt
cos(q*PI) = Re(z^m) = (z^m + 1/z^m)/2
sin(q*PI) = Im(z^m) = (z^m - 1/z^m)/(2i)
wobei z := exp(PI*i/n) wegen z^n + 1 = 0
algebraisch ist. Dies trifft also auch für
die oben genannten (reellen) Zahlen zu.
mfg
Orion |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Montag, den 14. Januar, 2002 - 14:27: | 
|
Hi Orion,
Ein interessanter Ansatz. Wie sieht es aber mit tan(p/n) aus? Wegen tan(p/n) = sin(p/n)/cos(p/n) genügt es zu zeigen, daß der Quotient zweier algebraischer Zahlen wieder algebraisch ist. Das ist aber nicht ganz trivial.
Gruß, Kay |
    
Niels

| | Veröffentlicht am Montag, den 14. Januar, 2002 - 16:51: | 
|
Hallo zusammen,
in der Tat Kay ist es so, dass gilt:
Cos(x) ist eine algebraische Zahl=>cos(x/n) ist eine algebraische Zahl[n ist eine ganze Zahl ungleich Null]
Weiter kann man zeigen, das gilt:
Wenn cos(x) ist algebraisch dann ist sin(x) ebenfals algebraisch.
Summen, Produkt und invers algebraische Zahlen sind wieder algebraisch.
Mit diesen Hilfssätzen kann man deine Behaubtungen beweisen.
Gruß N. |
|