| Autor |
Beitrag |
    
Bryan (Bryan)

| | Veröffentlicht am Dienstag, den 07. August, 2001 - 15:47: | 
|
Hallo !
Wer kann mir bei den folgenden Aufgaben helfen ?
1. Gegeben ist f(x,y)=x*y-x-y betrachtet auf dem Einheitskreis
Gesucht: a)Begründen Sie, warum f auf dem Einheitskreis ein globales Extrema besitzt.
b)Berechnen Sie alle möglichen Extrema von f, bezogen auf den Einheitskreis, und bestimmen Sie unter diesen die globalen Extrema (mit Begründung).
2. Gegeben ist F(x,y)=(x^2+y , x*y+y-x)
Gesucht: a)Prüfen Sie ob F ein Gradientenfeld ist (mit Begründung).
b)Die Kurve Gamma sei definiert als der Viertelkreisbogen von (0,1) nach (-1,0)
Berechnen Sie das Arbeitsintegral von F entlang der Kurve Gamma.
Für eine Lösung mit Lösungsweg wäre ich sehr dankbar !
mfg
Bryan |
    
Fern

| | Veröffentlicht am Dienstag, den 07. August, 2001 - 17:19: | 
|
Hallo Bryan,
Es würde mich interessieren, was diese Aufgaben mit Funktionentheorie zu tun haben! |
    
Fern

| | Veröffentlicht am Dienstag, den 07. August, 2001 - 19:49: | 
|
Hallo Bryan,
Ich verstehe das mit der Funktionentheorie zwar noch immer nicht, habe aber mal die zweite Aufgabe gelöst:
F ist ein Gradientenfeld falls es eine Funktion f gibt, so dass gilt:
F = Ñf
==========
F ist dann "konservativ" und f heißt Potenzialfunktion von F.
Falls F konservativ ist, muss gelten:
¶P/¶y = ¶Q/¶x
wobei P(x,y) und Q(x,y) die Komponenten des Vektorfeldes F(x,y) bedeuten.
=====================
Unser Beispiel:
F = (x² + y; x*y + y -x) also
¶P/¶y = 1
¶Q/¶x = y - 1
also NICHT GLEICH: Es besteht keine Potenzialfunktion.
Schade, denn dann wäre das Arbeitsintegral leicht als Differenz des Potenzials an den Endpunkten des Weges zu berechnen.
So aber müssen wir das Linienintegral
W = ò Pdx + Qdy berechnen.
Dazu brauchen wir eine Parameterdarstellung des Weges:
(Dieser ist nicht ganz eindeutig definiert, ich nehme aber an, es sei der Viertelkreis mit Mittelpunkt im Ursprung gemeint)
x = 1*cos(t)
y = 1*sin(t)
wobei t von p/2 bis p läuft.
also: dx = -sin(t)*dt und dy = cos(t)*dt
Wir substituieren:
P = x²+y = cos²(t) + sin(t)
Q = xy +y -x = cos(t)*sin(t) + sin(t) -cos(t)
W = òp/2 p[cos²(t)*sin(t) +sin(t)*cos(t)-cos²(t)-cos²(t)*sin(t)-sin²(t)]*dt
= -òp/2 p [1 - sin(t)*cos(t)]*dt = ½*cos²(t) - t |p/2p
W = -½ - p/2
=====================
Falls ich mich nicht verrechnet habe.
===================================== |
    
Bryan (Bryan)

| | Veröffentlicht am Dienstag, den 07. August, 2001 - 19:58: | 
|
Hallo Fern !
Erst mal vielen Dank für die schnelle Antwort !
Ich weiß das die Aufgaben nicht unbendingt etwas mit Funktionentheorie zu tun haben, aber ich wußte nicht wo ich sie sonst hätte rein schreiben sollen !
mfg
Bryan |
    
mrsmith

| | Veröffentlicht am Mittwoch, den 08. August, 2001 - 09:39: | 
|
hallo Bryan,
funktionentheoretische begruendung von
aufg. 1 a)
f(x,y) = x*y -x -y laesst sich, unter der voraussetzung, dass z = x+iy gilt, schreiben als f(x,y) = Re[ (1/2i)z^2 - (1-i)z ].
damit ist f der realteil eines polynoms in z. da polynome ganze funktionen sind, ist f in der ganzen komplexen ebene C stetig. der einheitskreis ist eine abgeschlossene teilmenge von C. d.h. f nimmt auf dem Einheitskreis Minimum und Maximum an.
viele gruesse mrsmith |
    
Fern

| | Veröffentlicht am Mittwoch, den 08. August, 2001 - 09:52: | 
|
Hallo Bryan,
Jetzt zur ersten Aufgabe:
f(x,y)= xy-x-y
Globale Extrema auf dem Einheitskreis gesucht.
=======================
Eine Parameterdarstellung des Einheitskreises ist:
x = cos(t)
y = sin(t)
für 0 £ t £ 2p
======================
Dies substituieren wir in f(x,y) und erhalten:
g(t) = cos(t)*sin(t) - cos(t) -sin(t) für diese Funktion suchen wir nun die Extrema:
g'(t) = cos²(t) - sin²(t) +sin(t) - cos(t)
g'(t) = 0 ist erfüllt für t = 0, p/4, p/2, (5/4)p
Für jeden dieser 4 Punkte müssen wir nun f(x,y) oder g(t) bestimmen:
g(0) = -1--------------------------- glob. Min.
g(p/4) = ½ - Ö2 = -0,914...--------- (lok. Max)
g(p/2) = -1 -------------------------glob. Min.
g(5p/4) = ½ + Ö2 = 1,914...-------- glob. Max.
==========================
In x und y Koordinaten ausgedrückt:
(1; 0; -1) .......... glob. Min.
(½Ö2; ½Ö2; ½ - Ö2)
(0; 1; -1) ........... glob. Min.
(-½Ö2; -½Ö2; ½ + Ö2) ......... glob. Max.
Also: ein glob. Maximum und zwei globale Minimastellen.
================================
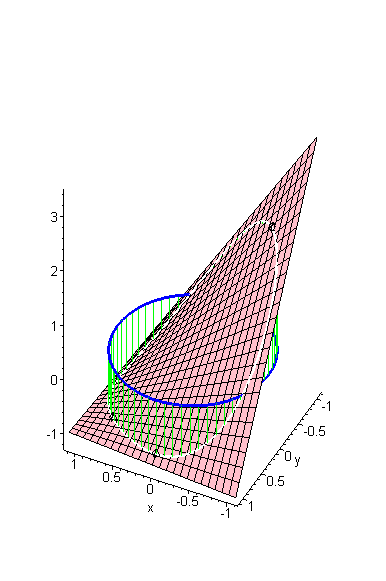
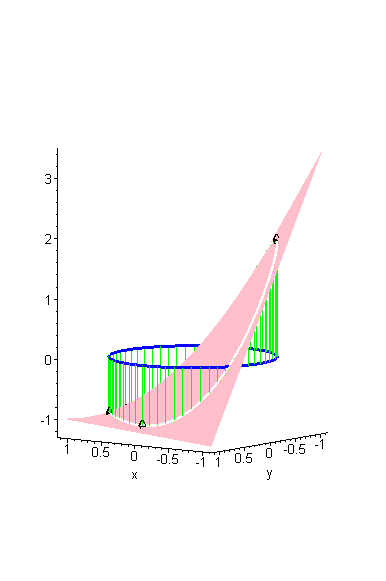
Ich habe dazu eine Skizze gemacht, die ich in 2 Ansichten zeige:
Der blaue Kreis ist der Einheitskreis in der x-y-Ebene, über (unter) dem wir einen Zylinder (grüne Mantellinien) errichten.
Schnitt mit der Fläche f(x,y) ist die weiße Kurve auf der die 4 Extrempunkte eingezeichnet sind.
Beachte: Die weiße Kurve hat zwischen den beiden globalen Minima eine kleine Delle, so dass der Punkt, der dem Max diametral gegenüber liegt, ein lokales Maximum darstellt. (Dies versuche ich im 2. Bild zu verdeutlichen).
(z-Werte überhöht dargestellt).
=================
Gruß, Fern |
    
Bryan (Bryan)

| | Veröffentlicht am Mittwoch, den 08. August, 2001 - 14:48: | 
|
Hallo Fern !
Noch mal vielen Dank für die ausführliche Lösung. Die Skizzen waren auch sehr hilfreich.
Allerdings hätte ich da noch ein paar Fragen zur ersten Aufgabe.
Gibt es nicht eine einfachere Möglichkeit zu beweisen, dass f Extremwerte besitzt ohne sie direkt auszurechnen? In Teil a ist nur die Begründung gesucht.
Zum Beispiel über die Definition:
f hat in x0eD ein globales Minimum, falls f(x)>=F(x0) für alle xeD
(Definition globales Maximum analog)
Warum haben in deiner Lösung die Extremwerte in x und y Koordinaten drei Werte anstatt zwei (x,y) ?
Ich vermute mal du hast die Skizzen mit Maple erstellt. Könntest du mir vielleicht verraten wie du sie ertellt hast (vor allem die grünen Mantellinien und die weiße Kurve) !?
Ist es vielliecht auch möglich, die Extrema mit dem Gradienten und der Hesse Matrix zu berechnen?
mfg
Bryan |
    
mrsmith

| | Veröffentlicht am Mittwoch, den 08. August, 2001 - 15:13: | 
|
hallo bryan,
zitat: "Zum Beispiel über die Definition:
f hat in x0eD ein globales Minimum, falls f(x)>=f(x0) für alle xeD
(Definition globales Maximum analog)"
in dieser definition kommt x0 vor. wenn man x0 kennt, kann man so vorgehen. dann hat man aber die position des extremwertes schon ausgerechnet.
um die existenz von extremwerten zu beweisen braucht man:
1) f ist stetig
2) der definitionsbereich D von f ist abgeschlossen
ohne beide voraussetzungen ist es nicht moeglich die existenz von extrema zu beweisen.
(funktionentheorie braucht man aber nicht.)
gruss mrsmith. |
    
Fern

| | Veröffentlicht am Mittwoch, den 08. August, 2001 - 17:16: | 
|
Hallo Bryan,
Da ja die Extrema über dem Kreis und nicht über der Kreisfläche gesucht sind, reduziert sich die Aufgabe auf das Aufsuchen der globalen Extrema der Funktion g(t), also einer Funktion von einer Variablen.
Für eine solche Funktion gilt der Satz:
Falls f stetig auf dem Intervall [a, b] ist, so hat f ein absolutes (= globales) Maximum und ein absolutes Minimum auf diesem Intervall.
Beachte: dies besagt nicht, dass nur ein einziges Max. oder Min. besteht.
In unserem Beispiel liegen zwei Punkte auf einer Höhe von -1, daher zwei globale Minima.
===============
Die Hesse-Matrix zu verwenden hieße mit Kanonen auf Spatzen zu schießen.
Dies wird verwendet, falls man Extrema über einem Gebiet G der x-y-Ebene sucht.
================================
Der Maple code: (mit Maple6)
restart:with(plots):
z:=x*y-x-y;
> p1:=plot3d(z,x=-1.1..1.1,y=-1.1..1.1,color=pink,axes=framed,orientation=[135,52]):
> xt:=cos(t):
> yt:=sin(t):
> p2:=spacecurve([xt,yt,0],t=0..2*Pi,color=blue,thickness=3):
> zt:=subs({x=xt,y=yt},z);
> p3:=spacecurve([xt,yt,zt],t=0..2*Pi,color=white,thickness=3):
> p4:=pointplot3d({[1,0,-1],[0,1,-1],[0.707,0.707,-0.914313],[-0.707,-0.707,1.914313]},color=black,symbolsize=20,symbol=CIRCLE):
> numL:=60:
> for i from 1 to numL do
> t:=i/numL*2*Pi;
> lines[i]:=plottools[line]([xt,yt,0],[xt,yt,zt],color=green,linestyle=1);
> end do:
> display({seq(lines[i],i=1..numL)},p1,p2,p3,p4);
===============================
Gruß, Fern |
    
Bryan (Bryan)

| | Veröffentlicht am Mittwoch, den 08. August, 2001 - 18:41: | 
|
Hallo Fern !
Die Lösung ist mir jetzt klar geworden. Auch der Maple Code funktioniert mit ein paar Änderungen bei mir (ich benutze Maple 5).
Die beiden Aufgaben sind aus einer Klausur, allerdings ist mir immer noch nicht ganz klar was man zur Aufgabe 1a) als Lösung schreiben sollte.
Vielen Dank für die Bemühungen !
Auch bei mrsmith möchte ich mich bedanken !
mfg
Bryan |
    
Fern

| | Veröffentlicht am Mittwoch, den 08. August, 2001 - 19:57: | 
|
Hallo Bryan,
Ich bin mir immer noch nicht sicher ob mit Einheitskreis der Kreis oder die Kreisfläche gemeint ist.
Falls "Kreis", so gilt der oben angeführte blaue Satz für g(t).
g(t) = cos(t)sin(t) - cos(t) - sin(t) ist eine stetige Funktion und das Intervall für
t ist abgeschlossen: [0; 2p].
Also muss ein globales Max und ein globales Min auf dem Kreis bestehen.
==============
Falls "Kreisfläche", so gilt folgender Satz:
Es sei f(x,y) eine stetige Funktion, definiert auf einem abgeschlossenen und beschränkten Gebiet D der x-y-Ebene, dann gibt es:
1) Mindestens einen Punkt in D wo f(x,y) einen maximalen Wert annimmt.
2) Mindestens einen Punkt in D wo f(x,y) einen minimalen Wert annimmt.
===========================
Unsere Funktion f(x,y) = x*y - x - y ist für alle Punkte der Kreisfläche definiert und ist dort stetig.
Die Einheitskreisfläche ist ein abgeschlossenes, beschränktes Gebiet,
ergo: es muss sowohl ein globales Maximum wie auch ein globales Minimum bestehen! (aber nicht notwendigerweise auf dem Rand).
============================
Anmerkung:
"abgeschlossen" heißt: das Gebiet enthält alle seine Randpunkte.
"beschränkt" heißt: das Gebiet D ist Teilgebiet einer abgeschlossenen Kreisfläche.
===================================
Nachsatz: Der Beweis der blauen Sätze ist etwas umfangreich und ist in Büchern der Analysis nachzulesen.
Gruß Fern |
    
Bryan (Bryan)

| | Veröffentlicht am Donnerstag, den 09. August, 2001 - 13:01: | 
|
Hallo Fern !
Ich weiß leider auch nicht ob es sich bei der ersten Aufgabe der Kreis oder die Kreisfläche gemeint ist. Die Aufgabe habe ich orginal aus einer Klausur abgeschrieben, dort stehen keine weiteren Hinweis ob Kreis oder Kreisfläche. Ich denke mal das wäre dann etwas was man in der Klausur fragen müßte.
Ich denke aber mal eher, dass es sich um die Kreisfläche handelt, da das eher zum Stoff der Vorlesung passt. Denn dann müßte ich doch die Hesse-Matrix anwenden, oder ?
Den obigen Satz über die Kreisfläche habe ich auch in der Vorlesung gehört.
Die Extrema in dieser Aufgabe sind doch bei der Kreisfläche dann zufällig auch die des Kreises, oder ?
mfg
Bryan |
    
H.R.Moser,megamath.

| | Veröffentlicht am Donnerstag, den 09. August, 2001 - 13:07: | 
|
Kali mera,
Zurück aus den Ferien, stelle ich mit Genugtuung fest ,
dass in der Zwischenzeit von den "Daheimgebliebenen"
intensiv und erfolgreich recht anspruchsvolle
Aufgaben bearbeitet wurden.
Besonders gut gefallen hat mir die Lösung mit Bildern
von Fern der hier vorliegenden ersten Aufgabe von Bryan.
Dazu möchte ich eine Kleinigkeit beisteuern
Wir betrachten die Niveaulinien der Fläche
z = f(x,y) = x * y - x - y .
Setzt man z = c , so erhält man als Niveaulinien eine Schar
Normalhyperbeln. x * y - x - y = c.
Der gemeinsame Mittelpunkt der Hyperbeln ist der Punkt
M(1/1), die Geraden a1: y = 1 und a2 : x = 1 sind die Asymptoten.
Wählt man diese Asymptoten als Achsen x' , y' eines parallel
verschobenen Koordinatensystems, so lautet die Gleichung
der Schar:
x' * y' = c + 1 = d.
Die Scheitel der Hyperbeln liegen auf der Geraden y = x : für
die Halbachse a gilt:
a = wurzel(2*d) = wurzel[2*(c+1)]
Die vorgelegte Extremalaufgabe kann nun auch mit der
Methode der berührenden Niveaulinien gelöst werden, indem
man diejenigen Niveaulinie heraussucht, welche den Einheitskreis k:
x^2 + y ^2 = 1 b e r ü h r e n.
(gemeint ist selbstredend die Kreislinie !)
Es gibt drei entsprechende c-Werte:
1.Fall
c = c1 = - 1 , ( d = d1 = 0 )
Die Hyperbel ist auf ihre Asymptoten a1,a2 reduziert ;
das Geradenpaar berührt den Kreis k in den Punkten
B1 ( 0 / 1) und B2 (1 / 0 ).
2:Fall
c = c2 = ½ + wurzel(2)
Berührungspunkt:
B3 ( - ½ * wurzel(2) / - ½ * wurzel(2) )
3.Fall
c = c3 = ½ - wurzel(2)
Berührungspunkt
B4 ( ½ * wurzel(2) / ½ * wurzel(2) )
Diese Resultate stimmen mit den von Fern präsentiereten überein .
Anmerkungn
1.) Man verifiziert leicht, dass die geforderte Berührung in allen
drei Fällen realisiert wird.
In den Fällen 2 und 3 stellt man sofort fest, dass die
Berührungspunkte aus Symmetriegründen mit den Scheitelpunkten
der Hyperbel übereinstimmen müssen und somit auf der Hauptachse
y = x liegen.
2.) Eine Erläuterung mit Beispielen zur Methode der
berührenden Niveaulinien findet man im Buch von Georg Polya
Mathematik und plausibles Schliessen, Birkhäuser Verlag, Basel
(Induction and Analogy in Mathematics, Princeton University Press)
3.) Würde mit f(x,y) = A* x ^ 2 + 2 * B * x * y + C * y ^ 2
eine quadratische Form vorgelegt, so liefern diejenigen Punkte
P1, P2, P3, .P4 auf dem Einheitskreis k die Extremalwerte von f(x,y)
auf k ,durch welche die Hauptachsen des Mittelpunktkegelschnittts
f(x,y) = const. gehen.
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
Fern

| | Veröffentlicht am Donnerstag, den 09. August, 2001 - 19:07: | 
|
Hallo Hans Rudolf,
Schön dass du wieder im Lande bist und, wie man sieht, in Superform, um hier die kniffeligen Aufgaben zu entwirren.
Hallo Bryan,
Wenn eine solche Funktion f(x,y) über einem Gebiet (z.B. Kreisfläche) untersucht werden soll, dann muss man
1) Extrempunkte von f(x,y) bestimmen,
2) Für diejenigen Punkte, die innerhalb des Gebietes liegen, feststellen ob es Max., Min. oder Sattelpunkte sind. (Hesse-Matrix).
3) Getrennt davon Extrempunkte und ihre Natur auf der Randkurve untersuchen (wie im obigen Beispiel).
4) Die Funktionswerte für alle Punkte (im Gebiet und am Rand) auflisten und so die globalen Max. und Min.-Werte bestimmen.
===========================================
Wäre in unserem Beispiel, die Kreisfläche gemeint, so würde sich nichts ändern, denn der einzige Extrempunkt (Sattelpunkt von f(x,y) liegt außerhalb des Kreises und braucht daher nicht berücksichtigt zu werden. Bei (1; 1).
===========================================
Gruß, Fern  |
    
Bryan (Bryan)

| | Veröffentlicht am Donnerstag, den 09. August, 2001 - 19:32: | 
|
Hallo Fern !
Ich denke jetzt habe ich es verstanden.
Vielen Dank für die ausführlichen Lösungen !
mfg
Bryan |
|