| Autor |
Beitrag |
    
Michael

| | Veröffentlicht am Dienstag, den 01. Mai, 2001 - 09:04: | 
|
Man beweise:Im Dreieck ist die vierfache Summe der Quadrate der Seitenhalbierenden gleich der dreifachen Summe der Quadrateder Seiten. |
    
badis

| | Veröffentlicht am Freitag, den 25. Mai, 2001 - 11:48: | 
|
wie mache ich, eine kreis anhand von drei punkt mit delphi |
    
Lerny

| | Veröffentlicht am Freitag, den 25. Mai, 2001 - 12:51: | 
|
Hi badis
kenne zwar nicht delphi, aber die Konstruktion von Hand geht so:
Nennen wir die drei Punkte A, B und C. Verbinde A mit B und B mit C und zeichne die Mittelsenkrechten zu den Strecken AB und BC. Der Schnittpunkt der Mittelsenkrechten ist der Kreismittelpunkt M.
mfg Lerny |
    
H.R.Moser,megmath.

| | Veröffentlicht am Freitag, den 25. Mai, 2001 - 15:40: | 
|
Hi Michael,
Beim Stöbern im Board bin ich auf Deine Aufgabe
vom 1.Mai gestossen.
Es dürfte an der Zeit sein, eine Lösung zu präsentieren.
Im Dreieck ABC mit den Seiten AB = c ,BC = a , CA = b
schneidet die Schwerlinie sa durch A die Seite BC in U.
Im Dreieck ABC gilt nach dem Kosinussatz
b^2 = a^2 + c^2 - 2 a * c * cos (beta), mithin
cos (beta) = [a^2+c^2 - b^2 ] / [ 2 * a * c ]
Dies setzen wir in die Formel
sa ^ 2 = c ^ 2 + ¼ * a ^ 2 - 2 * c * ½ a nach dem
Kosinussatz im Dreieck BAU ein und erhalten:
sa^2 = c^2 + ¼ * a^2 - ½ *(a^2 + c^2 - b^2), also
sa^2 = ½ * b^2 + ½ * c^2 - ¼ * a^2.
Durch zyklische Vertauschung erhält man für die anderen
Schwerlinien sb und sc:
sb^2 = ½ * c^2 + ½ * a^2 - ¼ * b^2
sc^2 = ½ * a^2 + ½ * b^2 - ¼ * c^2
Nun addieren wir die letzen drei Gleichungen und erhalten:
sa^2 + sb^2 +sc^2 = ¾ * [a^2 + b^2 + c^2], woraus die Behauptung sich unmittelbar ergibt.
Mit freundlichen Grüssen
H.R.Moser,megamath. |
    
Lemma5

| | Veröffentlicht am Freitag, den 25. Mai, 2001 - 18:39: | 
|
 |
    
Lemma5

| | Veröffentlicht am Freitag, den 25. Mai, 2001 - 18:41: | 
|
Hallo Megamath, es geht auch ohne Kosinussatz:
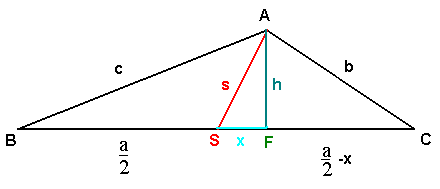
im oben skizzierten Dreieck ist S der Mittelpunkt der Seite BC mit |BC|=a.
Dann lässt sich auf die rechtwinkligen Dreiecke ABF und AFC der Satz des Pythagoras anwenden:
c²=h² + (x+ a/2)²
b²=h² + (x- a/2)²
auflösen der Klammern und addieren beider Gleichungen ergibt:
b²+c²=2h²+2x²+ax-ax+2a²/4
b²+c²=2h²+2x²+a²/2 (*)
und Pythagoras auf Dreieck FAS angewandt:
h²+x²=s², also auch 2h²+2x²=2s², ersetze dies in Gleichung (*):
b²+c²=2s²+a²/2 |-a²/2
b²+c²-a²/2 = 2s² |*2
4sa²=2b²+2c²-a² (a)
Dies galt für s als Seitenhalbierende sa der Seite a, entsprechende Gleichungen gelten für sb und sc:
4sb²=2c²+2a²-b² (b)
4sc²=2a²+2b²-c² (c)
addiere die Gleichungen (a), (b) und (c) =>
4(sa² + sb² + sc²)= 3(a²+b²+c²)
freundliche Grüße
Lemma5 |
    
Lemma5

| | Veröffentlicht am Freitag, den 25. Mai, 2001 - 18:52: | 
|
Hallo Megamath, ich habe dazu noch eine Frage, deren Beantwortung mir Probleme bereitet:
auf Klassen 8-10:Geometrie:Dreiecke:Beweis - Seitenhalbierende/Umfang wurde nach einem Beweis dafür gefragt, dass in jedem Dreieck die Summe der Längen der Seitenhalbierenden kleiner als der Umfang des Dreiecks ist.
Ist das hiermit gezeigt worden, oder könnte man das durch weitere Rechenschritte etwas deutlicher machen?
Reicht die von der Geometrie gegebene Einschränkung a,b,c,sa,sb,sc > 0 aus, dass man aus obigem schließen kann, dass gilt:
a+b+c>sa+sb+sc ? |
    
Lemma5

| | Veröffentlicht am Sonntag, den 10. Juni, 2001 - 20:35: | 
|
meine Frage oben hat sich erledigt. Die Vermutung stimmt nicht. Gegenbeispiel siehe hier |
|