| Autor |
Beitrag |
    
Karo

| | Veröffentlicht am Freitag, den 13. April, 2001 - 12:20: | 
|
Hallo, kann mir jemand mit folgender Aufgabe helfen?
f sein in jedem Intervall [0,x] integrierbar. Der Grenzwert g:= lim (t-> unendl.) f(t) möge existieren. Zeige, dass gilt:
lim(x->unendl.) 1/x Integr von 0 bis x f(t)dt = g. |
    
Fern

| | Veröffentlicht am Samstag, den 14. April, 2001 - 06:56: | 
|
Hallo Karo,
Nennen wir den gesuchten Grenzwert = A
Für x->oo wird das Integral auch +oo.
Wir haben es also mit dem Limes einer unbestimmten Form zu tun: oo/oo
Wir wenden die Regel von de l'Hospital an:
(ò0 xf(t)dt)' = [F(x)]' = f(x)
x' = 1
also: A=lim(f(x)/1) = lim(f(x)) für x->oo
Dieser Limes ist aber laut Vorgabe = g
Also A = g q.e.d.
================================= |
    
Karo

| | Veröffentlicht am Samstag, den 14. April, 2001 - 13:38: | 
|
Danke, aber was heißt q.e.d.? |
    
Fern

| | Veröffentlicht am Samstag, den 14. April, 2001 - 14:10: | 
|
quod erat demonstrandum |
    
sebi

| | Veröffentlicht am Samstag, den 14. April, 2001 - 17:31: | 
|
Warum ist de l'Hopital auf einen Ausdruck der Form ¥/¥ anwendbar? Ich dachte der gilt nur für 0/0 |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Samstag, den 14. April, 2001 - 20:39: | 
|
Hallo Karo
Ich habe den Beweis auch für nichtstetige Funktionen gefunden. Wenn Du Interesse hast, dann sag bescheid.
viele Grüße
SpockGeiger |
    
Karo

| | Veröffentlicht am Samstag, den 14. April, 2001 - 21:35: | 
|
Ja, kann ja nicht schaden! Wo hast Du ihn gefunden? |
    
OliverKnieps (Oliverk)

| | Veröffentlicht am Sonntag, den 15. April, 2001 - 00:10: | 
|
Hallo Fern,
Deinen Beweis finde ich sehr gut, allerdings stolpere ich über eine Stelle, und zwar deine Vorrausetzung, dass das Integral für x-> oo auch selbst gegen Unendlich strebt. Das ist nötig, um L'Hospital durchzuführen. Aber, z.B.: f(x) = e-x strebt für x -> oo gegen g = 0. Das Integral selbst, also F(x) = -e-x unter Beachtung der Grenzen x und 0 strebt aber dann für x -> oo
gegen 1. Das ist ein Durchbruch der Vorrausetzung. Wie schafft man Abhilfe? |
    
Fern

| | Veröffentlicht am Sonntag, den 15. April, 2001 - 07:39: | 
|
Hallo Oliver,
Du hast Recht: mein Beweis ist lückenhaft und gilt nur für g ¹0.
Der Fall g = 0 ist aber einfach zu zweigen:
ò0 oof(t)dt ist dann nicht oo sondern eine Konstante K.
und
g = lim(1/x*ò0 xf(t)dt) = lim(K/x) = 0 für x® oo.
===============
Schöne Ostergrüße,
Fern |
    
SpockGeiger

| | Veröffentlicht am Sonntag, den 15. April, 2001 - 12:35: | 
|
Hallo Karo
Das Wort "gefunden" hast Du falsch interpretiert, damit meinte ich eher, ich habe einen Beweis konstruiert. Hier ist er nun:
Mir fiel nichts besseres ein, als es elementar mit der e-Definition zu beweisen:
Die Voraussetzung f(x)->g besagt, dass für alle e>0 ein x0 existiert, sodass für alle x>x0 |f(x)-g|<e/2 gilt.
Die Integration ist monoton, also liefert die Integration beider Seiten:
òx0 x|f(t)-g|dt<òx0 xedt=e(x-x0)/2
Division durch x-x0 liefert:
òx0 x|f(t)-g|dt/(x-x0)<e/2
wobei man im Nenner auch Betragsstriche drummachen kann, da der Ausdruck positiv ist.
Nun weisen wir die Konvergenz mit der gleichen Definition nach:
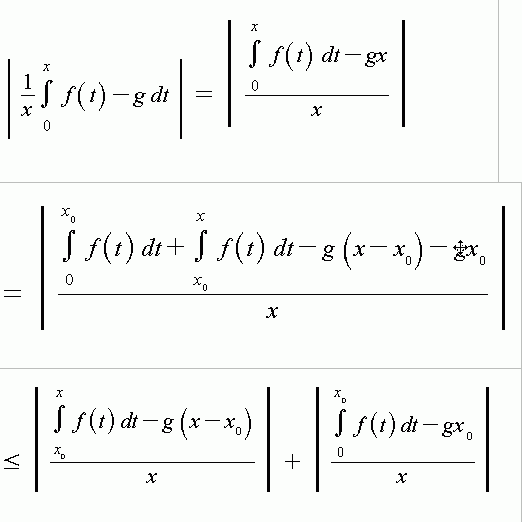

Im zweiten Summanden kommen im Zähler nur Konstanten vor, während das x im Nenner beliebig groß werden kann, daher gibt es ein x1, sodass für alle x>x1 der zweite Summand < e/2 ist. Daher ist der Gesamtausdruck für x>max(x0,x-{1}) kleiner als e/2+e/2=e, was zu beweisen war.
viele Grüße
SpockGeiger |
    
OliverKnieps (Oliverk)

| | Veröffentlicht am Sonntag, den 15. April, 2001 - 13:35: | 
|
Hallo SpockGeiger, hallo Karo,
der Beweis, dass L'Hospital auch bei Grenzwerten des Typs oo/oo Ergebnisse liefert, ist ebenso einfach wie kurz:
Sei f(x) = z(x)/n(x) und lim x -> oo z(x) = oo und lim x-> oo n(x) = oo. Unter Zuhilfenahme, dass also L'Hospital ursprünglich für x -> o bewiesen wurde, setzen wir x = 1/z und lassen dann z -> 0 laufen. Damit geht x gegen oo. Mit der Einführung der neuen Variablen z und der Operation z -> 0 können wir aber L' Hospital anwenden:
f(z) = z(1/z) / n(1/z)
also folglich
lim f(z) = [ (-1/z2) * z'(1/z) / (-1/z2) * n'(1/z) ] = [ z'(1/z) / n'(1/z)]
Bei Rücksubstituion ergibt das nun
lim f(x) = z'(x) / n'(x) wzbw!
x -> oo
Beste Grüße
 Oliver Oliver
z->0 |
    
h

| | Veröffentlicht am Samstag, den 21. April, 2001 - 13:08: | 
|
q |
|