| Autor |
Beitrag |
    
Mh (manfred)

Neues Mitglied
Benutzername: manfred
Nummer des Beitrags: 3
Registriert: 11-2001
| | Veröffentlicht am Montag, den 21. Oktober, 2002 - 18:52: | 
|
Hallo.
Gibt es eine Möglichkeit, ohne zu großes Hintergrundwissen den Beweis folgender Gleichung nachvollziehen zu können?
z(2k) = 22k-1 · p2k · |B2k| / (2k)!
(Ich interessiere mich für Bernoulli'sche Zahlen und kann mir in diesem Zusammenhang z.B. die Potenzreihenentwicklung der Tangensfunktion, aber auch die Potenzsummen-Formeln herleiten. Die obige Formel findet sich dauernd, ich habe jedoch keine Idee, wie man sie beweisen könnte.)
Danke für Eure Hinweise!
-----
| Mh |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 175
Registriert: 06-2001
| | Veröffentlicht am Montag, den 21. Oktober, 2002 - 20:50: | 
|
Hi Mh,
natürlich gibt es eine Möglichkeit:
Was Euler 1755 schafte sollte doch für uns ein Kinderspiel sein:-)
Frage an Mh:
wie sieht dein wissen in Funktionstheorie aus?
Als voraussetzung benötigen wir die Partialbruchentwicklung des Kotangens....
Wenn nicht vorhanden wird sie hergeleitet, ist kein problen, verlängert aber ein Wenig die Ausführungen!
mfg
Niels
|
    
tl198

Unregistrierter Gast
| | Veröffentlicht am Montag, den 21. Oktober, 2002 - 22:46: | 
|
Ich hätte interesse an der Herleitung!
Ein sehr interesantes Thema.
mfg
tl198 |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 176
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 22. Oktober, 2002 - 12:37: | 
|
zur Einstimmung ein paar Informationen über Bernoulli Zahlen:
Bernoulli Zahlen
Wenn noch eine Rückmeldung von Mh käme, wie es mit den Kotangens aussieht, dann könnte die "Sitzung" beginnen.
Gruß N. |
    
Mh (manfred)

Neues Mitglied
Benutzername: manfred
Nummer des Beitrags: 4
Registriert: 11-2001
| | Veröffentlicht am Sonntag, den 27. Oktober, 2002 - 10:26: | 
|
Mh meldet sich zurück. (Sorry, daß es etwas gedauert hat!)
Funktionentheorie interessiert mich sehr. Ich kann mein Wissen zwar nicht selber bewerten, denke aber, daß ich Dir folgen können werde.
Ähm, Cotangens-Partialbruchzerlegung habe ich nicht direkt parat, weiß aber, was damit gemeint ist. (Angabe reicht also, Herleitung soll Herausforderung für mich bleiben.)
Außerdem habe ich wiederum schon öfters gelesen, daß damit die gesuchte Herleitung möglich sein soll, also bin ich höchst gespannt...
Vielen Dank!
-----
| Mh |
    
Mh (manfred)

Neues Mitglied
Benutzername: manfred
Nummer des Beitrags: 5
Registriert: 11-2001
| | Veröffentlicht am Sonntag, den 27. Oktober, 2002 - 10:35: | 
|
Ich selber bin auch weitergekommen, und zwar mit der Fourierreihen-Entwicklung von geraden Potenzfunktionen, deren Koeffizienten ich sehr allgemein formulieren konnte.
Jetzt würde es genügen, zu zeigen, daß
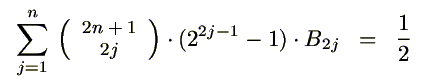
die Bernoulli'schen Zahlen definiert.
Meine Herleitung kann natürlich eingesehen werden:
-----
| Mh |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 182
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 27. Oktober, 2002 - 12:55: | 
|
Hi Mh,
vieleicht hilft dir dieser Denkanstoß:

(Quelle: Freitag - Busam Funktionstheorie 1 S 115)
Deine Herleitung ist nicht schlecht, basiert aber auf Fourrier - Reihen, die erst um 1820 entwickelt wurden.
Euler hatte einen anderen Beweis 1737 geführt.
Und dabei brauchte er die Partialbruchzerlegung des Kotangens.
Wir können jenen Beweis hier ja auch noch anführen-Wenn gewünscht.
viele Grüße
Niels
ps: Denke bei der Herleitung der Partialbruchzerlegung des Kotangens an den Residuenssatz!.
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 183
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 27. Oktober, 2002 - 13:01: | 
|
Hi Mh,
vieleicht hilft dir dieser Denkanstoß:

(Quelle: Freitag - Busam Funktionstheorie 1 S 115)
Deine Herleitung ist nicht schlecht, basiert aber auf Fourrier - Reihen, die erst um 1820 entwickelt wurden.
Euler hatte einen anderen Beweis 1737 geführt.
Und dabei brauchte er die Partialbruchzerlegung des Kotangens.
Wir können jenen Beweis hier ja auch noch anführen-Wenn gewünscht.
viele Grüße
Niels
ps: Denke bei der Herleitung der Partialbruchzerlegung des Kotangens an den Residuenssatz!.
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 184
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 27. Oktober, 2002 - 13:09: | 
|
Hi Mh,
vieleicht hilft dir dieser Denkanstoß:

(Quelle: Freitag - Busam Funktionstheorie 1 S 115)
Deine Herleitung ist nicht schlecht, basiert aber auf Fourrier - Reihen, die erst um 1820 entwickelt wurden.
Euler hatte einen anderen Beweis 1737 geführt.
Und dabei brauchte er die Partialbruchzerlegung des Kotangens.
Wir können jenen Beweis hier ja auch noch anführen-Wenn gewünscht.
viele Grüße
Niels
ps: Denke bei der Herleitung der Partialbruchzerlegung des Kotangens an den Residuenssatz!.
|
    
Mh (manfred)

Mitglied
Benutzername: manfred
Nummer des Beitrags: 27
Registriert: 11-2001
| | Veröffentlicht am Mittwoch, den 06. November, 2002 - 18:35: | 
|
Zuerst mal vielen Dank - auch für das Lob, obwohl der Beweis ja noch gar nicht fertig ist!
Die Definition der Bernoulli'schen Zahlen war mir bekannt; ich kann mir aus der Funktion über den hyperbolischen Cotangens (denn x/(ex-1) + x/2 = x/2 coth(x/2)) auch eine Reihe für den 'normalen' Cotangens herleiten, aber ich kann mir im Augenblick nicht denken, aus was ich Partialbrüche herleiten soll. (?)
Residuen sind mir schon ein Begriff, auch, daß es in diesem Zusammenhang einen Integralsatz gibt, aber ich fürchte, daß das schon an der Grenze meines funktionentheoretischen Wissens liegt.
Außerdem habe ich noch nicht verstanden, was das mit der Riemann'schen z-Funktion zu tun hat. (?)
Falls ich nicht lästig bin, bitte ich um weitere Erklärungen! Danke!
-----
| Mh |
    
Mh (manfred)

Mitglied
Benutzername: manfred
Nummer des Beitrags: 26
Registriert: 11-2001
| | Veröffentlicht am Dienstag, den 03. Dezember, 2002 - 17:40: | 
|
So, jetzt hab' ich's!
Endlich habe ich einen Artikel im Internet gefunden, dem ich eine Herleitung der Formel für die z-Funktion mit den Bernoulli'schen Zahlen entnehmen konnte.
Sie geht allerdings von der Produktdarstellung des Sinus' aus:
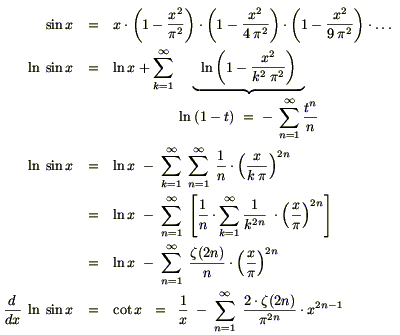
Vergleicht man die so erhaltene Reihe mit
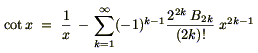 , ,
die man aus der Reihe für den Cotangens hyperbolicus herleiten kann, die sich wiederum schnell aus der Definition der Bernoulli'schen Zahlen ergibt, erhält man die bekannte Formel.
 mein ganzes Wissen über Bernoulli'sche Zahlen mein ganzes Wissen über Bernoulli'sche Zahlen
bernoulli.ps (76.3 k) |
In dem oben angesprochenen Artikel kommt die Partialbruchzerlegung des Cotangens schon in einer Alternative vor, diese kann ich leider nicht nachvollziehen.
Deshalb bin ich immer noch für weitere Beiträge dankbar!
-----
| Mh |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 231
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 08. Dezember, 2002 - 15:15: | 
|
Neuer Versuch:

Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 232
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 08. Dezember, 2002 - 15:32: | 
|
Teil II

Gruß N. |