| Autor |
Beitrag |
    
Lisette

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 04. Oktober, 2002 - 17:32: | 
|
Hallo,
Mit der folgenden Aufgabe komme ich nicht zurecht.
Wer kann mir helfen?
Man bestimme denjenigen Punkt auf der Exponentialkurve y = e^x,
für welchen die Kurvenkrümmung extremal ist.
Vielen Dank im Voraus.
Lisette
|
    
Muriel

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 04. Oktober, 2002 - 18:05: | 
|
Hallo Lisette,
einen solchen Punkt gibt es nicht! |
    
egal

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 04. Oktober, 2002 - 19:01: | 
|
Hi Lisette,
die Krümmung einer Kurve im Punkt (x | y(x)) ist definiert als
k = y" / (1 + (y')^2)^(3/2)
in deinem Fall
k = e^x / (1 + e^(2x))^(3/2)
Ableiten und Null setzen ergibt den Extremalpunkt
x = -ln(2)/2 , y = 1/√2
Der Krümmungskreis in diesem Punkt hat den minimalen Radius
r = 1/k = 3/2 * √3 ~ 2.598
|
    
megamath

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 04. Oktober, 2002 - 20:06: | 
|
Hi Lisette,
Gegeben ist die Funktion y (x) = e ^ x.
Wir erhalten die Krümmung k = kappa des Graphen mit der bekannten
Formel:
k = y ’ ’ / [1 + ( y’ ) ^ 2 ] ^ (3/2)
In unserem Fall entsteht:
k = k (x) = e ^ x / [1 + e ^ (2x) ] ^ (3/2)
Nun berechnen wir mit der Quotientenregel die erste Ableitung der Funktion k(x).
Es kommt:
k ’ (x) = { [1+e^(2x) ] ^ (3/2) * e^x – (3/2) * [1+e^(2x) ] ^ (1/2) * e^(2x) * 2 * e^x } /
{ [ 1+e^(2x)]^3}
Vereinfacht:
k ‘ (x) = (e^x) * { [1+e^(2x)]^1 – 3*e^(2x)} / { [ 1+e^(2x)]^(5/2)}
Setzt man k ‘ (x) gleich null,
so erhält man folgende Gleichung in x, deren Lösung den gesuchten x-Wert
für das gesuchte Extremum darstellt.
Die Gleichung lautet:
1 – 2*e^(2x) = 0
Daraus folgt:
x = - (1/2)*ln2
Der zugehörige y-Wert ist (1/2) * sqrt (2)
Dass die Krümmung maximal ist, ergibt sich aus der Anschauung.
Mit freundlichen Grüßen
H.R.Moser, megamath
|
    
Lisette

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 05. Oktober, 2002 - 05:16: | 
|
Hallo egal,
hallo megamath!
Vielen Dank für die Hilfe,
das ist ja sehr interessant!
Man würde die Stelle auf Anhieb woanders vermuten!
Lieben Dank an megamath für die ausführliche Herleitung!
Lisette |
    
Elsa13 (Elsa13)

Erfahrenes Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 148
Registriert: 12-2002
| | Veröffentlicht am Mittwoch, den 17. Mai, 2006 - 09:49: | 
|
Hi!
Mit der „Anschauung“ meinte megamath wohl, wenn man die Krümmungsfunktion betrachtet.
Denn an der Exponentialfunktion selbst kann man das nicht so einfach erkennen!
Weil ich diese Aufgabe interessant finde, hab ich in memoriam megamath eine Fleißaufgabe gemacht
und die 2. Ableitung an der Stelle x = - (1/2)*ln2 berechnet.
Natürlich ist sie – wie erwartet – negativ
und daher ist die Krümmung maximal.
Es ist

qed.
liebe Grüße
elsa |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 1810
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 17. Mai, 2006 - 13:09: | 
|
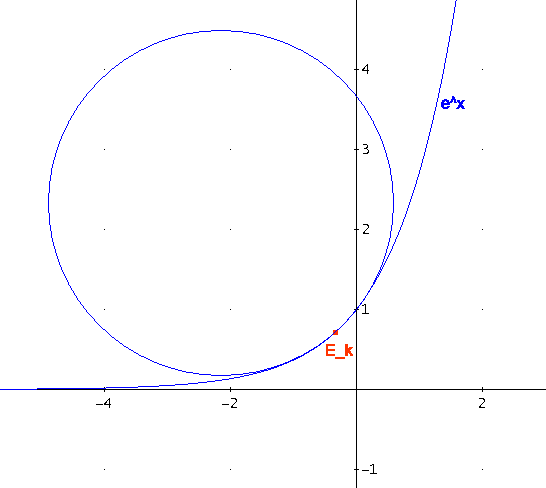
Wenn du den Graph der Kurve e^x betrachtest, siehst du, dass die Kurve sowohl bei größeren positiven, als auch negativen x-Werten immer flacher wird, d.h. dass dort die Krümmung kleiner wird. Im Bereich -2 bis +2 ist sie wesentlich größer, also ist darin ein Maximum zu erwarten. Insofern zeigt also bereits die Anschauung, dass es nur ein Maximum der Krümmung (d.h. einen minimalen Radius des Krümmungskreises) geben kann!
r = 1,5*sqrt(3)
Gr
mYthos
 |