| Autor |
Beitrag |
    
Sizilianer

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 18. September, 2002 - 13:40: | 
|
Hallo,
kann mir vielleicht jemand zeigen, wie man (egal, mit welchem Kon- bzw. Divergenzkriterium) beweisen kann, dass die Summe für n von 1 bis unendlich über:
ln(n)/n²
divergent ist?
|
    
egal

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 18. September, 2002 - 15:51: | 
|
Das wird niemand beweisen können, weil der negative Wert deiner Summe definitionsgemäß der Wert der Ableitung der Zetafunktion an der Stelle 2 ist. Allgemein ist
z'(s) = - S¥ n=1 ln(n)/n^s
für Re(s) > 1 definiert und endlich.
Durch einfache Integralabschätzung erhält man z'(2) < 1
|
    
egal

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 18. September, 2002 - 16:05: | 
|
... natürlich ist -z'(2)< 1 die interessantere Aussage ;-)
|
    
Sizilianer

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 18. September, 2002 - 21:21: | 
|
Danke für die Hilfe, aber verstanden habe ich kaum etwas. Wie kann z'(2) < 1 sein, und gleichzeitig ist die interessantere Aussage:
-z'(2) < 1 ?
Die Aufgabe stammt aus Kapitel 48 von
"Schaum's Outline: Differential- und Integralrechnung" von Frank Ayres
als eine von 16 Teilaufgaben unter dem Text, der im Original so heißt:
Untersuche mit dem Vergleichskriterium auf Konvergenz und Divergenz:
Summe(ln(n)/n^p)
und als Lösung ist angegeben: für p>2 konvergent
(aber kein Lösungsweg)
Bei den anderen 15 Aufgaben ist der Lösungsweg auch nicht nötig, weil die eigentlich so leicht sind, dass man sofort die korrekte Lösung findet, und die Zetafunktion braucht man erst recht nicht dafür, um sie zu lösen. Daher verwundert es etwas, wenn so eine schwere dazwischen ist. |
    
Ingo (ingo)

Moderator
Benutzername: ingo
Nummer des Beitrags: 512
Registriert: 08-1999
| | Veröffentlicht am Mittwoch, den 18. September, 2002 - 23:07: | 
|
Wie im Text gesagt geht es um das Integralvergleichskriterium.
Zu zeigen ist
ò1 ¥ ln(x)/xp konvergiert für p>2
partielle Integration liefert
[ ln(x)x-p+1/(1-p) ]1¥ - ò1 ¥ x-1x-p+1/(1-p)
=[ ln(x)x-p+1/(1-p) ]1¥ - (1/(1-p))ò1 ¥ x-p
= limx->¥ln(x)x-p+1/(1-p) - (1/(1-p))ò1 ¥ x-p
Das letzte Integral konvergiert für p>2 und der Grenzwert exisitert für p>1. Insgesamt ergibt sich die Konvergenz für p>2.
|
    
egal

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 19. September, 2002 - 07:57: | 
|
Hi Sizilianer,
1) Wenn du mir für einen Moment einfach glaubst, dass die Ableitung der Zetafunktion wie angegeben definiert ist, dann muss z'(s) < 0 gelten für alle s > 1 (die Summe von positiven Termen ist positiv, die Ableitung ist aber minus diese Summe). Daher ist z'(2) < 1 trivial (ich hab einfach vergessen das Minus hinzuschreiben), interessant ist -z'(2) weil das ja deine Summe ist!
2) Schaum's Outline gefällt mir sehr gut, bei der Lösung ist offenbar ein Druckfehler passiert, es muss heißen: "für p > 1 konvergent". Natürlich braucht man die Zetafunktion nicht zur Lösung dieser Aufgabe, ich hab das nur als Hinweis gemeint (und wollte mir Schreibarbeit ersparen, aber das rächt sich jetzt...). Wenn du nur die Konvergenz (ohne Abschätzung) zeigen willst ist die Aufgabe sicher nicht viel schwerer als die anderen: Verwende
(a) ln(n) wächst langsamer als jede Potenz n^e , e > 0
(b) S¥ n=1 1/n^p konvergiert für p > 1 (da sieht man jetzt den Zusammenhang mit der Zetafunktion z(p), aber man muss ihn nicht verwenden)
3) Für die Integralabschätzung interpretiert man deine Summe als Riemannsche Untersumme. Da muss man etwas aufpassen, da die Funktion f(x) = ln(x)/x^p , p > 1 , erst ab dem Hochpunkt bei x = e^(1/p) monoton fallend ist. Ab x = 3 funktioniert die Abschätzung für alle p > 1. Also
S¥ n=1 ln(n)/n^2 =
ln(2)/2^2 + ln(3)/3^2 + S¥ n=4 1/n^p <
ln(2)/2^2 + ln(3)/3^2 + ò3 ¥ ln(x)/x^2 =
ln(2)/2^2 + ln(3)/3^2 + (ln(3)+1)/3 ~ 0.9949 < 1
Das heißt also: -z'(2) < 1
Tatsächlich ist S¥ n=1 ln(n)/n^2 ~ 0.9375482543
Ingos Argument für p > 2 verstehe ich nicht, sein Integral konvergiert für p > 1.
|
    
Sizilianer

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 25. September, 2002 - 14:03: | 
|
Hi Ingo und egal,
Danke für die Hilfe.
Wenn es in Wirklichkeit heißen muss:
"für p > 1 konvergent",
dann ist die Aussage "für p>2 konvergent" ja nicht falsch, sondern nur unvollständig, oder?
Nur meine Behauptung dass die Reihe divergent ist, ist dann natürlich falsch.
zu 1) (von egal)
Das mit der Zetafunktion habe ich nachgesehen und ich glaube jetzt, dass die Ableitung der Zetafunktion wie angegeben definiert ist. Ich möchte noch um Entschuldigung bitten, dass ich mich etwas dumm angestellt habe bei meiner Nachfrage wegen -z'(2) < 1.
Aber der Vollständigkeit wegen noch eine Frage:
Ist die Aussage "z'(s) < 0 für alle s > 1" vielleicht noch auf weitere Werte von s ausdehnbar?
Gilt z'(s) < 0 vielleicht sogar für alle s € lR ?
Also nicht bloß für s>1 ?
zu 2)
Die beiden Aussagen, die ich zum Beweis 2) verwenden soll,
muss ich erst noch beweisen.
(a) ln(n) wächst langsamer als jede Potenz n^e , e > 0
Ich weiß bisher nur, dass (ln(n))^p / n für beliebiges p eine Nullfolge ist. (Beweis hier)
Benutze ich nun, dass dann auch die Folge ln(n)/n gegen 0 geht, weiß ich, dass
ln(n)/n^e für alle e >= 1 gegen 0 konvergiert.
Aber der Fall 0 < e < 1 bleibt für mich noch offen.
(b) Soo n=1 1/n^p konvergiert für p > 1
Der Beweisablauf ist zwar im Bronstein angegeben, aber ich verstehe ihn nicht.
zu 3) und zu Ingos Antwort:
In euren Antworten habt ihr beide Gebrauch vom Integralvergleichskriterium gemacht.
Gerade das Kriterium wollte ich aber nicht benutzen, weil bis zu dem Punkt der Vorlesung noch gar keine Integrale definiert waren.
Ich ging sowieso davon aus, dass ich das Integralvergleichskriterium nicht benutzen muss, denn in dem Buch von Ayres, das ich habe, steht:
II. DAS INTEGRALKRITERIUM
Das allgemeine Glied in der Reihe Ssn sei durch f(n) gegeben.
Gilt f(x)>0 und ist f(x) im Intervall x>x nichtwachsend, wobei x eine natürliche Zahl ist, dann konvergiert (divergiert) Ssn, je nachdem, ob òx+oo f(x) dx existiert oder nicht.
III. DAS VERGLEICHSKRITERIUM FÜR KONVERGENZ
Eine positive Reihe Ssn konvergiert, wenn jedes Glied (unter Umständen erst nach endlich vielen) kleiner oder gleich dem entsprechenden Glied einer bekannten konvergenten Reihe Scn ist.
IV. DAS VERGLEICHSKRITERIUM FÜR DIVERGENZ
Eine positive Reihe Ssn divergiert, wenn jedes Glied (unter Umständen erst nach endlich vielen) größer oder gleich dem entsprechenden Glied einer bekannten divergenten positiven Reihe Sdn ist.
Vielleicht habt ihr nicht die gleiche Auflage wie ich.
Ich denke, mit den beiden Vergleichskriterien III und IV zusammen ist so etwas gemeint wie das Majorantenkriterium, d.h. bei III. muss man eine bekannte konvergente Majorante suchen und bei IV. muss die zu untersuchende Reihe eine Majorante einer bekannten divergenten Reihe sein.
Also auf jeden Fall ohne dies Integralkriterium.
Ich denke aber, dass ich notfalls auch ohne diese Aufgabe zu verstehen weiterleben kann. ;-)
|
    
egal

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 25. September, 2002 - 15:36: | 
|
Hallo Sizilianer,
freut mich, dass du meine Antwort so genau durchgearbeitet hast.
zu 1): z'(s) < 0 gilt schon für weitere Werte von s, aber nicht für alle rellen s. Man erkennt das anschaulich in folgendem Diagramm der Zetafunktion (links eine Vergrößerung für s < 0). z'(s) < 0 bedeutet ja fallender Graph:

zu 2a): Berechne lim(n->oo) ln(n)/n^e , e > 0, mit l'Hospital.
Du hast sicher bemerkt, dass ich bei 3) gleich bei der ersten Umformung (bei Summe n=4 bis oo) den falschen Summanden kopiert habe: statt 1/n^p gehört natürlich ln(n)/n^2.
Wie erwähnt braucht man das Integralkriterium nicht, wenn nur die Konvergenz (ohne Abschätzung) gezeigt werden soll. Vielleicht war die abgeschwächte Aussage "für p>2 konvergent" wirklich nur als Vereinfachung gedacht, wo man den Beweis "mit freiem Auge" sieht (und deshalb im Buch keiner angegeben ist).
|
    
egal

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 25. September, 2002 - 15:40: | 
|
das mit den Bildern ist so ein Problem...

|
    
egal

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 26. September, 2002 - 08:11: | 
|
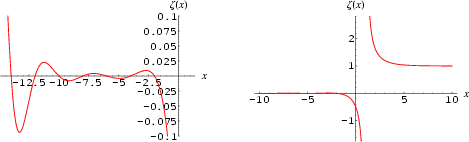
|
    
Sizilianer

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 26. September, 2002 - 20:58: | 
|
Hi egal,
zu meiner Vermutung "Gilt z'(s) < 0 vielleicht sogar für alle s € lR ?"
Ich versuche, sie zu belegen:
z'(s) = -Soo n=1 ln(n)/n^s
Vermutung: Soo n=1 ln(n)/n^s > 0 für alle s € lR.
Begründung:
für n=1 ist ln(n)/n^s = 0, für n>1 gilt:
ln(n) ist positiv und n^s ist positive für alle s € lR.
Summiert werden alle Quotienten aus ln(n) und n^s, und da diese nie negativ sind, kann auch die Summe Soo n=1 ln(n)/n^s nie negativ sein.
Hieraus schließe ich, dass
z'(s) = -Soo n=1 ln(n)/n^s < 0 für alle s € lR
Aber ich kann den Fehler nicht finden, warum das falsch ist.
zu 2)
für (a) ln(n) wächst langsamer als jede Potenz n^e, e > 0
stelle ich mir einen Beweis ungefähr so vor:
hier wurde bewiesen, dass (ln x)p/x -> 0 für x --> unendlich geht.
Kann man dann nicht einfach die p-te Wurzel ziehen
und behaupten:
für x --> unendlich geht ((ln x)p/x)^(1/p) -> 0 , also
(ln x)/x^(1/p) --> 0
und dann 1/p = e setzen?
Dann stünde da:
(ln x)/x^e --> 0
Ließe sich so nicht beweisen, dass ln(n) langsamer wächst als jede Potenz n^e, e > 0 ?
Ein Problem damit ist noch, dass p nur ein natürliche Zahl sein kann, dass also e nicht alle Zahlen mit 0<e<1 durchläuft.
Ich möchte gerne ohne l'Hospital rechnen, da ich keine Ableitungen verwenden will.
Ich denke, das war ironisch gemeint, dass ich deine Antwort "so genau durchgearbeitet" hätte, denn das habe ich bis heute noch gar nicht.
Ich habe den letzten Teil vom 19. Sept. hinter 3) durchgerechnet und frage mich nun noch, woher diese Aussage kommt:
Tatsächlich ist Soo n=1 ln(n)/n^2 ~ 0.9375482543
|
    
egal

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 27. September, 2002 - 08:42: | 
|
1) Dein Fehler liegt darin, dass die verwendete Summe für s<1 divergiert! Diese Reihendarstellung von z(s) bzw. z'(s) gilt nur für Re(s)>1.
2) Ja, du kannst mit der p-ten Wurzel argumentieren und die nicht ganzzahligen 1/e durch das nächstgrößere p abschätzen.
3) z'(2) ~ -0.9375482543 findest du in Tabellen zur Zetafunktion oder z.B. mit Maple. Es gibt meines Wissens keine "schöne Formel" (wie z(2) = p²/6) dafür.
|
    
Sizilianer

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 10. Oktober, 2002 - 18:44: | 
|
Hi egal,
endlich bin ich wieder dazu gekommen, die restlichen Unklarheiten anzugehen.
bei 1)
bin ich mir inzwischen vollkommen unsicher.
Ich habe dazu eine ausführlichere Frage auf http://www.mathehotline.de/mathe4u/hausaufgaben/messages/9308 /128810.html gestellt.
zu 2)
Ist diese Argumentation hieb- und stichfest?
Zu zeigen ist die Gültigkeit der Behauptung:
ln(n) wächst langsamer als jede Potenz n^e , e > 0
Beweis in zwei Bereichen für e:
1) e >= 1
2) 0 < e < 1
Dabei wird benutzt, dass
(3) (ln x)^p /x gegen 0 geht, wenn x immer größer wird. (Beweis hier), insbesondere folgt damit für p=1:
(3) => ln(x)/x --> 0 für x --> oo
und damit ergibt sich für
Bereich 1) e >= 1:
ln(x)/x^e ---> 0 für x ---> oo
Bereich 2) 0 < e < 1:
gehe wieder aus von der Gültigkeit von (3) (ln x)^p /x ---> 0
ln(x)/x^e = ( (ln(x))^(1/e) / x )^e
Für (hinreichend) große Werte von x gilt wegen 1/e > 1:
(ln(x))^1/e < (ln(x))^(c + 1/e) mit 0 <= c < 1.
c lässt sich immer so wählen, dass c + 1/e eine natürliche Zahl ist, wobei natürlich c + 1/e >= 1/e gilt.
also lässt sich p:= c+1/e setzen und damit lässt sich wieder (3) anwenden:
(ln x)^p /x geht für größer werdende x gegen 0,
also geht auch die p-te Wurzel daraus:
ln(x)/x^(1/p) gegen 0, wobei 1/p = 1/(c+1/e) = e/(c/e + 1) ist.
Damit geht auch (ln(x))^1/e gegen 0, wenn x gegen unendlich geht.
Ich danke dir, dass du dich hiermit beschäftigt hast. |
|