| Autor |
Beitrag |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Sonntag, den 04. Februar, 2001 - 09:09: | 
|
Hallo,
Ich suche zu folgender Behauptung einen Beweis:
Für jedes beliebige positive reelle t gilt

Die Schwierigkeit besteht darin, für die bestimmten Integrale äquivalente Ausdrücke zu finden. Doch bisher kenne ich leider kein Mittel, sie in eine andere Form umzuwandeln.
Kay |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Sonntag, den 04. Februar, 2001 - 09:21: | 
|
C:\WINDOWS\DESKTOP\Kay\Mathe
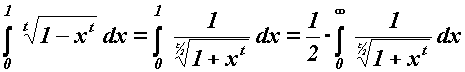 image1.gif image1.gif |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Sonntag, den 04. Februar, 2001 - 09:25: | 
|
Sorry, der Image-Upload funktionierte nicht ganz richtig.
Kay |
    
Stefan (Stefan26)

| | Veröffentlicht am Freitag, den 09. Februar, 2001 - 13:50: | 
|
Hallo Kay,
ich habe versucht es zu beweisen, ist aber vermutlich nicht so einfach. Jedes Integral ist für t>2 nicht elementar und läßt sich nur mittels Hypergeometrischer Funktionen ausdrücken.
Für t=2 kann man die Integrale aber ausrechnen und erhält für die beiden ersten Pi/4.
Allerdings ist das letzte Integral so nicht richtig, denn es kommt 1/2 - Pi/2.
Wo hast Du diese Identitäten her? Wie lautet das rechte Integral richtig?
Im Fall t=2 kann man durch partielle Integration zu ähnlichen Integralen gelangen -- dies beantwortet Deine Frage nach einem Mittel bestimmte Integrale in eine andere Form umzuwandeln: partielle Integration und Substitution. Leider ist es mir damit nichteinmal für t=2 gelungen die Gleichheit zu beweisen. |
    
Kay Schönberger (Kay_S)

| | Veröffentlicht am Samstag, den 10. Februar, 2001 - 10:05: | 
|
Danke erst einmal für die Antwort!
Auf die Identitäten bin ich nur "zufällig" gestoßen. Das rechte Integral ist schon richtig - es ist ein Produkt (das Minuszeichen ist keins - wohl mein Fehler).
Was mich interessieren würde sind die "hypergeometrischen Funktionen".
Gibt es dazu Literatur oder Artikel im Internet?
Kay |
    
Stefan (Stefan26)

| | Veröffentlicht am Sonntag, den 25. Februar, 2001 - 00:06: | 
|
Die klassiche hypergeometrische Funktion F(a,b,c;z) wurde von Gauß eingeführt und ist durch folgende Reihe definiert:
F(a,b,c;z) = Sum[k=0,oo] (a)k(b)k / (c)k . zk / k! = Sum[k=0,oo] (a)k(b)k / [(c)k(1)k] zk
wobei (a)k := a(a+1)...(a+k-1) das Pochhammersymbol ist.
Sie ist EINE Lösung y(z) der Differentialgleichung
z(1-z)y'' + [c-(a+b+1)z]y' - aby = 0.
Betrachte den einfachen Spezialfall F(1,b,b;z) = Sum[k=0,oo] zk = 1/(1-z).
Bücher über die Hypergeometrische Funktion gibt es viele, die Materie ist aber ordentlich kompliziert. Für den Anfang reicht ein Buch über spezielle Funktionen. Guck mal in der Bibliothek.
Auf jeden Fall ist die Hypergeometrische Funktion sehr schön und interessant.
Für Dein unbestimmtes Integral gilt:
(*) Int (1-xt)1/t dx = x F(1/t, -1/t, 1+1/t; xt). Versuche den Beweis selbst, benutze die allgemeine Binomische Reihe
(1+x)a = Sum[k=0,oo] (a,k) zk
wobei (a,k) := a(a-1)...(a-k+1) / k! der allgemeine Binomialkoeffizient ist. Setze nun für x : -xt und t : 1/t ein und integriere die Reihe gliedweise. Nach Umformung der Koeffizienten hast Du dann (*) bewiesen.
Für das andere Unbestimmte Integral gilt:
(**) Int (1+xt)-2/t dx = x F(1/t, 2/t, 1+1/t; -xt). Was Du genauso beweist.
Da an der unteren Grenze x=0 beide Integrale verschwinden, ist also nur noch zu beweisen:
F(1/t, -1/t, 1+1/t; 1) = F(1/t, 2/t, 1+1/t; -1)
Doch dazu später. Versuche ersteinmal mir bis dahin zu folgen. Wenn etwas unklar oder Du mit den Rechnungen nicht klarkommst frage bitte nach.
Stefan |
|