| Autor |
Beitrag |
    
Marcel

| | Veröffentlicht am Sonntag, den 07. Januar, 2001 - 20:03: | 
|
Hallo Leute.
Kann mir jemand bei dieser Mathehausaufgabe
helfen. Wäre echt nett von euch.
Ich danke euch im voraus.
Mfg Marcel
Aufgabe:
Aus einer Kugel mit dem Radius R wird durch zwei
parallel zueinander ausgeführte Schnitte im Abstand a bzw. a+d vom Mittelpunkt eine Scheibe der Dicke d ausgeschnitten.
Berechnen Sie das Volumen einer solchen Scheibe.
a)für R=6,a=2,d=1.
b)für R=6,a=3,d=1
c)allgemein für beliebige R,a und d.
Außerdem gegeben: F(x)=R^2-x^2 und davon die Wurzel!!
Viele, vielen Dank!!!!!!!!!!!! |
    
Matroid (Matroid)

| | Veröffentlicht am Sonntag, den 07. Januar, 2001 - 20:22: | 
|
Hi Marcel,
die letzte Gleichung F(x) ist ein Kreis mit Radius R um den Nullpunkt des Koordinatensystems. Wenn man diese Funktion um die x-Achse rotieren läßt, dann entsteht eine Kugel. Für das Volumen des Rotationskörpers einer Funktion um eine Achse gibt es eine bekannte Formel 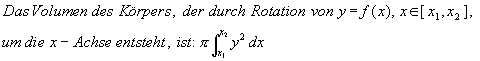
Die Grenzen der Rotation sind durch a und a+d gegeben.
Dann mußt Du noch ein Integral lösen und die Grenzen einsetzen.
Gruß
Matroid |
    
H.R.Moser,megamath.

| | Veröffentlicht am Montag, den 08. Januar, 2001 - 12:00: | 
|
Hi Marcel,
Die Formel für das Volumen der Kugelzone oder
Kugelschicht soll nun noch ausführlich hergeleitet
werden
Bezeichnungen:
p und q seien die beiden Randkreisradien
( Radien der Grund -und Deckfläche ),
d sei die Höhe der Schicht.
Für das Volumen V leiten wir eine Formel her,
in welcher der Kugelradius R nicht explizit auftritt
Diese Formel lautet.:
V = Pi* d / 6 * ( 3 p ^ 2 + 3 q ^ 2 + d ^ 2 )
Herleitung mit Integralrechnung
Die Kugel entsteht durch Rotation der Kreises x^2 + y^2 = R^2
um die x-Achse.
Die Ebenen der Randkreise haben wie in der Aufgabenstellung
verlangt, die Abstände a und a+ d vom Kugelmittelpunkt O.
V ergibt sich als Integral:
V= int [Pi*(R^2 - x^2) * dx ],untere Grenze a, obere Grenze a + d.
Eine Auswertung mittels der Stammfunktion R^2 x - x^3 / 3 führt auf:
V = Pi * { R^2 * ( a + d ) - 1/3 *(a+d)^3 -R^2 * a + 1/3 * a^3 }
Wir lösen Klammern und fassen neu zusammen:
V = Pi * { R^2 * d - 1 / 3 * ( 3 a ^ 2 * d + 3 * a* d ^2 + d ^3 ) } =
Pi / 3 * { 3*R^2 * d - 3 * a^2 * d - 3 * a * d^2 - d ^ 3 }.............(1)
Auch: V = Pi * d / 6 * [ 6 * R^2 - 6 * a^2 - 6 * a * d - 2 * d^2 ]
Nun führen wir die Randkreisradien p und q ein und ersetzen
den Term T in der eckigen Klammer.
Mit p^2 = R^2 - a^2 und
q^2 = R^2 - ( a + d ) ^2 = R^2 -a^2 - 2 a d - d^2
gewinnen wir den Ausdruck
3 p ^ 2 + 3 q ^ 2 + d ^2 gerade den gesuchten Term T, wie man leicht nachrechnet.
Somit gilt:
V = Pi * d / 6 * [3 * p^2 + 3* q^2 + d^2 ] ............................................(")
Bemerkungen
1)Um Deine numerischen Beispiele auszuwerten, kannst Du die
Formel (1) benützen.
2) Man kann die Volumenformel auch ohne Integralrechnung
herleiten, indem man V als Differenz zweier Kalottenvolumina
darstellt.
(siehe die entsprechende Herleitung ohne Integralrechnung in
meiner Antort an Tommi vom 7.1.2001,Stichwort "Kugelkappe").
3.)Führt man den Radius m des Mittelschnittes der Kugelschicht ein
(Parallelschnitt zur Grundfläche in halber Höhe d/2),
so erhält man eine von Colin Maclaurin (1698-1746) hergeleitete Formel:
V = Pi * m ^ 2 * d - Pi * d ^ 3 / 12.
4) Für die Radien p , q , m und die Höhe d gilt die Relation
4 m ^2 = 2 p^2 + 2 q^2 + d^2.
5) Wir können leicht bestätigen, dass für das Volumen der Kugelschicht
die Simpsonsche Regel gilt:
V = 1/6* d * (G + 4*M + D) mit
G: Grundläche, M : Fläche des Mittelschnittes, D: Deckfläche.
Mit freundlichen Grüssen
H.R.Moser,megamath. |
|





