| Autor |
Beitrag |
    
raff_nix

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 11. Juni, 2002 - 01:11: | 
|
Hallo allerseits,
wie loest man eine Gleichung die folgendermassen aussieht:
3*sin(x-pi)=2 betrachtet im Intervall 0<x<2pi
bitte um schnelle Hilfe |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 11. Juni, 2002 - 15:54: | 
|
Hallo raff_nix,
3*sin(x-pi)=2
<->
sin(x-pi)=2/3
Nun ist
sin(pi-a)=sin(a) (*)
und sin(-b)=-sin(b) (**)
=>
sin(x-pi)=2/3
<->
sin(-(pi-x))=2/3
=> mit (**)
-sin(pi-x)=2/3
<->
sin(pi-x)=-2/3
=> mit (*)
sin(x)=(-2/3)
=>
y=arcsin(-2/3)=-0,7297 (beim TR (Taschenrechner) auf RAD umstellen!!!)
Nun benötigen wir aber x so, dass 0<x<2pi gilt. Es ist y<0! Wir wissen aber:
sin(g+2pi)=sin(g), also ist
0<x1=y+2pi=5,5535<2pi
Ausserdem ist sin(2pi+y)=sin(pi-y)
Also ist eine weitere Lösung:
0<x2=pi-y=3,8713<2pi
Kontrolle:
3*sin(x1-pi)=3*sin(5,5535-pi)=1,9999(ungefähr 2)!
3*sin(x2-pi)=3*sin(3,8713-pi)=1,9999(ungefähr 2)!
Beachte übrigens:
Du mußt den Taschenrechner auf RAD umstellen. Drückst du 90 und dann sin und du erhältst 1, so steht er auf DEG. Gibst du pi/2 ein und dann sin und du erhältst 1, so steht er richtig (auf RAD)!
Mit freundlichen Grüssen
M. |
    
raff_nix

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 13. Juni, 2002 - 22:24: | 
|
Hallo M.
ich danke Dir mehrmals, das war hilfreich. Für sowas bin ich einfach zu doof, das kann ich mir nicht vorstellen.
Tausend Dank
|
    
M.

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 13. Juni, 2002 - 23:40: | 
|
Hallo raff_nix,
vorstellen kann ich es mir schon (kennst du die Sinus-/Kosinus"Definition" am Einheitskreis?), aber was viel wichtiger ist, es ist beweisbar (die verwandten Hilfssätze sind gemeint!). Doch dies würde über das Schulniveau etwas!!! hinausgehen. Man kann zeigen, dass sich eine komplexe Zahl als unendliche Reihe darstellen läßt. Diese kann man als Definition der exp-Funktion benutzen. Nun zeigt man, dass exp(1)=e und das e^z=exp(z) ist (beachte: exp ist die unendliche Reihe). Dann zeigt man:
|e^ix|=1 (i ist die komplexe Zahl (0,1) mit i^2=-1) für alle x aus IR. Irgendwie müßte sich jetzt auch noch zeigen lassen, dass e^(ix) im Intervall [0,2pi] surjektiv ist (dass heißt, für jeden Wert y im Intervall [0, 2pi] gibt es ein ein reelles x so, dass e^(ix)=y). Momentan weiß ich nicht unbedingt, wie das geht. Logarithmuß kann man meiner Meinung nach nicht benutzen, weil er eben dies schon voraussetzt. Vielleicht hat jemand eine Idee (bitte keine geometrische! also bitte nicht über Gaußebene!).
Nun definiert man sin(x)=Imaginärteil(e^(ix)) und cos(x)=Realteil(e^(ix)). Damit ergeben sich einige wunderbare Eigenschaften dieser Funktionen. Und da e^(ix)=exp(ix) läßt sich der Sinus und der Cos auch wunderbar als unendliche Reihe schreiben. Aber in der Schule fehlen einem dazu einige (elementare) Grundlagen bzw. werden nicht sorgfältig genug behandelt(was ja auch nicht immer möglich ist, allein wegen des "Zeitdruckes"!)
Mit freundlichen Grüssen
M. |
    
Niels (niels2)

Mitglied
Benutzername: niels2
Nummer des Beitrags: 45
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 14. Juni, 2002 - 09:55: | 
|
Hi M,
von welchen Hilfssätzen sprichst du?
Gruß N. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 14. Juni, 2002 - 12:04: | 
|
Hallo Nils,
i) sin(pi-x)=sin(x)
ii) sin(2pi-x)=-sin(x)=sin(-x)
und ähnliches. Ebenso die Additionstheoreme. Man sollte immer bedenken, dass eine geometrische Definition des Sinus immer Tücken und Lücken läßt! Die geometrische Interpretation ist meiner Ansicht nach immer eine Plausibilitätsbegründung, aber kein Beweis. Vielleicht ist so etwas aber auch Ansichtssache!
Das Problem bei einer Definition über das Bogenstück (am Einheitskreis) besteht meiner Ansicht nach daraus, dass eine Defintion über das Bogenstück nicht besonders "schön" für die Defintion einer Funktion ist. Wie will man das Bogenstück exakt angeben? Im Prinzip gibt es bei einer solchen Definition einige exakte Werte (vielleicht für pi/2, pi/6 etc., wobei die schulische Definition von pi doch etwas fragwürdig ist), es gibt aber unendlich viele Werte, wo es uns unmöglich bleibt, den genauen Sinuswert zu berechnen. Wir müßten also versuchen, uns eine solche Funktion hinzuschreiben. Dabei gelangen wir aber zu Schwierigkeiten, gerade wegen der "Ungenauigkeit" bei unendlich vielen Werten (wie genau ist eine geometrische Übertragung des Sinus?). Solche Probleme treten bei der obigen "Definition" nicht auf.
Mit freundlichen Grüssen
M. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 14. Juni, 2002 - 12:22: | 
|
PS:
-Irgendwie müßte sich jetzt auch noch zeigen lassen, dass e^(ix) im Intervall [0,2pi] surjektiv ist (dass heißt, für jeden Wert y im Intervall [0, 2pi] gibt es ein ein reelles x so, dass e^(ix)=y)-
Mir ist gerade aufgefallen, dass dieser Satz falsch ist und ich eigentlich etwas anderes meine:
Man müßte zeigen, dass für jedes komplexe z mit |z|=1 eine Darstellung der Form e^(ix)=z exisitiert, wobei x aus [0,2pi] gilt.
Mit freundlichen Grüssen
M. |
    
Niels (niels2)

Mitglied
Benutzername: niels2
Nummer des Beitrags: 49
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 14. Juni, 2002 - 17:24: | 
|
Hi M,
da habe ich aber konträre Ansichten:
Geometrische Beweise sind grundsätzlich genauso gültig, wie analytische Beweise oder Definitionen.
Ob nun der Sinus als unendliche Reihe oder als Länge eines Bogenstücks definiert ist spielt meiner Meinung nach keine Rolle. Beide Definitionen sind zwar in der Theorie richtig, aber für die praktische Anwendung manchmal nur bis zu einer bestimmten Genauigkeit brauchbar.
Natürlich kannst du nicht jeden Sinuswert genau am Einheitskreis exakt konstruieren, du kannst aber ebensowenig jeden Sinuswert genaue berechnen, weil es nicht möglich ist unendlich viele Summanden aufzuaddieren. Das gilt übrigens auch für die Exponentialreihe!
Der große Vorteil solcher geometrischen Beweise ist-Wie du selbst sagst-die Plausabilität des Beweises oder der Definitionen.
Bei Pi ist das ähnlich:
Ob man pi als Proportionalitätskonstante von Umfang und Durchmesser am Kreis definiert oder als Arcustangensreihe ist doch volkommen gleich; beides ist möglich. Natürlich kann man argumentieren, dass die Arcustangensreihe viel genauer Berechnung von Pi zu lässt. Aber ob es so sinnvoll für den täglichen praxisgebrauch auf über eine Million stellen zu berechnen wage ich zu bezweifeln. So ist es mit den Sinuswerten!
zu i)
Das liegt an der punktsymetrie der Sinusfunktion zum Ursprung. Das kann man auch am Einheitskreis zeichnen.
ii)Ebenfals Symetrie und Periodizität sind die Gründe für die Beziehungen!
Gruß N. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 14. Juni, 2002 - 18:09: | 
|
Hallo N.,
ich bezweifle gar nicht, dass die Beweise in der Geometrie richtig sind. (Ich beweise selber auch viel geometrisch).Nur finde ich Beweise, die analytisch geführt werden, einfach logischer, eindeutiger und nachvollziehbarer.
Zu i),ii)
Das kann man natürlich über Symmetrie und kongruente Dreiecke herleiten, keine Frage. Mache ich selber meistens so, wenn ich es einem Nachhilfeschüler erkläre!
Nur während der Beweis des Satzes:
sin(x+y)=sin(x)cos(y)+sin(y)cos(x) geometrisch sehr aufwendig ist, ist er mit der Definition des Sinus als Imaginärteil(e^(ix)) sehr elegant.
e^(i(x+y))=cos(x+y)+i*sin(x+y)=e^(i(x+y))=e^(ix)*e^(iy)=[cos(x)cos(y)-sin(x)sin(y)]+i[sin(x)cos(y)+sin(y)cos(x)]
(vergleiche die Imaginärteile!)
Vielleicht hatte ich mich etwas falsch ausgedrückt:
Man kann aus den Gesetzen für Grenzwerte einige Beziehungen für sin, cos beweisen. Dabei braucht man ´im wesentlichen´ nur Rechengesetze. In der Geometrie braucht man doch noch ein paar Hilfssätze über kongruente Dreiecke etc.
Versteh mich nicht falsch. Ich möchte hier auf gar keinen Fall die Geometrie in Frage stellen, nur für mich persönlich finde ich analytische Beweise einfach logischer und nachvollziehbarer. Natürlich kann man auch die Richtigkeit der analytischen Theorie in Frage stellen. Das ist Ansichtssache.
Ich finde eine Verknüpfung beider Theorien (analytische und geometrische) auch gar nicht so verkehrt! Geschieht ja teilweise sogar auch in der Analysis!
Mit freundlichen Grüssen
M. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 14. Juni, 2002 - 18:36: | 
|
Na okay, ich hatte das doch in meinem ersten Text anders geschrieben als gemeint:
...Interpretation ist meiner Ansicht nach immer eine Plausibilitätsbegründung, aber kein Beweis...
Es ist schon ein Beweis, aber ich zweifle eher an solchen Beweisen wie an analytischen.
Na, belassen wir es dabei. Ansichtssache?!
Mit freundlichen Grüssen
M.
|
    
Niels (niels2)

Mitglied
Benutzername: niels2
Nummer des Beitrags: 50
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 14. Juni, 2002 - 19:05: | 
|
Hi M,
das hört sich wieder so an als ob die Analysis ohne Hilfsätze auskäme...
Was in der Analysis die Hilfssätze das sind in der Geometrie halt die Hilfskonstruktionen!
Ich gebe ja zu das es meist einfacher ist irgentwelche Analytischen Beweise zu führen, frei nach dem Motto:
Aus Lemma A und Hilfssatz B folgt unter Anwendung des Corrolar C Satz D
Das "Zusammensätzen" solcher Teile zu einem Beweis ist halt scheinbar einfacher als sich hochkomplizierte Hilfskonstruktionen zu überlegen.
Dennoch haben solche Beweise auch ihren Scarm...
Mir sind für Additionstheoreme alleine mindestens 3 rein geometrische und z.t analytische Beweise bekannt.
Wenn man die geometrische konstruktione kennt und gut erklären kann können solche Sätze auch sehr elegant hergeleitet werden.
Ich habe hier im Board auch schon x mal die Additionstheoreme hergeleitet.
Schau sie dir an!
Ich bin aber immer etwas skeptisch wenn man große Geschütze wie die Komplexen Zahlen für sowas billiges wie die Additionstheoreme ins rennen schickt.
Gruß N. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 14. Juni, 2002 - 22:00: | 
|
Hallo Niels,
so hatte ich das nicht gemeint. Natürlich benutzt auch die Analysis Hilfssätze (zur Genüge!!!). Nur während du skeptisch gegenüber großen Geschütze wie komplexe Zahlen, um so etwas billiges wie Additionstheoreme herzuleiten, bist, bin ich immer skeptisch gegen geometrische Hilfskonstruktionen. Ich denke wir kommen hier zu keinem "eindeutig wahren" Ergebnis. Wenn du etwas genauer bei den komplexen Zahlen hinschaust, stellst du fest, dass diese auch eine geometrische Interpretation haben, die auch analytisch verwendet wird. Streng genommen müßte ich also auch die komplexen Zahlen anzweifeln! Für mich persönlich ist die Analysis jedoch nachvollziehbarer, weil ich sie doch etwas besser verstehen und nachvollziehen kann, während ich bei geometrischen Beweisen immer wieder in Schwierigkeiten gerate, direkt Aussagen zu folgern. D.h. nicht, dass ich es nicht kann, aber es dauert immer etwas länger weil ich jeden geometrischen Schritt mehrmals auf Einwandfreiheit überprüfe. Natürlich muss man das in der Analysis auch, aber mir fällt es wesentlich leichter.
Ich denke nicht, dass ich mir deine geometrischen Beweise ansehen muß (zu den Additionstheoremen), denn ich könnte dir aus dem Stehgreif mindestens 2 geometrische Beweise präsentieren. Wenn ich einen Beweis einmal selbstständig nachvollzogen hab, kann ich ihn meistens auch, egal ob geometrisch oder analytisch. Es ist auch nicht so, dass ich der Geometrie nicht glaube. Für mich hat die Analysis einfach einen höheren Stellenrang.
Mit freundlichen Grüssen
M. |
    
Niels (niels2)

Fortgeschrittenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 51
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 15. Juni, 2002 - 09:55: | 
|
Hi M,
Wenn du Lust hast können wir uns ja mal austauschen.
Ich sammle nämlich Beweise-Du könntest ja mal deine Beiden geometrische Beweise Skizzieren.
Mit den Komplexen Zahlen sind es 4 Beweise, mit deinen beiden könnten es 6 werden.
Gruß N. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 15. Juni, 2002 - 10:26: | 
|
Hi Niels,
im Prinzip ist das kein Problem. Nur bevorzuge ich es momentan, erst mal meine Übungsaufgaben für die Uni zu machen.
Wenn ich heute noch etwas Zeit finde, werde ich dir heute (zumindest mal einen Beweis) zukommen lassen.
Im Prinzip kenne ich drei geometrischen Beweise:
Einen elementargeometrischen (im Koordinatensystem), einen über Dreiecke (wobei ich diesen nicht ausführlich genug finde, weil im Dreieck alle Seiten >0 sind) und dann einen, der die Vektorrechnung benutzt (wobei dieser den anderen natürlich sehr ähnelt).
Im Prinzip sind alle diese Beweise sehr ähnlich.
Vielleicht sind es aber genau die Beweise, die du kennst. Kannst ja mal vergleichen.
Den Beweis über die Komplexen Zahlen habe ich oben schon geführt:
Es gilt allgemein:
e^(ix)=cos(x)+isin(x) (*)
Mit (*) =>
e^(i(x+y))=cos(x+y)+isin(x+y) (**)
Weiter gilt mit (*):
e^(i(x+y))
=[e(ix)]*[e^(iy)]
=[cos(x)+isin(x)]*[cos(y)+isin(y)]
=[cos(x)cos(y)-sin(x)sin(y)]+i[sin(x)cos(y)+sin(y)cos(x)] (***)
Aus Vergleich von Real-und Imaginärteil von (**) und (***) folgt die Behauptung!
Mit freundlichen Grüssen
M. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 15. Juni, 2002 - 16:30: | 
|
Hier mal ein Beweis:
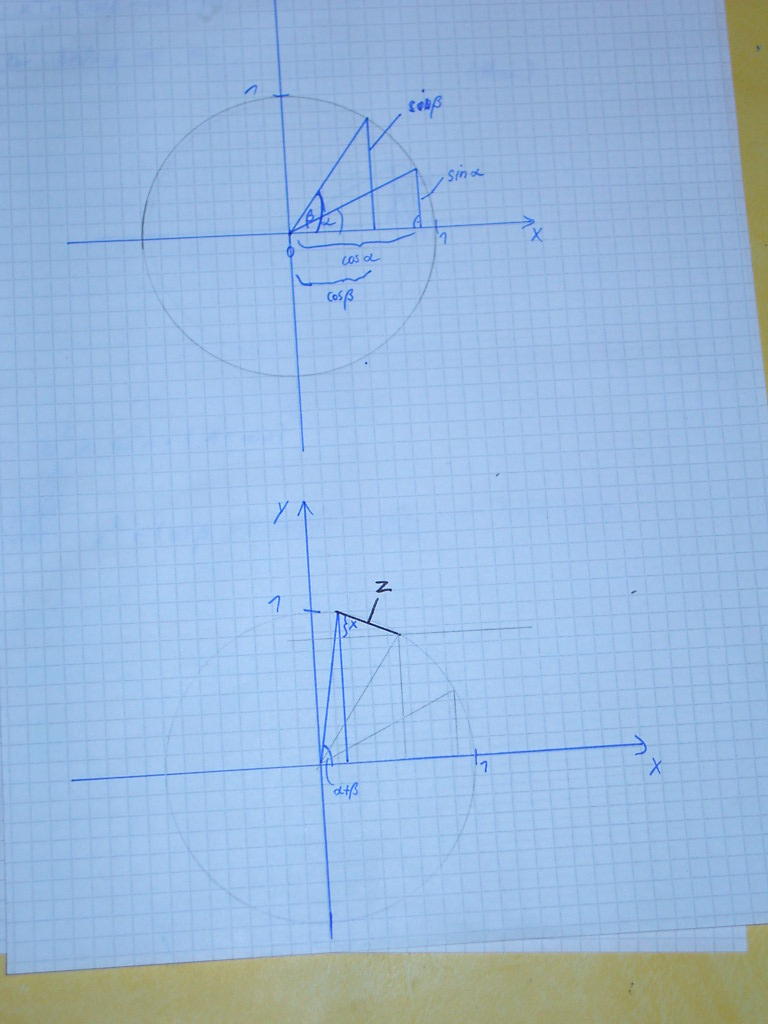 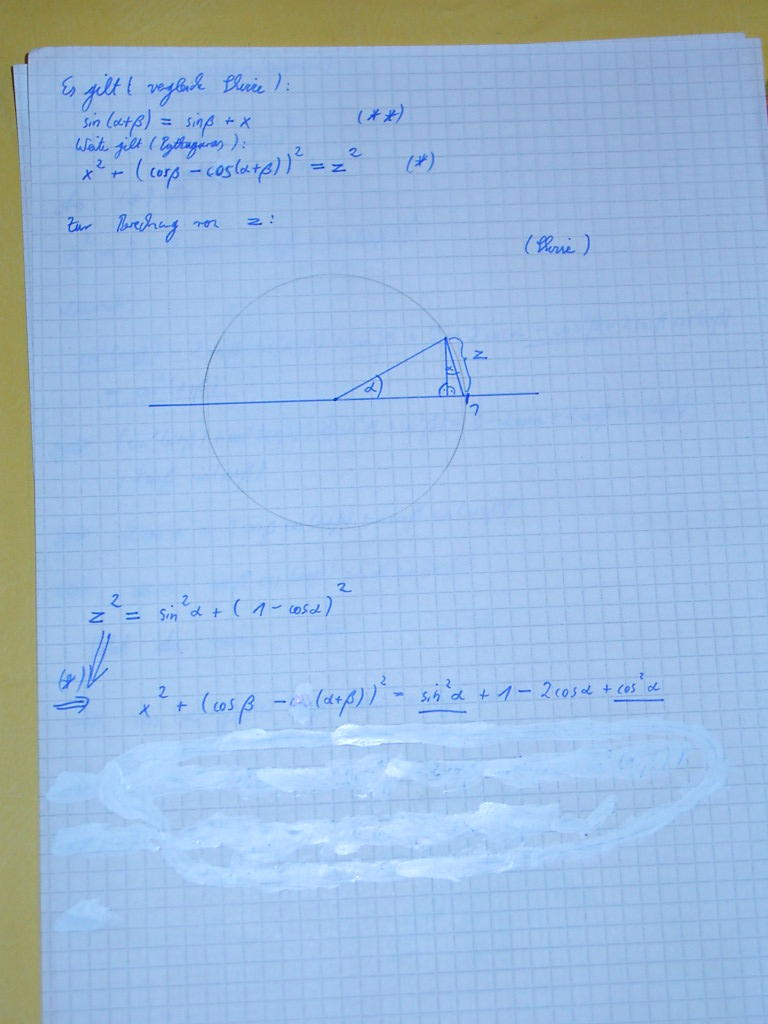 
Auf dem 2en Blatt, das mit Tip-ex verwischte, heißt:
x²+(cos(b)-cos(a+b))²=... (hier: a für alpha, b für beta)
Ich hoffe, man kann es erkennen!
Mit freundlichen Grüssen
M. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 15. Juni, 2002 - 16:32: | 
|
Komisch, hat nicht ganz geklappt, ich schicke dann die anderen beiden Bilder nach:
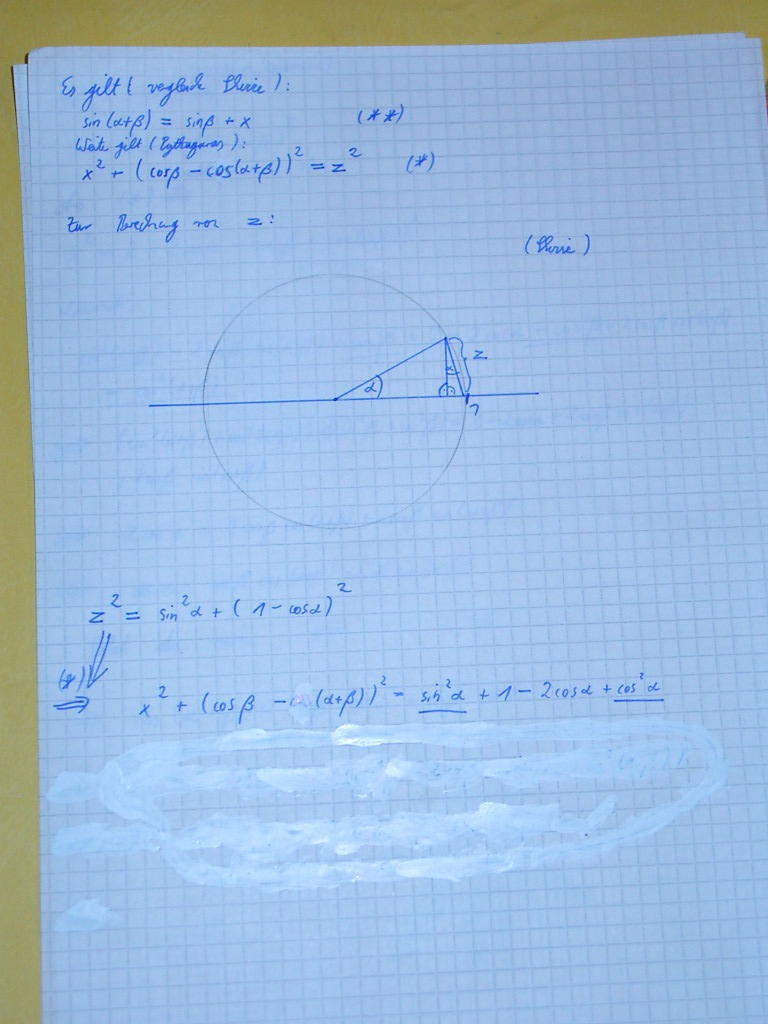 |
    
M,.

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 15. Juni, 2002 - 16:36: | 
|
Und nun das letzte:

Kleiner Fehler am Ende:
cos(a´-b)=cos(b)cos(a´)+sin(b)sin(a´) müßte es (wegen Einsetzen) heißen. Dann stimmt das Theorem nämlich auch!
Fallunterscheidungen etc. habe ich mir gespart!
Alle anderen Additionstheoreme ergben sich aus dem obigen sehr leicht!
Mit feundlichen Grüssen
M. |
    
Niels (niels2)

Fortgeschrittenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 55
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 15. Juni, 2002 - 17:48: | 
|
Hi M,
dieser "zusammengestocherte" Beweis ist mir noch nicht bekannt gewesen und wird daher in meine gloreiche Sammlung aufgenommen!
Allerdings wenn du schon mit Einheitskreis arbeitest gibt es zwei elegantere Ideen die Additionstheoreme zu beweisen.
die erste idee findest du hier:
http://www.mathematik-online.de/F98.htm#add
Die zweite idee ist folgende:
Du hast ein Punkt P auf dem Einheitskreis.Deren Koordinaten hängen nur von einem Winkel alfa ab und sind bekanntlich cos(alfa) und sin(alfa)
nun dreht man P um einen Winkel Beta und erhält über die Drehgleichungen im Cartesischen Koordinatensystem ist der Beweis nur ein Kinderspiel.
Mich fürde der Vektorielle Beweis besonders interessieren.
Gruß N. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 15. Juni, 2002 - 19:34: | 
|
Hi Niels,
aber heute bitte nicht mehr. Der vektorielle Beweis verläuft, sofern ich das in Erinnerung habe, ähnlich. Ich könnte ihn aber dennoch wahrscheinlich nicht so ohne weiteres in ein paar Minuten hinschreiben (ich tippe aber mal, dass man das Skalarprodukt benutzt). Wenn ich morgen noch Zeit finde, werde ich ihn dir zukommen lassen. Ich kenne den Beweis aus einem etwas älteren Mathebuch meines Vaters (von 1978 glaub ich ist das). Er ist in der Tat äußerst elegant, wenn man denn weiß, welche Schritte nur notwendig sind. Diese kenn ich nur momentan nicht auswendig und möchte mir dazu auch heute keine Gedanken mehr machen. Geometrische Beweise (wenn ich sie denn mal brauche) stochere ich mir übrigens immer auf diese oder ähnliche Art und Weise zusammen. Ich hatte schon mal einen (anderen) Beweis über 10 Hilfskonstruktionen mit verschiedenen Additionstheoremen etc. geführt.
PS: Der Beweis, wie er bei deinem Link aufgeführt wurde, ist meinem doch sehr ähnlich. Ich habe nur noch etwas hin- und hergerechnet, und nicht am allgemeinen Dreieck, sondern am Einheitskreis.
Mag sein, dass es eleganter geht, aber der oben aufgeführte war der erste, den ich selbstständig, d. h. ohne Hilfsmittel, geführt habe und so etwas prägt sich in mein Gedächtnis ein.
Mit freundlichen Grüssen
M. |
    
dull

Unregistrierter Gast
| | Veröffentlicht am Montag, den 17. Juni, 2002 - 10:11: | 
|
Hi!
Ich weiß nicht, ob es euch noch interessiert, aber ich habe einen sehr einfachen Beweis für beide Additionstheoreme auf einen Schlag (mit Hilfe von Funktionen und deren Ableitungen) gefunden. Man benötigt weder eine geometrische Veranschaulichung, noch komplexe Zahlen.
Falls ihr daran interessiert seid, könnte ihr das ja mitteilen. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Montag, den 17. Juni, 2002 - 15:11: | 
|
Hallo Dull,
mich interessiert es auf jeden Fall. Bin mal gespannt, wie das gehen soll!
@Niels: Immer noch interessiert an dem Beweis (über die Vektoren verlaufend)?
Mit freundlichen Grüssen
M. |
    
Niels (niels2)

Fortgeschrittenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 56
Registriert: 06-2001
| | Veröffentlicht am Montag, den 17. Juni, 2002 - 15:33: | 
|
Hi M und dull,
aber sicher bin ich noch interessiert an deinem und auch an dulls Beweis!
In freudiger Erwartung
Gruß N. |
    
DULL

Unregistrierter Gast
| | Veröffentlicht am Montag, den 17. Juni, 2002 - 17:41: | 
|
Ich hoffe, dass mein Beweis logisch korrekt ist. Ich habe ihn mir in einer deutschstunde ausgedacht 
Zuerst habe ich zwei Funktionen definiert:
f(x)=sin(x)*cos(y)+cos(x)*sin(y)-sin(x+y)
g(x)=cos(x)*cos(y)-sin(x)*sin(y)-cos(x+y)
Die Behauptung ist, dass beide Funktionen konstant 0 sind (damit sind dann ja die Additionstheoreme bewiesen).
Wenn man f und g nach x ableitet erhält man:
f'(x)=g(x)
g'(x)=-f(x)
daraus ergibt sich:
f(x)*f'(x)+g(x)*g'(x)
=f(x)*g(x)-g(x)*f(x)=0
Der Term f(x)*f'(x)+g(x)*g'(x) tritt auch auf, wenn man h(x):=1/2*(f2(x)+g2(x)) ableitet.
Dies bedeutet, dass h(x) konstant sein muss.
Jetzt setzt man einen beliebigen Wert für x ein (z.B. 0) und erhält:
h(0)=0
Also ist h(x)=0 für alle x
Daraus folgt, dass sowohl f(x) als auh h(x) gleich 0 sein müssen.
q.e.d. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Montag, den 17. Juni, 2002 - 18:16: | 
|
Hallo Dull,
also die Idee ist wirklich gut und eine typisch analytische! Ich habe es jetzt zwar nicht alles kontrolliert, aber ich glaube es dir mal.
@Niels:
Meine Kamera hat gerade den Geist aufgegeben. Mit etwas Glück kann ich dir den Beweis aber im Laufe der Woche oder am Wochenende nochmal liefern. Ich habe nur (auch wegen der Hitze) momentan keine Lust, dir eine Konstruktionsbeschreibung zu geben. Aber soweit ich das hier momentan sehe, ist im wesentlichen nur der Unterschied zu meinem Beweis, dass anstatt von Strecke AB von der Maßzahl des Vektors B-A gesprochen wird. Hab aber auch nur flüchtig draufgeguckt. Und es wird (glaub ich) etwas anders umgeformt.
Das Buch heißt übrigens:
Großes Handbuch der Mathematik
vom
BUCH UND ZEIT VERLAGSGES. M. B. H. Köln
von 1969
Beweis auf Seite 283
Vielleicht hat ja sonst noch jemand das Buch und kann den Beweis einscannen und dir offenbaren.
Mit freundlichen Grüssen
M.
PS: Bitte erinnere mich spätestens am Samstag/Sonntag nochmal(hier). Ich hoffe, dass ich es nicht vergesse!
|
    
Niels (niels2)

Fortgeschrittenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 57
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 22. Juni, 2002 - 13:30: | 
|
Hi M,
wie sieht es nun mit den vektoriellen Beweis aus?
Gruß N. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 23. Juni, 2002 - 10:39: | 
|
Hi Niels,
irgendwie läuft bei mir zur Zeit alles schief.
:-((
Nix klappt. Kamera kaputt, Batterie von der Kamera auch kaputt. Ich habe es aber nicht vergessen.
Bin zur Zeit nur etwas gestresst.
Ich hoffe, dass ich dir bis Freitag den Beweis noch liefern kann.
Aber wahrscheinlich doch mit Konstruktionsbeschreibung anstatt mit Bild.
:-(
Sorry das ich dich so lange warten lassen muss!
Aber ich bin echt im Stress!
Mit freundlichen Grüssen
M.
|
    
Sören Christensen (dull)

Neues Mitglied
Benutzername: dull
Nummer des Beitrags: 3
Registriert: 06-2002
| | Veröffentlicht am Sonntag, den 23. Juni, 2002 - 23:39: | 
|
Hi M. und Niels,
vielleicht kann sich M. seine Mühe sparen. Ich hab eben zufällig einen Beweis mit Vektoren gefunden, hab ihn allerdings noch nicht durchgeschaut. Naja, ihr könnt ja selbst mal gucken:
http://www.ksk.ch/mathematik/mathonline/mathematik/geometrie/trigfktm.pdf |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Montag, den 24. Juni, 2002 - 00:50: | 
|
Hallo Sören (dull),
ich hab ihn mir mal flüchtig angeschaut. Dieser Beweis ist besser, als den, den ich bringen wollte, weil meiner mit Maßzahlen etc. läuft. Ist halt auch ein altes Buch.
Da Niels aber Beweise sammelt, werde ich ihn dennoch bringen.
Aber erst Freitag oder Samstag.
Falls nicht wieder alles schiefläuft.
Aber ich habe zur Zeit echt Stress!
Ich hoffe, Niels ist nicht sauer deswegen. Aber dank dir, Sören, hat er ja schon einmal zumindest einen vektoriellen Beweis!
Aber solche geometrischen Beweise sind doch alle im Prinzip sehr, sehr ähnlich.
Mit freundlichen Grüssen
M. |
    
Niels (niels2)

Fortgeschrittenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 63
Registriert: 06-2001
| | Veröffentlicht am Montag, den 24. Juni, 2002 - 13:48: | 
|
Hi M und Sören,
das ist wirklich kein schlechter Beweis!
Aber wie gesagt ich sammle alles und würde mich über weitere Beweise freuen.
Sauer bin ich keinesfalls!
Gruß N. |
    
Niels (niels2)

Fortgeschrittenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 66
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 29. Juni, 2002 - 22:37: | 
|
Hi M,
nur zur Info:
Ich warte immer noch auf den versprochenen Beweis!
So leicht kommst du mir nicht davon...:-)
Gruß N.
|
    
M.

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 30. Juni, 2002 - 18:26: | 
|
Hallo Niels,
jetzt hab ich mal ein Photo in aller Hektik (und dann leider nicht allzu deutlich) hinbekommen, und dann das:
Fehler
Ein oder mehrere Dateianlagen haben das zulässige Maximum von 150 Kilobyte, das übertragen werden kann, überschritten und wurden innerhalb Deines Beitrags gelöscht. Wenn Du Dateianlagen benutzen möchtest, stelle sicher, dass Du das zulässige Maximum nicht überschreitest.
Kennst du eine Möglichkeit, wie ich das dennoch hier hereinstellen kann? Ansonsten muß ich dich wieder um eine Woche vertrösten, denn zur Zeit komme ich nur am Wochende an eine andere Kamera.
:-((
Meine ist anscheinend schrottreif! :-((
Mit freundlichen Grüßen
M. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 30. Juni, 2002 - 18:29: | 
|
PS: Das Photo hat 183 Kilobyte! |
    
Niels (niels2)

Fortgeschrittenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 67
Registriert: 06-2001
| | Veröffentlicht am Montag, den 01. Juli, 2002 - 11:43: | 
|
Hi M,
Erste Möglichkeit:
- Du nimmst die geringste Auflösung und Datenkomprimierung beim fotografieren mit der DigiCam(Bei meiner Digitalkammera wäre das auflösung 640*480 im Datenkomprimierungsformat ca 180 kb.)
- Dann speicherst du Das Bild über ein Bildbearbeitungsprogramm(z. B. Paint Shop pro) in als jpeg oder jpg Datei ab und Komprimierst bei der Abspeicherung solange bis es unter 150 kb benötigt.
Wenn alles nichts helfen sollte schicke mir das Bild per Mail!
(Einfach meinen blau markierten Namen abklicken...)
Gruß N.
|
    
M.

Unregistrierter Gast
| | Veröffentlicht am Montag, den 01. Juli, 2002 - 16:44: | 
|
Hallo Niels,
hat geklappt:

Aber wie gesagt, sehr schlechte Qualität. Kann leider vor dem Wochende nicht neu photographieren, wegen der Kamera!
Aber vielleicht kannst du es dir ja mit einem Photobearbeitungsbegramm vergrößern?
Mit freundlichen Grüßen
M. |
    
Niels (niels2)

Fortgeschrittenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 69
Registriert: 06-2001
| | Veröffentlicht am Montag, den 01. Juli, 2002 - 18:50: | 
|
Sorry M,
aber bei der Auflösung kann ich selbst mit dem besten Bildbearbeitungsprogramm nicht so groß vergrößern dass es noch lesbar wäre!
Entweder andere Kammera mit höherer Auflösung und dann per mail an mich oder du scannst es mit einen Flachbettscanner (falls du ein hast) ein.
Gruß N. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Montag, den 01. Juli, 2002 - 20:52: | 
|
Hallo Niels,
tja, dass kommt davon, wenn man in Eile ist. Werde es nochmal photographieren, dauert aber leider wieder bis zum Wochenende. Das Problem ist nicht die Auflösung der Kamera, die ist hoch genug. Ich hätte einfach näher drangehen müssen. Wird schon klappen, erinner mich halt nochmal am Wochenende dran!
Mit freundlichen Grüßen
M. |
    
sonny

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 02. Juli, 2002 - 12:40: | 
|
Etwas einfacher:
3*sin(x-pi)=2
sin(x-pi)=2/3
x-pi=arcsin(2/3)+2pi*n oder pi-(x-pi)=arcsin(2/3)+2pi*n
n ist so zu wählen, daß die Lösung in das gewünschte Intervall fällt.
sonny |
    
DULL (dull)

Mitglied
Benutzername: dull
Nummer des Beitrags: 12
Registriert: 06-2002
| | Veröffentlicht am Dienstag, den 02. Juli, 2002 - 19:23: | 
|
Hi sonny,
ich versteh den Beweis irgednwie nicht. Wäre ne 1, wenn du (oder irgendwer anders) ihn nochmal erläutern könnte. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 02. Juli, 2002 - 21:22: | 
|
Hallo dull,
welchen Beweis meinst du?
Sonnys Rechnung ist im Prinzip die selbe wie meine, nur etwas eleganter aufgeschrieben, aber leider auch unvollständig:
sin(x-pi)=2/3
=>
x-pi=arcins(2/3)+n*2pi
<=>
x=arcsin(2/3)+pi(2n+1)
Warum dies richtig ist:
sin(x*+n*2pi)=sin(x*)
Nur muß man auch beachten, dass
sin(x-pi)=sin(pi-(x-pi))=sin(2pi-x)
Also hat man auch:
2pi-x=arcsin(2/3)+n*2pi
Also auch
x=2pi(1-n)-arcsin(2/3)
Mit arcsin(2/3)=0,7297... ergeben sich folgende relevante x1,x2 Werte, die von n,n* aus Z abhängig sind:
x1=0,7297...+pi(2n+1)
x2=2pi(1-n*)-0,7297...
Nun sollen aber x1,x2 im Intervall von [0,2pi]liegen:
Mit n=1 ist x1>3pi, also muß n<1 gewählt werden.
Mit n=0 ist 0<=x1<=2pi:
Also x1=0,7297...+pi=3,8713... ist eine Lösung.
Mit n=-1 wäre x1<0, also merken wir uns die obige Lösung.
Mit n*=0 ist 0<=x2<=2pi, also:
x2=2pi-0,7297...=5,5534... ist eine weiter Lösung.
Mit n*=1 wäre x2<0 und mit n*=-1 wäre x2>2pi.
Also haben wir auch hier:
x1=0,7297...+pi=3,8713... und
x2=2pi-0,7297...=5,5534... sind die gesuchten Lösungen!
Ich hatte diese berechnet zu:
ungefähr x1=y+2pi=5,5535
und x2=3,8713
Also erhalten wir so ungefähr das selbe Ergebnis (bis auf Rundungsfehler!)!
Oder geht es um einen Beweis der Additionstheoreme?
Mit freundlichen Grüßen
M. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 02. Juli, 2002 - 21:42: | 
|
Ach, ist vielleicht nicht ganz so selbstverständlich für dich:
Die n,n* sind natürlich aus Z, d.h. ganze Zahlen!
Mit freundlichen Grüßen
M. |
    
DULL (dull)

Mitglied
Benutzername: dull
Nummer des Beitrags: 13
Registriert: 06-2002
| | Veröffentlicht am Dienstag, den 02. Juli, 2002 - 22:01: | 
|
Hi M!
Danke, mein Monitor zeigt im Moment nur blau; ich habe deswegen den Zusammenhang überhaupt nicht verstanden. Ich dachte das wäre ein vollständiger Beweis der Additionstheoreme und war etwas verwirrt.
mfG, DULL |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 02. Juli, 2002 - 22:51: | 
|
Der Monitor zeigt nur noch blau?

Versteh ich net ganz...
Ist ja auch verwirrend, wenn man 20 Beiträge zu Additionstheoreme liest und dann kommt ein (unvollständiger) Beitrag auf eine schon längst gelöste Aufgabe (nix für Ungut Sonny ; besser so als wenn sich keiner drum kümmert!). ; besser so als wenn sich keiner drum kümmert!).
Mit freundlichen Grüßen
M. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 02. Juli, 2002 - 22:55: | 
|
Ach Sorry,
ich nehm alles zurück mit der Unvollständigkeit:
Sonny hat geschrieben:
...x-pi=arcsin(2/3)+2pi*n oder pi-(x-pi)=arcsin(2/3)+2pi*n...
Habs die ganze Zeit überlesen. Ich entschuldige mich in aller Form und behaupte das Gegenteil!
Wo hab ich nur meine Brille???
Ach so, hab ja gar keine. Dann ist es aber an der Zeit!!!
Mit freundlichen Grüßen
M. |
    
Niels (niels2)

Neues Mitglied
Benutzername: niels2
Nummer des Beitrags: 1
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 07. Juli, 2002 - 12:16: | 
|
Hi M,
wie sieht es dieses Wochenede aus?
Ich bin ein ganz schön zäher Knochen, nicht war?:-)
mfg N. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 07. Juli, 2002 - 22:34: | 
|
Hi Niels,
ja, du bist ein ganz schön zäher Knochen. Manchmal glaub ich, ich hab Alzheimer. Ich dachte auch schon, ich hätte etwas vergessen, aber meinst du, mir wär eingefallen, was das gewesen wäre?
Verdammt!
Ein Glück, dass man durchs Internet nicht schlagen kann, sonst müßte ich bestimmt in Deckung gehen... ;-)
Seit wann wollte ich dir den Beweis geben:
Seit 3 Wochen? Wenn du dich nun abreagieren willst, mal vielleicht ein Hänkermännchen und schreib ´M.´ daneben.
Ich versuche, das Bild möglichst bald neu zu fotografieren. Am besten gebe ich mal keine Zeitangabe an...
;-))
Wird schon noch werden!
Mit freundlichen Grüßen
M. |
    
N.

Unregistrierter Gast
| | Veröffentlicht am Montag, den 08. Juli, 2002 - 09:27: | 
|
Hi M!
Macht ja nichts; In meiner Puppe Namens M ist noch für eine große Anzahl Nadeln Platz:-)
Ich werde von Zeit zu Zeit dich erinnern....
Gruß N. |
    
M.

Unregistrierter Gast
| | Veröffentlicht am Montag, den 08. Juli, 2002 - 13:45: | 
|
Hi Niels,
ach, du bist das! Jetzt wird mir einiges klar!
;-))
Mit freundlichen Grüßen
M. |
|





