| Autor |
Beitrag |
    
Gunter Gemmel (Gungem)

| | Veröffentlicht am Samstag, den 01. Juli, 2000 - 16:00: | 
|
Hi,
wie kann man beweisen, dass der Kreis die kompakteste Ebene Figur ist. Kompakt heisst, dass das Verhältnis aus Umfang und Fläche minimal ist. Es ist leicht zu zeigen, dass der Kreis in diesem Sinne kompakter als ein Quadrat ist, es soll aber der Beweis für alle denkbaren ebenen Figuren durchgeführt werden.
Danke |
    
Kai

| | Veröffentlicht am Sonntag, den 02. Juli, 2000 - 20:45: | 
|
Das habe ich auch schon oft gehört, daß es so ist. Und alle Aufgaben, die ich gerechnet habe bisher, waren immer ein Vergleich (Kreis/Gerade oder ...).
Und da kann man es ja (evtl. mit Integralrechnung) zeigen.
Einen allgemeinen Beweis kenne ich nicht, das Problem ist, daß man ja nicht alle Funktionentypen einzeln betrachten kann.
Mich würde die Existenz eines solchen Beweises auch interessieren, sofern existent.
Kai |
    
x-man

| | Veröffentlicht am Dienstag, den 04. Juli, 2000 - 17:25: | 
|
Hi Gunter, hast du schon mal folgenden Ansatz versucht: (nur so ein Gedanke, ohne daß ich mich damit tiefer bechäftigt hätte)
Beweise, das das Verhältnis von Umfang zu Fläche bei einem (n+1)-Eck kleiner ist, als bei einem n-Eck.
Damit hättest du quasi per "vollständiger Induktion" bewiesen, daß der Kreis (d.h. lim n -> oo) die kompakteste Figur ist. |
    
Bodo

| | Veröffentlicht am Mittwoch, den 05. Juli, 2000 - 05:49: | 
|
Den Gedanken finde ich gut, aber er alleine reicht nicht aus, da man es ja auch für nichteckige Gebilde zeigen soll. Das wird für jedes einzelne die gleiche Logik sein - aber wie allgemein beweisen?
Bodo |
    
franz

| | Veröffentlicht am Mittwoch, den 05. Juli, 2000 - 09:31: | 
|
Vielleicht indirekt: Kompakteste Figur sei irgendeine nichtkreisförmige Figur, bei der man vielleicht was abschneiden kann, kreisförmig?? F. |
    
H.R.Moser,megamath.

| | Veröffentlicht am Freitag, den 11. August, 2000 - 21:51: | 
|
Hi .
Bevor die Sommerflaute zu Ende geht, möchte ich auf die Fragen
von Gunter Gemmel et alt. von anfangs Juli etwas näher eingehen
Diese Fragen zielen offenbar auf das berühmte
isoperimetrische Problem, welches so formuliert werden kann :
M sei die Menge der ebenen einfach geschlossenen und
rektifizierbaren Kurven der Länge L.
Man bestimme diejenige Kurve aus der Menge M, für welche der
Flächeninhalt F des eingeschlossenen Bereichs maximal wird.
Als Lösung erhält man den Kreis mit dem Radius L / (2*Pi).
Eng mit diesem isoperimetrischen Problem hängt die sogenannte isoperimetrische Ungleichung zusammen:
Im Fall der ebenen Geometrie lautet diese:
F < = 4 * Pi * L ^ 2 , wobei L die Länge einer beliebigen
geschlossenen ebenen Kurve darstellt und F den Inhalt des
in ihrem Inneren liegenden Flächenteils bedeutet..
Im allgemeinen gilt die strikte Ungleichung mit dem Zeichen <,
das Gleichheitszeichen = gilt nur im Falle des Kreises.
Das Problem ist uralt ; es reicht zurück ins Altertum
Der griechische Mathematiker Zenodoros hat bereits 180 v.Chr .
das Problem erkannt und die Lösung formuliert
Ein vollständiger Beweis des Satzes ist etwas neueren Datums ;
sie gelang dem grossen Mathematiker Karl Weierstrass (1815-1897).
Vorher bemühte sich teilweise erfolgreich mit rein geometrischen
Methoden der schweiz. Mathematiker Jakob Steiner (1796 - 1863)
um den Beweis.
Sogar in der Literatur ist vom isoperimetrischen Problem implizit
die Rede.
Nach Vergil (6.Buch der Aeneis) kauft die Königin Dido zur
Gründung Karthagos Land. Zu diesen Zeck wird eine Stierhaut
in dünne Streifen zerschnitten und als zusammengeschnürtes Band
so ( kreisförmig ! ) ausgelegt, dass eine maximale Fläche
eingeschlossen wird.
Vor demselben Problem stand auch der Bauer Pachom in Tolstois
Erzählung " Wieviel Erde braucht der Mensch ? " , als man ihm
zurief: "So viel Land, wie du an einem Tag umschreiten kannst,
ist dein.".
Heutzutage ist das Problem angesiedelt in der sogenannten
Variationsrechnung, einem Teilgebiet der Analysis.
Auch hier geht es wie in der Differentialrechnung darum,
Extremalaufgaben zu lösen, jedoch liegt die Problematik darin,
dass Funktionen zu bestimmen sind ,für welche ein bestimmtes
Integral einen grössten oder kleinsten Wert annimmt.
Das Startzeichen zu diesem Zweig der Analysis gab
Johann I. Bernoulli im Jahr 1696 mit dem Brachystochronen Problem:
Es werden alle durch zwei Punkte A und B einer vertikalen Ebene
laufenden Kurvenbögen betrachtet, auf denen ein Massenpunkt
unter dem alleinigen Einfluss der Schwerkraft von A nach B
gelangen kann..
Gesucht wird diejenige Kurve, für welche die Fahrzeit minimal wird.
Die Variationsrechnung wurde weiter entwickelt und ausgebaut von
Newton, Leibniz, Johann und Jakob Bernoulli und vor allem von
Euler und Lagrange, später von Weierstrass und Ostrogradski
Schliesslich wurde die Variationsrechnung zu einer selbständigen Disziplin innerhalb der Mathematik und hat ihren festen Platz in den Vorlesungsverzeichnissen der meisten Universitäten
Variatiosprobleme (mit oder ohne Nebenbedingung) lassen sich auf Differentialgleichungen zurückführen
Dabei spielen die sog. Eulersche Differentialgleichung und die DGL von Ostrogradski eine zentrale Rolle
Ich gehe nicht näher auf eine Lösung des vorliegenden Problems mittels Variationsrechnung ein, hingegen möchte ich eine sehr schöne Lösung der Aufgabe vorführen, die von Adolf Hurwitz stammt, der von1892 bis zu
seinem Tod 1919 an der Eidgenössischen Technische Hochschule in Zürich
(damals:Polytechnikum) als Mathematiker wirkte.
Die Arbeit ist 1901 erschienen (vol. 132, p. 401-403) in den Comptes rendus des séances de l'Académie des Sciences
in französischer Sprache .Der Titel lautet :sur le problème des isopérimètres.
Hurwitz benützt zum Beweis Fourier-Reihen, und der Beweis läuft recht flott
und anschaulich ab.
Die Originalarbeit liegt vor, und ich würde mir gerne die Mühe nehmen, eine wörtliche Uebersetzung anzufertigen, wenn dies gewünscht wird.
Später veröffentlichte der bekannte deutsche Mathematiker und Buchautor
Herbert Meschkowski einen Beweis, der sich expressis verbis
auf Hurwitz bezieht.
Dieser Beweis schliesst auch die isoperimetrische Ungleichung in die Betrachtung ein.
Auch darüber könnte ich ,wenn ein Interesse vorliegt, berichten.
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
Kai

| | Veröffentlicht am Sonntag, den 13. August, 2000 - 14:34: | 
|
Hallo megamath,
Deine Ausführungen sind sehr interessant.
Der Beweis von Hurwitz von 1901 würde mich interessieren, wenn es nicht zu viel Arbeit ist, es zu übersetzen und hier reinzuschreiben.
Danke im Voraus!
Kai |
    
Zaph (Zaph)

| | Veröffentlicht am Sonntag, den 13. August, 2000 - 21:11: | 
|
Hi Megamath,
vielen Dank für die immer wieder wirklich interessanten geschichtlichen Exkurse hier am Board.
Mit dem Brachystochronen Problem (wuste gar nicht, dass das so heißt, ist das nach einer Person benannt?) kann man immer wieder gut die Leute aufs Glatteis führen:
Auf welcher Kurve gelangt ein Teilchen schnellstmöglich von A nach B?
Ich hoffe, es klappt mit der Graphik:
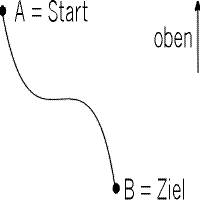
Fast jeder antwortet hier: Auf einer Gerade, denn die Gerade ist die kürzeste Verbindung zwischen A und B. |
    
Fern

| | Veröffentlicht am Sonntag, den 13. August, 2000 - 22:22: | 
|
Hi Zaph,
Griechisch:
brachy......kurz
chronos......Zeit
Die Lösung des Brachystochronen-Problems in einem konstanten Schwerefeld ist eine Zykloide.
Demnach sollten bei Kegelbahnen die Rillen zum Zurückrollen der Kugeln zykloidenförmig ausgebildet werden. Dann muss man weniger lange warten, bis eine Kugel wieder zurückkommt! |
    
H.R.Moser,megamath.

| | Veröffentlicht am Montag, den 14. August, 2000 - 08:23: | 
|
Hi Kai,
Ein hübscher Reim zu Anfang !
Hoffentlich reimen sich auch meine folgenden Ausführungen
einigermassen.
Ich nehme mir gerne die Mühe, den Beweis
von Adolf Hurwitz ins Board zu stellen.
Meine kleine Arbeit zerfällt dabei in 3 Teile.
1. Teil: eine Zusammenstellung der wichtigsten benötigten
Sätze aus der Theorie und Praxis der Fourier - Reihen.
2 .Teil  zum Aufwärmen ) eine Nacherzählung des sehr schönen zum Aufwärmen ) eine Nacherzählung des sehr schönen
Beweises von Herbert Meschkowski, der sich ausdrücklich
auf den Beweis von Hurwitz stützt.
Dieser Beweis ist im Hochschultaschenbuch B.I., Bd.51,
"Reihenentwicklungen in der mathematischen Physik",1963,
erschienen.
3.Teil: Originaltextes von Hurwitz,
zunächst in französischer Sprache
1.Teil
Eine Fourier-Reihe (F.R.) ist eine unendliche Reihe der Gestalt
f(x) = 1 / 2 * a0 + sum [an * cos(nx) + bn * sin (n*x) ] ;
der Summationsindex läuft von n = 1 bis unendlich
f(x) wird als eine periodische Funktion vorausgesetzt, z.B.
mit der Periode p = 2*Pi.
In diesem Fall wird zur Bestimmung der Fourierkoeffizienten
an, bn
über das Intervall [- Pi , Pi ] integriert; diese Koeffizienten sind:
ak = 1 / Pi * int [ f(x) * cos (k*x) * dx ] , k = 0 , 1 , 2 ..
bk = 1 / Pi * int [ f(x) * sin (k*x) * dx ] ,. k = 1 , 2 . 3 ...
Grenzen für den genannten Fall: - Pi , + Pi
Ueber die Konvergenz gilt der Satz:
Jede stückweise glatte Funktion (mit der Periode 2*Pi) lässt sich in eine
solche F.R. entwickeln, die in jedem abgeschlossenen Stetigkeitsintervall
absolut und gleichmässig konvergiert und daselbst f(x) darstellt.
Eine Funktion f(x) heisst im abgeschlossenen Intervall [a,b] der x-Achse
stückweise glatt, wenn f(x) und die Ableitung f ' (x) bis auf endlich viele Sprungstellen stetig sind.
Für f(x) und die Koeffizienten an, bn gilt die Besselsche Ungleichung:
Diese lautet:
1 / 2 * a0 ^2 + sum [an^2 + bn^2 ] < = 1 / Pi * int [f(x) ^ 2 * dx ]
Dabei läuft der Summationsindex n von 1 bis unendlich
und die Grenzen des Integrals sind die oben erwähnten.
Für die Fourierentwicklungen zweier Funktionen f(x) und g(x)
mit den Koeffizienten an, bn für f(x) und cn, dn für g(x) gilt
bei sinngemässer Reihenfolge der Koeffizienten cn, dn
die Gleichung von Parseval:
(a0 * c0) / 2 + sum [ an* cn + bn* dn ] = 1 / (Pi) * int [f(x) * g(x) *dx ]
Summationsindex und Integrationsgrenzen wie bei Bessel.
2.Teil.
Man betrachtet die Menge M der ebenen konvexen ,
einfach geschlossenen und rektifizierbaren Kurven c
von der Länge L
Gesucht wird diejenige Kurve aus der Menge M,
für welche der Flächeninhalt F des von c eingeschlossenen
Bereichs maximal ist.
Die Kurven c aus M seien durch Parameterdarstellungen
x = x(t) , y = y(t)
gegeben, wobei diese Funktionen die erwähnten
Regularitätsbedingungen erfüllen sollen.
Wesentlich ist nun die Wahl des Parameters t:
Sei t = 2 * PI * s / L ............................ (Gl I)
dabei ist wie oben vermerkt, L die Länge
der gesamten Kurve , s die von einem festen Anfangspunkt A
auf der Kurve aus gemessene Bogenlänge..
Du stellst leicht fest, dass die beiden Funktionen x(t) und y(t)
periodisch sind; sie haben beide die Periode 2* Pi.
Dies lässt sich dadurch erkennen , dass t um 2* Pi zunimmt,
wenn s durch s + L ersetzt wird.
Für x(t) und y(t) gilt dann:
x(t+2*Pi) = x(t) , y(t+2*Pi) = y(t) für alle Werte von t.
Da nun also x(t) und y(t) periodisch mit p = 2*Pi und ausserdem
im erwähnten Sinn regulär sind, lassen sich beide Funktionen in
Fourier-Reihen entwickeln,
und wir sind beim Hauptthema angelangt.
Also:
x(t) = sum [an * cos(nt) + bn * sin(n*t)]..................... .... (Gl II)
y(t )= sum [cn * cos(nt) + dn * sin(n*t)]
Wir haben der Einfachheit halber und ohne Einschränkung der
Allgemeinheit die Koeffizienten a0 und c0 je null gesetzt
Die Kurven werden durch diese Parallelverschiebung des Systems
in ihrer Struktur nicht verändert.
Jetzt differenzieren wir die beiden Gleichungen (II).
Es kommt:
x '(t) = sum [ n *{bn * cos(nt) - an * sin (nt)} ] , ............ (GL III)
y '(t) = sum [ n* {dn * cos(nt) - cn * sin (nt)}]
Gleichung (I) wird nach s aufgelöst und nach t abgeleitet :
s = L * / (2*Pi) * t
ds / dt = L / (2* Pi)............ ...................................................(Gl IV)
ds ist übrigens das Differential der Bogenlänge s ;
bekanntlich gilt: ds ^ 2 = dx ^2 + dy ^2
Nun bilden wir in (Gl IV)das Quadrat; es kommt::
(ds / dt) ^ 2 = x '(t)^2 + y ' t) ^2 = L ^ 2 / [4* (Pi ) ^ 2]......... (Gl V)
Daraus folgt für das Integral (Grenzen - Pi bis + Pi) :
int [ x'(t)^2 + y '(t)^2)] * dx = L^2 / [ 4 * (Pi)^2 ] *2 Pi
(der letzte Faktor ist gerade der Integrationsweg Pi - (- Pi ) = 2*Pi )
Somit gilt für das Integral der Quadratsumme Q der Ableitungen
Q = L ^ 2 / (2 * Pi) .... ............................................................(Gl VI)
Diesen Term verwenden wir, wenn wir auf die Gleichungen (III)
die Besselsche Ungleichung in der Form mit dem Gleichheitszeichen
anwenden
(Zusammenschluss beider Gleichungen!)
Es kommt nach Bessel
1 / Pi * int [x ' (t)^2 + y ' (t)^2 ]* dx =
= sum [n ^ 2*{an^2 + bn ^2 + cn ^2 + dn ^2 }]
Die linke Seite ist gerade Q / Pi, somit erhalten wir mit (Gl VI):
L^2 / [2*(Pi)^2] = sum [n^2*{an^2 + bn^2 + cn^2 + dn^2}] ..... (GlVII)
Für den Flächeninhalt F der von c eingeschlossenen Fläche erhalten wir
das bestimmte Integral, Grenzen - Pi., Pi:
F = int [x(t) * y '(t) * dt]
Für die Funktionen x (t) , y ' (t) ,welche als Faktoren in diesem Integral auftreten, wenden wir die Gleichung von Parseval an.
Wir erhalten:
F = Pi * sum [n*(an*dn - bn*cn)].................................................(Gl VIII)
Summation von 1 bis unendlich
Aus den Gleichungen (Gl VII) und (Gl VIII) folgt nach braver Rechnung
L^2 -4*Pi*F = 2* Pi ^2 * sum [ ( n * an - dn ) ^ 2 + ( n * cn + bn ) ^ 2 +
+ ( n ^ 2 -1 )* ( bn ^ 2 + dn ^ 2 ) ]
.......................................................................................................(Gl IX)
Der Summationsindex n läuft wiederum von 1 bis unendlich.
Ueberlegung: Die rechte Seite der Gleichung (Gl IX) wird
wegen der darin auftretenden Quadratsummen niemals negativ !!
Schluss :
Es gilt die Ungleichung:
L ^ 2 - 4 * Pi * F > = 0 .............................................................(Gl X)
Diese Ungleichung stellt die isoperimetrische Ungleichung dar,
und wir sind ein gutes Stück vorangekommen.
Wann gilt nun in dieser Ungleichung das Gleichheitszeichen ?
Offenbar genau dann, wenn für n >1 alle Koeffizienten an, bn, cn, dn
null sind, und (für n=1) a1 = d1, b1 = - c1 gilt.
Setz man diese Werte in die Gleichungen für x(t) und y(t) ein,
so erhält man die einfachen Gleichungen:
x(t) = a1* cos t + b1*sin t
y(t) = - b1* cos t + a1* sin t
Heureka ! Das ist - wie sehnlichst erwartet - eine Kreisgleichung !
Es lässt sich weiter nachweisen, dass alle rektifizierbaren Kurven
der Länge L durch Kurven der behandelten Art approximiert
werden können; damit ist das Notwendige vollbracht
Fortsetzung folgt
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
H.R.Moser,megamath.

| | Veröffentlicht am Montag, den 14. August, 2000 - 10:08: | 
|
Hi Kai ,
Es folgt nun der dritte Teil meiner Ausführungen über einen
Beweis des isoperimetrischen Problems mittels Fourier -Reihen,
nämlich
der Originaltext von Adolf Hurwitz in französischer Sprache,
erschienen in den Comptes rendus, Paris 1901:
Le problème classique:
Déterminer parmi les courbes fermées de périmètre donné
celle qui enferme une aire maximum,
peut etre(^) résolu d'une manière très simple par l'emploi des séries
de Fourier. C'est ce que je vais montrer dans les quelques lignes
qui suivent.
Soient C une courbe fermée, s la longueur de l'arc compté à partir
d'un point arbitrairement fixé sur la courbe.
Choisissons l'unité de longueur de manière que la longueur totale
de C soit égale à 2*Pi, c'est-à-dire égale a la circonférence du cercle
de rayon 1 .
Ceci posé, les coordonnées de x , y d' un point variable sur C seront
des fonctions continues de l'arc s ayant la période 2*Pi.
Supposons que ces fonctions, ainsi que leurs dérivées par rapport à s ,
soient développables en séries trigonométriques et posons
(1) x = a0 + sum [an * cos(ns) + an' * sin(ns) ],
y = b0 + sum [bn * cos(ns) + bn' * sin(ns) ] , n =1 ...inf.
L'aire F de la courbe C étant donnée par l'intégrale
F = int (x * dy) = int [x* (dy / ds ) * ds] , s = 0 ...2Pi ,
on trouve,en employant les développement (1),
(2)..........F = Pi * sum [ n* (an * bn' - an' * bn) ], n = 1...inf.
De meme(^) , en intégrant l'identité
1 = (dx/ds)^2 + (dy/ds)^2
entre les limites 0 et 2*Pi , il vient
2*Pi = int [(dx/ds)^2 * ds] + int [(dy/ds)^2 * ds ],
c'est-à-dire
(2) ..2*Pi = Pi * sum [ n^2 * {an ^2 + an' ^ 2 + bn ^ 2 + bn' ^ 2}]
Des équations (2) et (3) on tire
(4).............2 * ( Pi - F ) =
= Pi * sum {(n^2 - n)*(an^2+an'^2+bn^2 + bn'^2) +
+n* [(an-bn')^2+(an'+bn)^2]} ... n = 1....inf
Tous les termes de la dernière somme étant essentiellement positifs,
on voit que l'aire F de la courbe C ne peut pas surpasser l'aire Pi
du cercle de rayon 1.
En outre, l'égalité F = Pi entraine(^) évidemment
a1 = b1' , a1' = - b1, et an = an' = bn = bn' = 0 pour n > 1.
Par conséquent, si l'on suppose F = Pi, les équations (1) de la courbe C
prennet la forme
x = a0 + a1 * cos s + a1' * sin s ,
y = b0 - a1' * cos s + a1 * sin s,
de sorte que la courbe C est une cercle.
Donc,parmi toutes les courbes de meme(^) périmètre,le cercle,
et le cercle seul, enferme l'aire maximum.
salutations
Jean Rodolphe |
    
Zaph (Zaph)

| | Veröffentlicht am Montag, den 14. August, 2000 - 17:17: | 
|
Hi Fern, danke für die Übersetzung. In der Praxis wird die Zykloide wohl nicht die optimale Kurve für die Kegelkugelrücklaufrille sein. Denn soweit ich weiß ist das nur dann die bestmögliche Kurve, wenn die Masse punktförmig angenommen werden kann. Und bei einer Kegelkugel ist die Rotationsenergie ja nicht ganz unbeträchtlich. (Die Reibung lasse ich mal ganz aus dem Spiel.) |
    
H.R.Moser,megamath.

| | Veröffentlicht am Dienstag, den 15. August, 2000 - 14:10: | 
|
Hi allerseits,
ich möchte versuchen, hier eine Lösung
(und zwar eine von A bis B)
des Brachistochrone - Problems vorzustellen,
als ein Musterbeispiel zur Variationsrechnung.
Um uns einzustimmen, lesen wir den Anfang des Textes in den
Acta eruditorum von Johann Bernoulli aus dem Jahr 1896.
Der Text ist - wie damals in akademischen Kreisen
(für eruditi : Fachleute) üblich - in lateinischer Sprache
abgefasst und nicht schwierig zu verstehen:
Problema novum ad cujus solutionem Mathematici invitantur.
Datis in plano verticali duobus punctis A & B (vide Fig.5) Tab.V.
affignare Mobili M , viam AMB, per quam gravitate sua descendens
.....incipiens a puncto A brevissimo tempore perveniat ad alterum
punctum B.
Uebersetzung:
Hier ein Problem, zu dessen Lösung alle Mathematiker
eingeladen sind.
Zu zwei gegebenen Punkten A und B, welche in einer
senkrechten Ebene liegen (siehe Figur 5) ,Tabelle V,
ist für die bewegliche Masse M der Weg A B M zu bezeichnen,,
auf dem sie ,auf Grund ihrer Schwere herunterfällt, wenn die
Bewegung im Punkt A beginnt und in kürzester Zeit zum
anderen Punkt B gelangt,
Bei der Herleitung gehen wir die folgenden Schritte
1. Mit Hilfe geometrischer und physikalischer Gesetze stellen wir
dasjenige Integral auf ,welches die Fahrzeit T liefert
2. Aufstellen der Eulerschen Differentialgleichung zur Ermittlung
derjenigen Kurv, welche die minimale Fahrzeit ergibt
3 Lösung der Differentialgleichung zweiter Ordnung aus Punkt 2
4 Bestimmung des Kurventyps ,Diskussion.
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Zu 1
Wahl eines rechtwinkligen Koordinatensystems:
Nullpunkt in A,
x -Achse horizontal, nach rechts positiv orientiert,
y- Achsen senkrecht, nach unten positiv orientiert.
Koordinaten der beiden gegebenen Punkte: A(0/0),B(a/b)
s sei die Bogenlänge der Kurvenbogens y = y(x) der
von A nach B führt, Gesamtlänge L.
Für die Bogenlänge s = s(x) gilt bekanntlich:
ds/dx = wurzel [1 + ( y '(x) ) ^ 2 ]
Für diese Wurzel wird um folgenden eine Zeitlang
die Abkürzung w(x) gewählt
Aus dem Energiesatz 1 / 2 * m * v ^ 2 = m *g* y
.......... (g: Erdbeschleunigung, m :Masse).....
gewinnt man für die Geschwindigkeit v als Ableitung
nach der Zeit t:
v = ds / dt = wurzel (2*g*y) , eine nicht ganz unbekannte
Formel
Somit erhält man für die Fahrzeit T auf der Kurve y = y(x)
das sogenannte Funktional
T (y) = int [ dt ]; untere Grenze 0,obere Grenze T,
also der Reihe nach:
T (y) = int [ 1 / v * ds ], Grenzen 0 bis L
= int [1 / v * w(x) * dx ], Grenzen 0 bis a
= int [1 / {wurzel (2*g*y)} * w(x) * dx ], Grenzen wie soeben.
= int [wurzel ({1 + (y ' (x)^2 } / {2*g*y }) * dx ] x = 0 bis a.
Dieses Integral soll für eine zu bestimmende Kurve y = y(x)
minimal werden.
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Zu 2.
Im soeben hergeleiteten Integral lassen wir den Term
wurzel [2*g] im Nenner weg, er spielt für die Herleitung
der Eulerschen DGl keine Rolle.
Den übrig bleibenden Teil des Integranden bezeichnen wir mit F.
F ist eine Funktion der drei Variablen x, y(x) ,y '(x) ; somit
F = F ( x , y(x) , y '(x) ) = wurzel [( 1 + y ' ( x ) ^ 2 ) / y ]........ (Gl I)
In F tritt x nicht explizit auf ; für die Euler- DGl erhalten wir
daher die vereinfachte Form:
F (nach y) - F (nach y',nach y) * y ' - F (nach y',nach y') * y'' = 0 ... (Gl II)
Dabei bedeuten :
F (nach y): partielle Ableitung von F nach y
F(nach y',nach y) : zweite partielle Ableitung von F ,erst nach y',dann nach y
F(nach y',nach y') :zweite partielle Ableitung von F nach y'
Wir berechnen nun diese partiellen Ableitungen
und geben jeweils die vereinfachten Schlussresultate an
w = w(x) hat dieselbe Bedeutung wie oben
Wir erhalten durch sorgfältige Rechnung :
F(nach y) = - w / [ 2 * y * wurzel (y) ]
F(nach y ' ) = y ' / [ w * wurzel (y) ]
F(nach y',nach y) = - y' / [2 * w * y * wurzel (y)]
F(nach y',nach y') = 1 / [w ^ 3 * wurzel(y) ]
Setzt man diese partiellen Ableitung in (Gl II) ein,
so erhält man nach gehöriger , genussreicher Umformung:
die folgende Differentialgleichung zweiter Ordnung zur
Bestimmung der gesuchten Kurve y = y(x):
1 + y ' (x) ^ 2 + 2* y(x) * y ' ' (x) = 0...........(Gl III )
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Eine längere Pause ist angezeigt !
Fortsetzung folgt
Bis dann
Mit freundlichen Grüßen
H,R,Moser,megamath.
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°° |
    
H.R.Moser,megamath.

| | Veröffentlicht am Dienstag, den 15. August, 2000 - 20:16: | 
|
Brachistochrone , Fortsetzung
Zu 3.
Die zuletzt hergeleitete Gleichung (Gl III) ist eine
Differentialgleichung zweiter Ordnung, in welcher
die Variable x nicht explizit auftritt. (x-freie DGl).
Das ist ein gutes Omen; und wir können die Gleichung
ohne grosses Brimborium in eine DGl erster Ordnung
überführen.
Da y ' (x) sicherlich von null verschieden ist, dürfen wir,
ohne Schaden anzurichten, die Gleichung mit y '(x) multiplizieren
Wir erhalten:
y ' + y ' ^ 3 + 2 * y * y ' * y'' = 0
und durch eine direkte Integration:
y + y * y ' ^ 2 = K (K: Integrationskonstante)....................(Gl IV)
Man überzeugt sich von der Richtigkeit dieses Schrittes,
indem man (Gl IV) nach x ableitet und dabei die
Produktregel beachtet.
Wir ersetzen die Integrationskonstante K aus guten Gründen
durch 1 / c ^ 2 mit positivem c
Man beachte, dass die linke Seite von (Gl IV) nicht negativ
sein kann;
Also:
y + y * y ' ^ 2 = 1 / c ^2.......................................................(Gl V)
c ^ 2 * y = 1 / ( 1 + y ' ^ 2 ) ..............................................(Gl V*)
Schreiben wir die Gleichung in der Form so erkennt man, dass c ^ 2 * y
zwischen null und eins liegen muss
Es gilt: 0 < = c^2 * y < = 1
Um die so entstandene DGl erster Ordnung zu lösen, führt
man seit Olims Zeiten die folgende trigonometrische
Substitution durch :
c ^ 2 * y = [sin ( phi / 2 ) ] ^ 2 = 1 / 2 * [ 1- cos ( phi )] .....(Gl VI)
Wegen der weiter oben stehenden Ungleichung für c^2*y
ist eine solche Substitution zulässig
Ersetzt man nun gemäss dieser Substitutionsgleichung
c ^ 2 * y in (Gl V*) und löst diese nach y' auf, s
so erhält man
y ' = cot (Phi / 2) ...........................................................(Gl VII)
Wir beachten sehr wohl, dass in dieser Gleichung y ' = dy / dx
bedeutet.
Für einen späteren Gebrauch ermitteln wir aus der Gleichung
(Gl VI) die Ableitung von y nach phi ; es kommt:
dy / d(phi) = 1 / (2 * c^2) * sin(phi) ...................................(Gl VIII)
Aus der Beziehung dy / d(phi) = (dy / dx) * (dx / d(phi))
berechnen wir nun dx / d(phi) und setzen zum Schlussspurt an:
dx / d(phi) = [ sin(phi) / (2*c^2) ] * tan (phi / 2)
= [ sin(phi) / (2* c^2) ] * [(1-cos(phi)) / sin(phi)]
Somit:
dx / d(phi) = 1 / (2*c^2) * [1 - cos(phi)] ;
diese DGl lässt sich direkt integrieren:
Resultat:
x = 1 / (2* c^2) * [ phi - sin(phi)] + d
(d: weitere Integrationskonstante)
früher (Gl VI , rechts) erhielten wir bereits
y = 1 / (2*c^2) * ( 1 - cos(phi)
Die beiden Gleichungen zusammen sind eine Parametergleichung
einer Zykloide; c und d sind Integrationskonstante,die sich durch
die Bedingung bestimmen lassen,dass die Zykloide durch die
Punkte A und B geht.
Diese Rechnung lassen wir weg.
Das sollte vorerst genügen !
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
Zaph (Zaph)

| | Veröffentlicht am Mittwoch, den 16. August, 2000 - 20:14: | 
|
Hi Megamath,
habe jetzt die Muße gefunden, mir deinen Beweis zu Gemüte zu führen. Very tricky! Ich kannte zwar das Resultat, nicht aber wie man darauf kommt. Vor allem die Eulersche Dgl scheint ja ein ziemlicher Klopfer zu sein. Gibt es irgend eine Heuristik, die diese Dgl plausibel macht?
Vielen Dank
Zaph |
    
franz

| | Veröffentlicht am Freitag, den 18. August, 2000 - 16:56: | 
|
Wieviel schneller ist diese Zykloide - im Verhältnis zur geraden Verbindung AB ? franz |
    
Zaph (Zaph)

| | Veröffentlicht am Freitag, den 18. August, 2000 - 17:25: | 
|
Beliebig viel schneller! Stell dir vor, A und B liegen fast auf gleicher Höhe. Dann braucht das Teilchen auf der Geraden ewig und drei Tage. Auf der Zykloide hingegen nimmt es erst mal ordendlich Schwung, kann dann eine Weile mit Tempo die horizontale Entfernung überbrücken und wird dann wieder abgebremst. |
    
franz

| | Veröffentlicht am Freitag, den 18. August, 2000 - 21:24: | 
|
Soso .. wie sieht delta_t/t aus in Abhängigkeit von A und B? |
    
franz

| | Veröffentlicht am Freitag, den 18. August, 2000 - 23:14: | 
|
NB: Die Variationsrechnung spielt in der Physik eine wichtige Rolle, was hier nur durch Stichworte wie HAMILTONsches Wirkungsprinzip beziehungsweise LAGRANGE-Gleichungen II (Pendant der EULER-Gleichungen) angedeutet sein mag. F. |
    
H.R.Moser,megamath.

| | Veröffentlicht am Sonntag, den 20. August, 2000 - 21:22: | 
|
Hi Franz,
Du hast neulich bezüglich der Laufzeit eines Massenpunktes
längs einer Zykloide beziehungsweise längs einer Geraden
zwischen den Punkten A und B eine Frage gestellt,
die mich wieder einmal nicht ruhen liess !
Ich versuche, sie an einem numerischen Beispiel
andeutungsweise zu beantworten:
Wahl: Anfangspunkt A (0 / 0 ) , Endpunkt B( 1 / 1 )
alle Längen in Metern,
Erdbeschleunigung g = 9,81 m s ^ -2
Als Resultat ergibt sich
Fahrzeit T1 längs der Zykloide zwischen A und B:
T1 ~ 0.545 s
Fahrzeit T2 längs der Verbindungsstrecke AB :
T2 ~ 0.639 s
prozentuelle Abweichung p = (T2 - T1) / T1 * 100 ~17.25 %
Anmerkung: Die Länge der Strecke AB = wurzel(2) m
würde im Fall des freien Falls die Zeit T ' mit
T ' = 0.537 s ergeben
Es gilt .wie zu erwarten war:
T ' < T1 < T2.
Herleitung dieser Resultate in Andeutungen
(vergleiche auch meine frühere Arbeit zum
Brachistochrone - Problem vom
I.
Durch die Randbedingungen x1 = 0 , y1 = 0 für A ,
x2 = 1 , y 2 = 1 für B erhalten wir für die Konstanten
c und d in den Parametergleichungen der Zykloide
x = 1 / (2*c^2 ) * [phi - sin (phi)]
y = 1 / (2*c^2) * [1 - cos(phi)
die Werte :
d = 0
phi1 = 0 (zu A) , phi2 ~ 2.4121 (zu B)
2 * c ^ 2 = 1 - cos (phi2) ~ 1.7455
Dabei gewinnt man phi2 in einer Näherung aus der
transzendenten Gleichung
phi - sin (phi) + cos (phi) -1 = 0
Nun berechnen wir das Linienelement ds der Zykloide:
ds ^ 2 = wurzel [ x' ^ 2 + y ' ^ 2 ] * d (phi) ,
dabei sind x ' und y ' die Ableitungen
der Funktionen x(phi) , y(phi) nach phi
und d (phi ) das Differential von phi.
Wir erhalten nach leichter Rechnung für das
Differential ds der Bogenlänge:
ds = 1 / c ^ 2 * sin [ phi / 2 ] * d(phi)
Um das Differential dt der Zeit zu erhalten,
ist ds durch v, d.h. - wegen des Energiesatzes- durch
wurzel(2*g*y) zu dividieren;
es kommt der Reihe nach:
dt = 1 / v * ds = 1 / wurzel(2*g*y) * ds
= 1 / wurzel(2*g) * 2*c^2 / wurzel [{1-cos (phi)} / 2 ] * ds.
= 1 / wurzel(2*g) / sin [ phi / 2] 2c^2 * ds
Ersetzt man darin ds , so hebt sich einiges weg,
insbesondere auch c^2, und es bleibt :
dt = 1 / wurzel(2*g) * d(phi) übrig.
Gesamtzeit T = int [dt] = 1 / wurzel( 2 * g ) * int [ d(phi) ];
Grenzen im letzten Integral
untere Grenze phi1 = 0 , obere Grenze phi2 ~ 2.4121
Somit nach einfacher Integration:
T = 1 / wurzel( 2 * g ) * { phi 2 - phi 1} ~ 0.545 .
II.
Die Gerade, welche die Punkte A und B verbindet,
hat die Gleichung y = x mit y '(x) =1
Für wurzel [1+ y ' (x) ^2] erhält man daher einfach
wurzel (2)
dt wird zu dt = wurzel [ 1 + y '(x) ^2 ] / wurzel [2*g* y(x) ] * dx
= 1/wurzel [g*x] * dx ; hier ist nach x zu integrieren
und zwar in den Grenzen x = 0 bis x = 1.
Resultat: T = 1/ wurzel (g) * 2 ~ 0.6386
Ende der Vorführung und Gruss !
H.R.Moser,megamath. |
    
H.R.Moser,megamath.

| | Veröffentlicht am Montag, den 21. August, 2000 - 07:20: | 
|
Hallo Franz,
Als Nachtrag soll noch die Länge L1 des Zykloidenbogens
von A(0/0) bis B(1/1) berechnet und mit der Länge L2
der Strecke AB verglichen werden.
Als Ausgangspunkt dient die Beziehung für das Bogenelement
ds der Zykloide: ds = 1 / c^2 * sin [(phi /2 )] * d(phi)
mit c ^ 2 = 0.87275.
Für A gilt: phi 1 = 0 , für B: phi2 = 2.4121 (siehe frühere Arbeit)
Somit:
L1 = int [ ds] = 1 / c^2 * int [ sin {phi/2} * d (phi] , Grenzen
phi1 bis phi2, also:
L1 = -1 / c ^ 2 * 2 * [cos ( phi2 / 2) - cos (phi1 / 2 )] =
~ 2 / 0.87275 * [ 1 - cos (1.206) ] ~1.474 m
Mit L2 = wurzel(2) ~1.414 m erhält man die prozentuale
Abweichung q von der Streckenlänge:
q = ( L2 - L1 ) / L2 * 100 = 4,24 %
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
franz

| | Veröffentlicht am Montag, den 21. August, 2000 - 12:24: | 
|
Hallo megamath, Deine furiose Berechnung läßt meine Hoffnung auf eine Lösung des allgemeinen Falles B(x2/y2) wegen der "nur" näherungsweise phi2-Darstellung zwar schwinden (c-Elimination mittels y2/x2 ?). Doch zumindest die Idee einer beliebig flachen Bahn möchte ich noch aufgreifen B(1/D), D<<1.
d=0; phi1=0; phi2~2pi (Näh.); c² = phi2-sin(phi2)~2pi. Das Zeitintegral T-I = 2pi/Wurzel(2g) ist endlich; T-II dagegen (Laufzeit auf der geneigten Ebene / Geraden) = wurzel(2*Länge / (g*sin(Neigung)) = Länge*wurzel(2/D) wächst unbegrenzt. Gruß F. |
    
franz

| | Veröffentlicht am Montag, den 21. August, 2000 - 21:31: | 
|
Hallo Zaph, die EULER-Gleichung ebener Probleme löst das angegebene Extremalproblem: Für die Funktion f(x,y,y') ist eine Bahn yo(x) zwischen zwei festen Punkten P1 und P2 so zu bestimmen, daß das Integral x1..x2 f(x,y,y')dx im Vergleich der möglichen Bahnen einen Extremwert annimmt.
Die Idee EULERs war es, infinitesimal benachbarte Vergleichsbahnen heranzuziehen. Mit _d als Variation und D für partiell: _d INT[x1..x2] f(x,y,y')dx = INT[] _df()dx = INT[] (Df/Dy *_dy + Df/Dy' *_dy')dx = INT[] {d/dx(Df/Dy'*_dy) + (Df/Dy - d/dx Df/Dy')_dy }dx.
Der linke Term läßt sich integrieren und verschwindet wg Randbedingung; bleibt die gesuchte Beziehung Df/Dy - d/dx Df/Dy' = 0,
Physikalisches Pendant die LAGRANGE Gleichungen II: Ein System aus N Massepunkten unterliege r Nebenbedingungen gi(xj,t)=0 (i=1..r, j=1..3N), welche sich durch 3N-r generalisierte Koordinaten qk erfassen lassen (beim ebenen Pendel: statt x und y reicht der Auslenkungswinkel phi).
HAMILTON-Prinzip: Es läßt sich eine (LAGRANGE)funktion L(q,q',t) angeben (bei konservativen Kräften L=kinetische minus potentielle Energie), so daß das Wirkungsintegral int Ldt für die tatsächliche Bewegung des Systems extremal wird, respektive d/dt DL/Dq'k-DL/Dqk=0.
Anwendungsbeispiel: Bewegung in zentralsymmetrischen Kraftfeldern (KEPLER-Gesetze usw.). F. |
|





