| Autor |
Beitrag |
    
Anonym
| | Veröffentlicht am Mittwoch, den 14. Juni, 2000 - 15:04: | 
|
Hi ihr!
Wie lautet die Stammfunktion für folgende Gleichung? f(x)=xln(x^2+4)? Ich bräuchte sie wenn möglich bis morgen! Als Lösungswege habe ich bis jetzt schon partielle Integration und Integration durch Substitution ausprobiert. Bin jedoch bei beiden an der Länge gescheitert!!!
Sodass mir eine ausführliche Ansatzhilfe nur noch helfen würde!!!
Vielen Dank im vorraus; mfG C.F. |
noFEAR
| | Veröffentlicht am Mittwoch, den 14. Juni, 2000 - 15:29: |
|
hey Anonym, die Funktion leitest Du ab, indem Du die Produktregel anwendest (!!! in der Produktregel mußt Du mit der Kettenregel ableiten!!!)
=>f(x)=x*ln(x²+4)
das ist vereinfacht:f(x)=u*v [u=x, v=ln(x²+4)]
f'(x)=u'v+uv'
=>f'(x)={[x]'*[ln(x²+4]+[x]*[ln(x²+4)]'}
So jetzt die KETTENREGEL:
Du mußt ln(x²+4) folgend ableiten:
Äußere Funktion ln(...) ableiten ergibt 1/(...)
Innere Funktion x²+4 ableiten ergibt 2x
->Kettenregel Äußere * Innere Ableitung:
[1/(x²+4)]*2x ==> 2x/(x²+4)
So, jetzt in die PRODUKTREGEL einsetzen:
f'(x)=1*ln(x²+4)+[(2x²)/(x²+4)]
Ich hoffe, das ist einigermaßen verständlich, sonst Rückfragen stellen!!! |
Fern
| | Veröffentlicht am Mittwoch, den 14. Juni, 2000 - 15:40: |
|
Hallo Anonym,
I=int(xln(x²+4))dx
Partielle Integration:
u=ln(x²+4)
du/dx=2x/(x²+4)
dv=xdx
v=x²/2
I=(x²/2)ln(x²+4)-int((x²/2)2x/(x²+4))dx
int(x³/(x²+4))dx=int(x-4x/(x²+4))dx=
=x²/2+2ln(x²+4)
I=(x²/2+2)*ln(x²+4)-x²/2+C
========================== |
Christoph frenkel (Kickie)
| | Veröffentlicht am Mittwoch, den 14. Juni, 2000 - 19:10: |
|
Vielen Dank noch mal für die Hilfe!!
Aber ich wollte die Stammfkt. und nicht die Abl.!
Bei der partiellen Integration von ihnen FERN blicke ich im warsten Sinne des Wortes nicht mehr durch! Wie lautet ihre Schablone für die Lösung?
Mir ist nur: int(u`v)=uv-int(uv`) bekannt!!!
Bei der Überprüfung über Taschenrechner kann die Stammfkt nicht stimmen!
Aufg. lautete: Volumen bestimmen für Fläche zwischen Fkt ln(x^2+4) und ln8, welche sich um die y-Achse dreht! Grenze ist 2!
Für volumen von ln8(Vz) erhalte ich 26,13 bei dem Volumen für Fkt errechne ich jedoch 39,7!->?
Wobei jedoch ln8 über der Fkt liegt. Das Volumen kann nicht neg. werden! Betrag is nich.
Was nun... |
Fern
| | Veröffentlicht am Mittwoch, den 14. Juni, 2000 - 20:59: |
|
Hallo Kickie,
Du kannst ruhig du zu mir sagen.
Die Formel für die partielle Integration kann in verschiedener Form geschrieben werden auf keinen Fall aber in der von dir angegebenen.
Von mir verwendet:
ò udv=uv-ò vdu
Was die Stammfunktion von xln(x²+4) mit dem Volumen zu tun hat, sehe ich nicht. |
OliverKnieps (Oliverk)
| | Veröffentlicht am Mittwoch, den 14. Juni, 2000 - 21:37: |
|
Hallo Christoph,
das von FERN angegebene Stammfunktion ist zwar vollkommen richtig, doch würde ich hier eher die Integration durch Substitution vorziehen, denn diese ist in Deinem Fall einfach:
 Wir wählen dazu x2+4 = u und erhalten nach beidseitiger Differentiation den Ausdruck
du
-- = 2x also (1/2x)*du = dx
dx
Jetzt haben wir das dx-Integral in ein Integral mit du als Integrationsdifferential umgeformt und können durch Kürzen von x ein Grundintegral herauserkennen, nämlich
1/2*òln(u) du.
Das Integral der natürlichen Logarithmusfunktion ist Dir sicherlich bekannt, es lautet
òln(u)du = [u(ln(u)-1)]
Damit ist Dein Integral "geknackt", wir finden durch Rücksubstituion die endgültige Stammfunktion
1/2*òx*ln(x2+4)dx
= 1/2(x2+4)*(ln(x2+4)-1)
Durch Zusammenfassen ergibt sich dann FERN´s Stammfunktion.
Für die Rotation um die y-Achse musst Du die Funktion nach x2 umstellen. Das ist aber schwieriger, denn durch delogarithmieren lässt sich das x vor dem ln nicht entfernen. Beachte bitte, das die von FERN und mir angegebene Stammfunktion Dir sicherlich NICHT bei der Vy-Rotation weiterhilft, denn die Vy-Rotation ist eine Integration auf der y-Achse, welche dann neben dy auch einen nach x2 aufgelösten Ausdruck enthält, der für sich wieder integriert wird.
Für Rückfragen stehe ich gerne zur Verfügung.
Viele Grüsse
 Oliver |
OliverKnieps (Oliverk)
| | Veröffentlicht am Mittwoch, den 14. Juni, 2000 - 21:59: |
|
Hi Christoph,
nocheinmal zur Vy-Rotation:
Wir haben doch Glück, die Rotation soll, wie ich nachträglich in Deiner Nachricht gelesen habe, nur auf die Funktion
g(x) = ln(x{2}+4)
beschränkt werden.
Los geht´s
Die von Dir angegebenen Grenzen liegen bereits auf der y-Achse, es ist
y1 = ln8 und y2 = 2
Zunächst formen wir nach x2 um, damit erhalten wir
y = ln(x2+4) (delogarithmieren)
ey = x2+4 | - 4
ey-4 = x2
und wegen y1 > y2 schreiben wir direkt
pò ey-4 dy
Sicherlich stimmst Du mir zu, das dieses Integral in den Grenzen ln8 und 2 sehr einfach zu bestimmen ist. Du findest als Stammfunktion dann schliesslich:
F(y)=p[ey-4y]
und innerhalb der Grenzen ergibt sich folglich
F(ln8)-F(2)=p(8-4ln8-e2+8)=p*0,29 RE
Nocheinmal viele Grüsse und gute Nacht
Oliver |
Cosine (Cosine)
| | Veröffentlicht am Mittwoch, den 14. Juni, 2000 - 23:52: |
|
Hallo Fern!
Was ist falsch an der partiellen Integrationsformel:
int(u`v)=uv-int(uv`) ?
Anders formuliert wäre das also:
ò (u'v)dx = uv - ò (uv')dx
Setz einfach u'=du/dx und v'=dv/dx ein und Du erhälst fast Deine Version:
ò vdu = uv - ò udv
Nun zu Oliverk:
Es gibt zwei bekannte Formeln um das Volumen zu berechnen, das eine Kurve der y=f(x) ergibt, wenn sie um die y-Achse rotiert. Die eine ist die bekanntere, nämlich
V=p òy1 y2x²dy
Hier löst man normalerweise nach x auf und integriert dann nach y.
Es gibt aber auch noch eine andere, in Amiland "Shell-Method" genannte Methode mit der Formel:
V=òx1 x22px f(x) dx
Der Vorteil ist: Man muss nicht nach x auflösen, sondern kann ganz gewohnt nach x integrieren.
Und dafür braucht man dann auch die Stammfunktion von xln(x2+4) .
Deine Methode scheint mir hier trotzdem einfacher zu sein.
Ciao
Cosine |
Fern
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 07:43: |
|
Hi Cosine,
Danke dass du meine falsche Bemerkung über die Integrationsformel korrigiert hast.
Zum Volumen:
Aus den Angaben geht nicht hervor, welches Volumen gesucht wird.
Ist x=ln(8) oder y=ln(8)?
Ist die Grenze 2: x=2 oder y=2?
Am wahrscheinlichsten ist: Fläche eingeschlossen durch f(x), y=ln(8) und der y-Achse rotiert um die y-Achse.
Dies ergibt das von Oliver ermittelte Volumen (übrigens nach der Methode, die im Amiland Disc Method heißt).
Deine beiden Methoden ergeben jedoch verschiedene Volumina, nämlich einmal das Volumen der Fläche über der Kurve f(x) und einmal das Volumen der Fläche unter der Kurve. |
Cosine (Cosine)
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 10:41: |
|
Hi Fern,
Du hast natürlich Recht, dass es unterschiedliche Volumina gibt, wenn man einfach stur einsetzt, aber da mir auch nicht klar war, welches Volumen jetzt genau gesucht wird, habe ich ja auch nicht die Aufgabe bis zum Ende durchgezogen, sondern nur die beiden Methoden vorgestellt, um zu erklären, was die Stammfunktion von xln(x^2+4) mit dem Volumen zu tun hat.
Dass der von Oliver gegange Weg wohl zweifelsohne der einfachere ist, um dieses Volumen zu bestimmen, bestreite ich überhaupt nicht.
Der Vollständigkeit halber:
Wenn man die Shell-Method anweden will, so müsste das so gehen:
Shell-Method:
V= ò0 22px(ln8-ln(x2+4))dx
Nur, Oliver, ich bin der Meinung, bei Deiner Rechnung müssten die Integrationsgrenzen ln4 und ln8 sein (und nicht 2 und ln8). Damit ergibt sich dann über
Disc-Method:
V= p òln4 ln8(ey-4)dy
das gesuchte Volumen.
Ich habe beide Methoden durchgerechnet und kam in beiden Fällen zu
V=4p(1-ln2).
Ciao
Cosine |
OliverKnieps (Oliverk)
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 13:24: |
|
Hi Cosine, Fern
danke für die Nachrichten. Die Shell-Method kannte ich bisher noch nicht. Also mit Shell=Muschel mache ich mir Gedanken über ihre Herleitung...vielleicht kannst Du das mal hier posten.
Ich hätte da noch eine andere Methode zur Vy-Rotation anzubieten:
Es sei
Vy = p ò x2 dy
Bekanntlich ist dy/dx = f'(x) und nach dy aufgelöst ist dy = dx * f'(x)
Bei dieser Umformung müssen dann aufgrund der Integration nach dx die Grenzen wieder auf der x-Achse liegen. Für die Vy-Rotation finden wir dann:
Vy = p ò x2 * f '(x) dx
Auch hier gilt: Unter allen verfügbaren Methoden die schnellste heraussieben, auch im Fall der Funktion von Christoph ist die "klassische" Variante immernoch die schnellste, es gibt aber auch Funktion bei denen die obige oder die Shell-Methode schneller ist - das ist die Qual der Wahl.
Was allerdings praktisch an dieser und der Shell-Methode ist, lässt sich schnell zeigen: Wir bekommen Probleme beim Auflösen nach x2 für f(x) = x*ln(x2+4). Mithilfe der Methoden oben "umschifft" man das Problem aber sehr galant. Dann wären diese Verfahren anzuwenden. Lediglich die Stammfunktion wird dann aufwendiger.
Viele Grüsse
Oliver |
Fern
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 15:26: |
|
Zur Illustration der Shell-Methode habe ich mir die Mühe gemacht und eine kleine Skizze angefertigt:
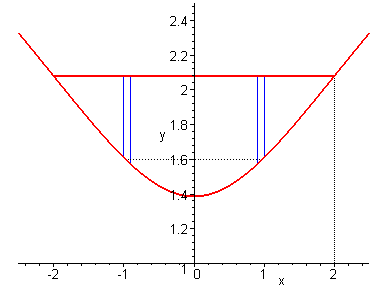
Man denkt sich aus dem Rotationskörper einen dünnwandigen (blauen) Zylinder herausgeschnitten.
Zylinderradius= x
Zylinderhöhe= ln(8)-f(x)
Wanddicke= dx
Volumen des Zylinders: 2*pi*x*[ln(8)-f(x)]*dx
Wir betrachten nun alle solchen Zylinder von Radius=0 bis Radius =2 und summieren ihre Volumina:
Gesamtvolumen = 2*pi*ò0 2x*[ln(8)-f(x)]dx
=2*pi*ò0 2x*[ln(8)-ln(x²+4)]dx= 4*pi(1-ln(2)) wie schon Cosine ermittelt hat.
====================== |
Kickie
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 16:15: |
|
Hey Leute!
Ich finde es ganz toll wie viele sich um die korreckte Lösung meines Problems gekümmert haben!!
Mit der Volumen-berechnung gibt es jedoch scheinbar Missverständnisse!
Aufg.:
Die Fkt. f(x)=ln(x^2+4) und die Gerade y=ln8 umschließen eine Fläche. Die Grenzen links und rechts ergeben sich durch das Schneiden der beiden Fkt bei x=0 und x=2! Diese eingeschloßene Fläche rotiert um die Ordinate. Berechne den Rauminhalt.
Mein Lösungsweg hieß folgendermaßen:
Ve = Vy - Vf
Vy=r^2*h*pi
=2^2 * ln8 * pi
Vf=2*pi*int(x*f(x))dx
---> Wiel bildee ich nun das Integral aus x*f(x)?
Unser Lehrer gab als Lösung an:
(meinte, Integral aus (x^2+4) ist nicht mögl.)
für x>=0 ist f(x) umkehrbar!
y = f(x) = ln(x^2+4);
e^y = x^2+4 => x^2 = e^y-4
und brechnete dann das Volumen...
V = pi int(x^2)dy und erhält ca 3,856VE
Vielen Dank nochmal für eure Hilfe! |
Fern
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 17:38: |
|
Hallo Kickie,
4*pi(1-ln(2)) = 3,856... |
Fern
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 17:43: |
|
Noch eine Bemerkung:
f(x)= ln(x²+4)
und y=ln(8)
schneiden sich nicht für x=0. |
Anonym
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 19:09: |
|
Hallo Fern,
ich habe ihre Herleitung zur Shell-Methode mit Interesse gelesen, allerdings ergeben sich da noch ein paar Fragen:
Ich verstehe die Zeichnung folgendermaßen:
- Der Abstand zwischen den blauen Linien sei die Dicke der Außenwand des Zylinders, also dx (obwohl eigentlich Dx, wegen den erst später durchgeführten Grenzwerten, aber das ist egal.
- Sei nun x der Radius des Zylinders. Wie aber gelangen Sie da zur Formel
Vz=2p*x*(ln8-f(x))* dx
Die Höhe leuchtet ein, allerdings frage ich mich warum der Radius x nicht quadriert wird und warum noch die Zahl 2 vor dem Ausdruck steht.
Es wäre nett, wenn Sie noch ein paar klärende Worte zur Herleitung geben würden!
Vielen Dank |
Fern
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 19:44: |
|
Hallo Anonym,
Ich wollte mit der Skizze nur eine Erklärung zum Merken der "shell-method" geben, nicht aber eine strenge mathematische Herleitung.
Natürlich ist der Abstand der beiden blauen Linien Dx.
Es handelt sich auch nicht um einen Zylinder, sondern um 2 konzentrische Zylinder, also um ein Rohrstück mit dem mittleren Radius=x, der Höhe = h und der Wandstärke = Dx.
(Dass die Höhe über den Bereich Dx nicht konstant ist, kann man vernachlässigen, weil beim Grenzübergang zu dx, dieser Einfluss "klein von höherer Ordnung" ist).
Um die Volumsberechnung dieses Rohrstückes besser zu verstehen, denkt man sich das Rohr entlang einer Mantellinie aufgeschnitten und dann flach aufgerollt.
So erhält man ein rechteckiges Stück mit der Dicke = Dx,
der Höhe=h und der Breite = 2*x*pi.
Das Volumen des ausgebreiteten Rohrstücks ist dann
DV = 2*x*pi*h*Dx und ist gleich dem Volumen des blauen Rohres.
Und das Gesamtvolumen:
ò dV= V = ò 2*x*pi*h*dx mit den Grenzen x=0 bis x=größter Radius.
h ist variabel und muss als Funktion von x ausgedrückt werden. |
OliverKnieps (Oliverk)
| | Veröffentlicht am Donnerstag, den 15. Juni, 2000 - 22:30: |
|
Hallo Fern,
ich habe ein bißchen in einschlägiger Fachliteratur gestöbert, aber leider keinen streng mathematischen Beweis zur Shell-Method gefunden. Wiedereinmal haben die Autoren das Problem ganz elegant umschifft, ich bemühe mich daher mal selbst um einen Beweis.
Die Höhe h der konzentrischen Zylinder sei (y1-f(x)), es sei x der Radius r des mittleren Zylinders und (x+Dx) der Radius r' des äußeren Zylinders. Das Differenzvolumen beider Zylinder bildet das Volumen des ausgebreiteten Rohrstücks. Wir bezeichnen das Volumen des äußeren Zylinders mit Z' und das des inneren mit Z. Das Differenzvolumen nennen wir ZD. Wegen Z' > Z gilt unmittelbar
ZD = Z' - Z und eingesetzt
ZD = p*(x+Dx)2*(y1-f(x)) - (p*(x)2*(y1-f(x)))
Wir erhalten ausgeschrieben dann
ZD = p*(x2 + 2xDx+(Dx)2)*(y1-f(x)) - (p*(x)2*(y1-f(x)))
Durch Ausklammern von (y1-f(x)) ergibt sich:
ZD = (y1-f(x))[p*(x2 + 2xpDx + p(Dx)2) - p*(x)2]
= (y1-f(x))[2xpDx + p(Dx)2]
Klammern wir jetzt noch p und Dx aus, so wird es wieder übersichtlicher und es bildet sich dann:
ZD = p*Dx*(y1-f(x))[2x+Dx]
Schreiben wir unendliche viele solcher Rohre in den Rotationskörper ein, so strebt deren Dicke Dx gegen 0, wird also zum Differential dx. Das bedeutet für ZD, dass das Dx in der eckigen Klammer beliebig klein und damit für die Summe in der eckigen Klammer unerheblich wird. Bildet man also formal den Grenzwert für Dx gegen 0 finden wir schließlich:
lim ZD = 2p*x*(y1-f(x))*dx
Dx ® 0
Für das endgültige Rotationsvolumen knüpfen wir hier an Ferns Lösung an, wir addieren also "unendlich oft" den Zylinder ZD ergibt sich ein Grenzwert in Form eines Integrals, nämlich Vy.
Bemerkungen:
- y1 ist bezogen auf unsere hier diskutierte Funktion dann ln8
- Für diesen Beweis unterstellt man, das der Höhenunterschied des mittleren und äußeren Zylinders mit wachsender Zylinderanzahl (also schrumpfender Dicke Dx) beliebig klein wird. Dies ist im Falle des Grenzwertes tatsächlich der Fall.
Ich hoffe sehr, das der Beweis so als "wasserdicht" angesehen werden kann.
Viele Grüsse
Oliver |
|
