| Autor |
Beitrag |
    
Janine

| | Veröffentlicht am Samstag, den 01. April, 2000 - 18:42: | 
|
Ich brauche dringend Hilfe!!!(DO.P3-Klausur und keinen Plan...)
1.) g:x=(2/6/3)+r(1/-2/-5) und die Ebene E:X=(1/4/2)+p(4/0/6)+q(-1/2/1)
a.) Bestimme die Lage der Geraden in Bezug auf die Ebene
b.) Bestimme den Schnittwinkel zwischen Gerade und Ebene
c.) Bestimme den Abstand des Punktes P(3/-4/-2) zu der Ebene
Vielen Dank ! |
    
reinhard

| | Veröffentlicht am Sonntag, den 02. April, 2000 - 09:43: | 
|
Hallo Janine!
a)
Es gibt 3 Möglichkeiten für die Lage von Geraden und Ebenen:
• parallel: der Richtungsvketor der Geraden und der Normalvektor der Ebene stehen NORMAL aufeinander und der Punkt P der Geraden LIEGT NICH in der Ebene.
• g liegt in E: der Richtungsvektor der Geraden und der Normalvektor der Ebene stehen NORMAL aufeinander und der Punkt P der Geraden LIEGT in der Ebene.
• g und E schneiden sich: der Richtungsvektor der Geraden und der Normalvektor der Ebene stehen NICHT NORMAL aufeinander.
Nun gilt es zuerst einmal den Normalvektor der Ebene zu berechnen. Dies geschieht mit dem Vektorprodukt:
n=(4;0;6)x(-1;2;1)=(0*1-6*2;-1*6-4*1;4*2+1*0)=(-12;-10;8)=2(-6;-5;4)
Nun prüfen wir, ob der normalvektor und der Richtungsvektor normal aufeinander stehen. Tun sie es, dann muß ihr Produkt 0 sein
(1;-2;-5)(-6;-5;4)=-6+10-20=-16
Also müssen sich Gerade und Ebene schneiden.
b)
Für Schnittwinkel gibt es die Formel cos(phi)=(a*b)/(|a|*|b|)
Wie du siehst, ist diese Formel nur für Vektoren geeignet, also machen wir folgendes: wir berechnen den Winkel zwischen Gerade und Normalvektor (was mit der Formel leicht geht) und der gesuchte Schnittwinkel ist dann 90° minus dem berechneten Winkel.
cos(phi)=(1;-2;-5)*(-6;-5;4)/(|(1;-2;-5)|*|(-6;-5;4)|)=16/(wuzel(30)*wurzel(77) = 0,3329
phi=70,5551°
Der gesuchte Schnittwinkel ist also 19,44°
c)
derartige Abstandsberechnungen lassen sich einfach mit der Projektion berechnen. Wenn man den Vektor a in den Vektor n projeziert, bekommt man die Länge des Vektors a in Richtung des Vektors n.
Man kann sich das so vorstellen: wenn man eine Lampe nimmt, und die im rechten Winkzel zu n hinleuchtet, dann wirft der Vektor a einen Schatten auf den Vektor n. und mit der Projektion bekommt man genau die Länge dieses Schattens.
Als a nehemen wir einen Vektor, der P mit der Ebene verbindet, also von irgendeinem beliebigen Punkt der Ebene zu P.
a=(3;-4;-2)-(1;4;2)=(2;-8;-4).
d=(a*n)/|n|
d=(2;-8;-4)(-6;-5;4)/|(-6;-5;4)|=12/wurzel(77)=1,37
Der Punkt P hat also den Abstand 1,37 von der Ebene
Reinhard |
    
Janine

| | Veröffentlicht am Sonntag, den 02. April, 2000 - 09:58: | 
|
Vielen,vielen Dank!!!
Ich hoffe ich verstehe es jetzt endlich... |
    
Eva

| | Veröffentlicht am Mittwoch, den 20. September, 2000 - 13:44: | 
|
Gegebeb sind die Greaden g: x= (2,4,2)+k ( 1,1,1) und h: x= (3,6,2)+l (1,0,2)
a) berechne den Winkel zwischen den Geraden
b) berechne die Winkel zwischen einer geraden und den Koordinatenebenen
c) gebe jeweils eiene Gleichung der Winkelhalbierenden an
d) berechne den Winkel zwischen den senkrechten Projektionen dieser Geraden un die x1x2- Ebene
e) die Geraden g und h spannen die Ebene E auf. Berechne die Winkel zwischen der Ebene E und den Koordinatenebenen
Ich bereite mich gerade auf meine klausur vor. Diese Aufgabe raubt mir allerdings den letzten Nerv. Könnt ihr mit helfen. Wäre sehr nett!!!
Bitte so schnell wie möglich!!!
Gruss Eva!!! |
    
Eva

| | Veröffentlicht am Mittwoch, den 20. September, 2000 - 13:53: | 
|
Im R3 sind die gerade g: x= (2,-2,1)+k (-1,1,1,) und die Menge E aller Punkte X (5r +s/4r/10-2s) gegeben.
a)
Zeige, dass E eine Ebene ist
b) Schneidet g die Ebene? wenn ja: Berechne die Koordinaten des Schnittpunktes S der Geraden g mit E und den Winkel zwischen gund E.h ist orthogonale Projektion von g auf E.Stelle eine Gleichung von h auf
Hinter dieser Aufgabe stand die bemerkung ( abiturprüfung 1975). Ich verstehe sie überhaupt nicht.Hab ihr Ahnung davon???
Danke im vorraus!!
Eva |
    
Fern

| | Veröffentlicht am Mittwoch, den 20. September, 2000 - 17:12: | 
|
Hallo Eva,
Hier ist der Anfang der Aufgabe:
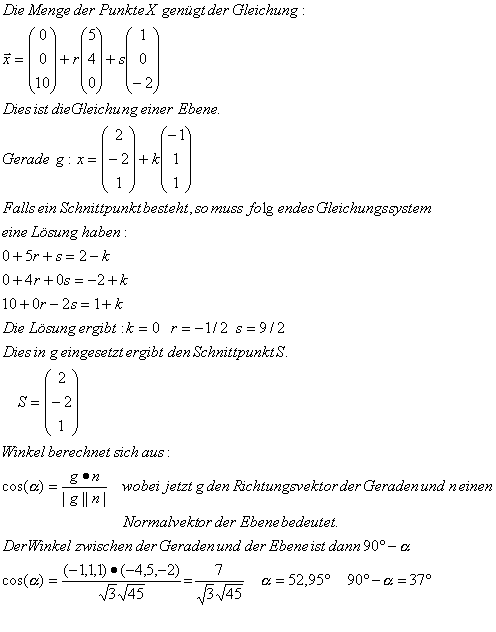
Vielleicht rechnet jemand anders weiter. |
    
Eva

| | Veröffentlicht am Mittwoch, den 20. September, 2000 - 19:39: | 
|
Ich habe noch eine Frage an Euch!
Im R3 sind die Geraden g:x= (1/-5/-1)+r(1/1/-1) und h: x=s (1/-2/5) gegeben.
a) Berechne die Koordinaten des Punktes P auf der Geraden h, welcher von g die kürzeste Entfernung hat!
b) Berechne die Koordinaten des Punktes Q, welcher zu P symmetrisch liegt bezüglich der Geraden g!!!
Dies sind nur Teilaufgaben einer grossen Aufgabe. Ich hoffe ihr könnt mir helfen!
Eva |
    
Eva

| | Veröffentlicht am Mittwoch, den 20. September, 2000 - 19:47: | 
|
Wie rechnet man eigentlich am leichtsten den Abstand eines Punktes von einer Geraden bzw. einer Ebene aus??
Wie ermittelt man den Lotfusspunkt??????
Kann man eigentlich einen Normalenvektor, wie zB (3/-6/3) kürzen auf (1/-2/1) ????
Danke Im Vorraus für eure Hilfe. Übrigens: Ihr seit echt gut!!!!
Eva |
    
H.R.Moser,megamath.

| | Veröffentlicht am Donnerstag, den 21. September, 2000 - 14:54: | 
|
Hi Eva ,
Nun wenden wir uns Deiner Aufgabe über den
kürzesten Abstand der windschiefen Geraden g
und h zu.
Es gibt eine sogenannte Minimaltransversale t ,
d.h. eine Gerade, welche g in G und h in H schneidet
und auf welcher der kürzeste Abstand d = GH liegt.
Diese Gerade t schneidet die beiden Geraden je senkrecht;
diese Tatsache werden wir ausnützen , indem wir zwei
Skalarprodukte gewisser Vektoren null setzen.
Bei Deiner Aufgabe ist zunächst "nur" der Punkt H auf h
gesucht, von dem die minimale Strecke nach dem Punkt G
auf g ausgeht
Die Aufgabe lässt sich grundsätzlich mit zwei ganz
verschiedenen Methoden lösen, die ich beide vorführen möchte.
A] mittels Vektorrechnung und analytischer Geometrie des Raumes
B] mit Hilfe der Analysis und zwar als Extremalproblem für
Funktionen mit zwei Variablen ( partielle Differentiation ).
Zu A]
Die Daten
Gerade g: "Anfangspunkt" A(1/-5/-1), Ortsvektor a = {1;-5;-1}
Richtungsvektor u = {1;1;-1} ; Parameter r
Gerade h: "Anfangspunkt" B( 0 / 0 / 0 ) , Ortsvektor b = { 0; 0 ; 0 }
Richtungsvektor v = {1 ; -2 ; 5 }; Parameter s
Zu G gehöre der Parameterwert r = r* , zu H der Parameterwert s = s*.
Diese Werte lassen sich im folgenden aus zwei Gleichungen
Ermitteln.
Der Vektor w = GH auf der Transversalen t lässt sich als
Differenzenvektor wie folgt darstellen ( O : Nullpunkt ):
w = GH = OH - OG, wobei gilt:
Vektor OH = { s* ; - 2 s* ; 5 s*}
Vektor OG = {1+ r* ; -5 + r* ; - 1 - r*}
wie sich aus den Parametergleichungen von h und g ergibt.
Wir erhalten für den Vektor w durch Subtraktionen die Darstellung
w = {s* - 1 - r* ; - 2 s* + 5 - r* ; 5s* + 1 + r* }
Die Bedingungen lauten nun
Der Vektor w steht auf den Richtungsvektoren u und v
der beiden Geraden je senkrecht , d.h. die Skalarprodukte
der Vektoren w und u einerseits und w und v andrerseits
sind null.
Wir erhalten zwei Gleichungen zur Bestimmung
der Parameterwerte s* und r*, nämlich:
(1):
s* -1 - r* - 2 s* +5 - r* -5 s* - 1 - r* = 0
vereinfacht: 2s + r = 1
(2):
s* - 1 - r* + 4s -10 + 2r + 25 s + 5 + 5r = 0
vereinfacht: 5s + r = 1
Lösungen: s * = 0 , r * = 1
s* = o liefert den gesuchten Punkt H (0 / 0 / 0 ) ;
es ist der Nullpunkt O !
Fortsetzung mit der Methode B folgt !
Mit freundlichen Grüssen
H.R.Moser,megamath |
    
H.R.Moser,megamath.

| | Veröffentlicht am Donnerstag, den 21. September, 2000 - 15:18: | 
|
Hi Eva ,
Es folgt nun eine zweite Lösungsart Deiner Aufgabe
über den kürzesten Abstand zweier windschiefer Geraden:
Wir setzen die Analysis ein , indem wir das Abstandsquadrat d^2
der beiden laufenden Punkte P auf g und Q auf h als Funktion
F = F( r, s) der Parameter r und s darstellen und
ihr Minimum berechnen
d ^ 2 = PQ ^ 2 =
F(r,s) = (s -1- r ) ^ 2 + ( - 2 s +5 - r) ^ 2 + ( 5 s + 1 + r ) ^ 2
Wir leiten diese Funktion partiell nach r und partiell nach s ab und setzen diese partiellen Ableitungen je null:
Es entstehen nach kurzer Rechnung die beiden Gleichungen
2 s + r = 1
5 s + r = 1 mit den Lösungen s = 0 und r =1
s = 0 liefert wiederum den Punkt H (0 / 0 / 0 ) auf h
wie mit der ersten Methode.
Fortsetzung mit der Spiegelungsaufgabe folgt
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
Eva

| | Veröffentlicht am Donnerstag, den 21. September, 2000 - 16:24: | 
|
Danke für die Mühe die du dir gemacht hast. Ein Weg hätte gereicht!!!
Gruss Eva!
P.S. ich werde bestimmt noch auf dich zurückkommen!!! |
    
H.R.Moser,megamath.

| | Veröffentlicht am Donnerstag, den 21. September, 2000 - 20:20: | 
|
Hi Eva,
Zu Deinem letzten Problem:
Spiegelung des Punktes P(0/0/0) an der Geraden g
g: x = 1 + r , y = - 5 + r , z = - 1 - r.
Stereometrische Lösung.
Wir legen durch P die Normalebene N (senkrechte Ebene )
zu g.
G schneidet N im Punkt S.
Der zu P bezüglich g symmetrische Punkt Q hat die Eigenschaft,
dass S der Mittelpunkt der Strecke PQ ist.
Das lässt sich leicht realisieren:
Gleichung von N : x + y - z = 0
Schnittpunkt S von g und N ( einsetzen der Koordinaten x, y, z
aus der Parameterdarstellung von g ; Auflösung nach r )
Resultat r = 1 , also :
S ( 2 / - 4 / - 2 )
Koordinaten des gesuchten Punktes so justieren,
dass die Koordinaten von S jeweils die
arithmetischen Mittel der gleichnamigen Koordinaten
der Punkte P und Q sind.
Resultat:: Q (4 / - 8 / - 4 )
Anmerkung.
1. Um den Abstand eines Punktes P von einer Geraden g
zu ermitteln, benützt man am besten die Methode der
Normalebene durch P zu g mit Schnittpunkt S wie oben.
Abstand d : Abstand der Punkte P und S
2. Der Abstand Punkt Ebene sollte grundsätzlich mit der
Hesseschen Formel unter Benützung der Normalform
der Ebenengleichung berechnet werden.
So weit !
Mit freundlichen Grüssen
H.R.Moser,megamath |
    
Eva

| | Veröffentlicht am Freitag, den 22. September, 2000 - 12:09: | 
|
Gegeben sei die Gerade g: k(1/-2).
a) Spiegele sie an der x- und y- Achse und berechne die Gleichung der Spiegelgeraden in der allgemeinen Normalenform!
b) Spiegele g: x= (1/2)+k(2/-1) an der x- Achse und an der y- Achse und bestimme die Gleichung der Spiegelgeraden.
Vielen Dank im Vorraus für Eure Hilfe!!
Es wäre super, wenn ich heute noch ein Lösungsvorschlag bekäme!!!
Eva!!! |
    
Sebastian

| | Veröffentlicht am Freitag, den 22. September, 2000 - 13:20: | 
|
Sorry, aber ich kann das elber nich! SORRY |
    
H.R.Moser,megamath.

| | Veröffentlicht am Freitag, den 22. September, 2000 - 14:54: | 
|
Hi Eva,
Wenn hintereinander zuerst an der x-Achse und danach
an der y-Achse gespiegelt wird( Bildung des sogenannten
Spiegelungsproduktes ), kann diese Produktabbildung
durch eine einzige Abbildung ersetzt werden,
in diesem Fall durch eine Punktspiegelung am Nullpunkt O.
Die gegebenen Geraden sind somit am Nullpunkt zu spiegeln.
Ihre Bilder sind zu den Ursprungsgeraden je parallel.
Rechnerisch geschieht die Punktspiegelung an O dadurch,
dass in den Gleichungen der Geraden die Variablen x und y
je durch ihre Gegenzahlen - x und - y ersetzt werden.
a ) Originalgerade g
Parameterdarstellung: x = k , y = - 2 k
Koordinatengleichung (Parameter k eliminiert) :y = - 2x
Bildgerade: g'
x = - k , y = 2k
-y = 2x oder y = - 2x
N.B. g und g' sind identisch
b) Originalgerade h
x = 1 + 2k y = 2 - k
x + 2y = 5
Bildgerade h'
-x = 1 +2 k , - y = 2 - k oder x = -1 - 2k , y = -2 + k
-x - 2y = 5 oder x + 2y = -5
Mit freundlichen Grüssen
H.R.Moser,megamath. |
    
EVA

| | Veröffentlicht am Samstag, den 23. September, 2000 - 22:33: | 
|
Danke H.R. Moser!
Du bist klasse!
Gruss Eva!!! |
    
Cinderella (Cinderella)

| | Veröffentlicht am Dienstag, den 21. November, 2000 - 08:31: | 
|
Bitte kann mir jemand helfen?
Ich muss folgende Aufgabe bis Dienstag, 28. November, lösen und habe den Durchblick völlig verloren!
Aufgabe 1
Gegeben sind die Gerade g mit dem Ortsvektor (4/-3/-1) und dem Richtungsvektor (2/-2/1) und die Gerade h mit dem Ortsvektor (-4/-1/0) und dem Richtungsvektor (3/0/-1), sowie der Punkte A (3/-1/1).
a.) Berechnen Sie den Schnittpunkt S der beiden Geraden.
b.) Geben Sie eine Normalenform der Ebene E1 an, welche g und h enthält und berechnen Sie den Abstand d (A, E1).
c.) Bestimmen Sie eine Gleichung der Ebene E2 (Koordinaten-, Normalen- oder Parameterform), welche orthogonal zur Gerade h ist und A enthält.
d.) Von A wird das Lot auf h gefällt. Berechnen Sie die Koordinaten des Punktes L, in dem sich Lot und Gerade schneiden. |
    
Cinderella (Cinderella)

| | Veröffentlicht am Dienstag, den 21. November, 2000 - 08:33: | 
|
Hier ist die zweite Aufgabe, die ich genauso dringend benötige. Im Voraus schonmal vielen Dank!Aufgabe 2
Gegeben sind der Punkt A (6/-5/3) und die Gerade g mit dem Ortsvektor (6/4/3) und dem Richtungsvektor (-2/-5/4).
a.) Weisen Sie nach, dass der Punkt A nicht auf der Geraden g liegt. Geben Sie eine Normalengleichung der Ebene E an, die durch den Punkt A geht und auf der Geraden g senkrecht steht.
b.) Bestimmen Sie den Punkt B auf der Geraden g, der vom Punkt A die kürzeste Entfernung hat.
c.) Bestimmen Sie den Punkt B auch mit den Mitteln der Differentialrechnung. (Ist X ein Punkt auf der Geraden g, so ist d (A, X) eine von k abhängige differenzierbare Funktion.)
d.) Der Punkt A1 ist der Spiegelpunkt von A bezüglich des Punktes B. Berechnen Sie die Koordinaten des Punktes A1 und die Entfernung der Punkte A und A1. |
    
Leo (Leo)

| | Veröffentlicht am Freitag, den 24. November, 2000 - 08:41: | 
|
Hallo Cinderella (schöner Name)
a) g: (x1,y1,z1)= (6,4,3) + t*(-2,-5,4)
A: (x2,y2,z2)= (6,-5,3)
Tipp: Du mußt die beiden Gleichungen gleichsetzen.
Dann hast Du 3 Gleichungen für t und mußt überprüfen, ober es eine Lösung bibt.
Skalarprodukt (a,b senkrecht=> (a.b)=0
=> ((x,y,z)-A).(-2,-5,-5)= 0
wenn Du das ausformulierst, kommt eine Normalengleichung heraus (Der Vektor,der senkrecht auf der Ebene steht, ist der Normalenvektor)
b) Der Abstand ||A-B|| zweier Punkte ist Ö((x1-x2)^2+(y1-y2)^2+(z1-z2)^2)
Daraus entsteht eine quadratische Gleichung in Abhängigkeit von t. Daraus läßt sich relativ leicht ein Minimum ermitteln und somit der Punkt B.
d)Für Spiegelung gilt: A1=B-(A-B)
und die Strecke ||A1-A|| = 2*||A-B||
versuch mal, damit zurechtzukommen, wenn Du nicht weiterkommst, kannst Du Dich gerne wieder melden. |
|





