| Autor |
Beitrag |
    
callma (callmebush)

Fortgeschrittenes Mitglied
Benutzername: callmebush
Nummer des Beitrags: 64
Registriert: 09-2002
| | Veröffentlicht am Samstag, den 15. März, 2003 - 18:56: | 
|
also ich schreibe bals Klausur und in nem anderen GK haben die in der Klausur (bei nem andren Lehrer) eine Aufgae von diesem Typ bekommen:
(nit ganz der wortlaut)
Parabel mit gleichun x:--> -x²+3
der Graph schließt mit der x - achese eine Fläche von 54 FE ein. welche zur x-Achse parallel Gerade mit g:--> c halbiert die Fläche des Graphen??
habt ihr die augabe gerafft und könnt mr beim lösen helfen????
danke schonma im vorraus!
|
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 1013
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 15. März, 2003 - 19:21: | 
|
Zeichne eine Skizze!
Die Parabel schneidet die x-Achse in a = ±Wurzel(3)
Löse -x²+3 = c ( c > 0 ),
die
Lösungen sind ±b,
nun
2*Integral[(3-x²), x = -a bis -b] + 2*c*b = 27
nach c auflösen.
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
callma (callmebush)

Fortgeschrittenes Mitglied
Benutzername: callmebush
Nummer des Beitrags: 66
Registriert: 09-2002
| | Veröffentlicht am Samstag, den 15. März, 2003 - 20:43: | 
|
wieso b und a???
für was stehen denn die, geht das ganze auch etwas kleinschrittiger? |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 1016
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 15. März, 2003 - 22:06: | 
|
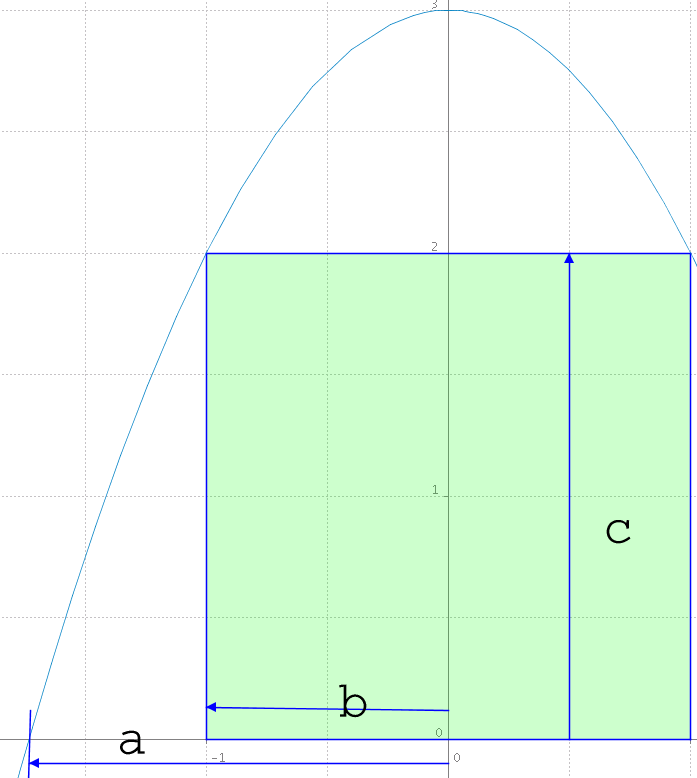
x = b ist die Lösung von -x²+3 = c
die
Fläche Integral(3-x², x = -a bis -b)
ist
die linke nicht-grüne unter dem Parabelbogen,
die tritt rechts nochmals auf.
Die grüne Fläche ist 2*b*c
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
callma (callmebush)

Fortgeschrittenes Mitglied
Benutzername: callmebush
Nummer des Beitrags: 67
Registriert: 09-2002
| | Veröffentlicht am Samstag, den 15. März, 2003 - 22:07: | 
|
ahso ok! |





