| Autor |
Beitrag |
    
Dirk21

| | Veröffentlicht am Freitag, den 21. Dezember, 2001 - 08:28: | 
|
Wer kann mir bei dieser Aufgabe helfen ,und mir Schritt für Schritt dies erklären,wie ich zum Erbebnis komme.Danke für eure Mühe.
Aus einem gegebenen Quardrat mit den Ecken ABCD bildet man wie folgt eine Pyramide. Von der Ecke A aus trägt man auf beiden Quardratseiten die gleiche Strecke s ab. Man faltet nun das Quadrat längs der Grundseite des so entstandenen gleichschenkligen Dreiecks, bis dieses auf der Grundfläche senkrecht steht. Die Dreiecksspitzen verbindet amn mit den übrigen Spitzen des Quadrats. Gesucht ist das max. Volumen der dabei entstandenen Pyramide! (wenn's geht bitte mit Skizze)
MfG
Dirk |
    
Fern

| | Veröffentlicht am Freitag, den 21. Dezember, 2001 - 10:08: | 
|
Hallo Dirk21,
Wie soll man denn bei dieser Aufgabe mit einem Kreiszylinder rechnen? Gibt es da noch weitere Angaben? |
    
Allmut

| | Veröffentlicht am Freitag, den 21. Dezember, 2001 - 11:47: | 
|
Lieber Dirk,
m.E. klappt das nicht. Wenn Du s < a/2 wählst, hat die Pyramide keine Seitenflächen; wenn Du s = a/2 nimmst, hast Du nur ein neues, kleineres Quadrat; Du kannst s auch nicht > a/2 wählen, denn dann ist nicht mehr mit falten. Also?
Oder habe ich das Problen gar nicht erkannt?
Gruß A. |
    
K.

| | Veröffentlicht am Freitag, den 21. Dezember, 2001 - 12:44: | 
|
Hallo Dirk, hallo Allmut
ich sehe das Problem genauso.
Die einzige Möglichkeit das Quadrat so zu Falten, dass die Ecken A, B, C und D zusammenfallen, besteht darin s=a/2 zu wählen. Doch die so entstehende vermeintliche Pyramide hat die Höhe h=0 und damit auch das Volumen V=0.
Es entsteht, wie Allmut schon richtig schrieb, ein kleineres Quadrat.
Mfg K. |
    
fern

| | Veröffentlicht am Freitag, den 21. Dezember, 2001 - 16:02: | 
|
Hallo allerseits,
Also ohne Kreiszylinder geht es ganz leicht:
Sei a die Seitenlänge des Quadrats.
Dann ist das Volumen der Pyramide V =(1/3)a²*h=(1/3)a²*=(1/3)a²(1/2)aÖ2
Das Volumen ist maximal wenn h maximal, also mit s=a.
hmax = (1/2)*s*Ö2
Vmax = (1/6)a³Ö2}
==================================== |
    
Fern

| | Veröffentlicht am Freitag, den 21. Dezember, 2001 - 16:42: | 
|
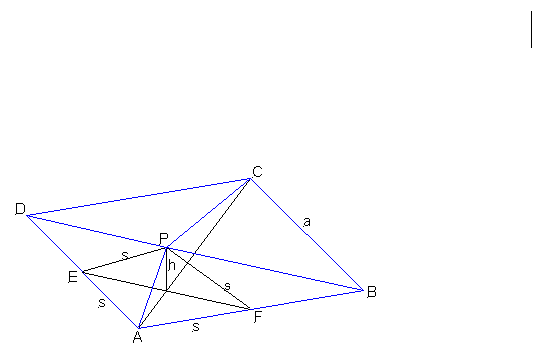
Hier die Skizze:
P........ Spitze der Pyramide
Falls s größer wird, rückt Punkt E nach D und Punkt F nach B.
Bei s = a fällt E mit D und F mit B zusammen.
 |
    
Allmut

| | Veröffentlicht am Freitag, den 21. Dezember, 2001 - 23:40: | 
|
Lieber Fern,
das verstehe ich gar nicht! Oder ist es eine Pyramide mit unterschiedlichen Seitenflächen? Scheint so. Aber das klappt bei mir auch nicht. Ich bitte um Aufklärung über Deine Erklärung hinaus.
Gruß A. |
    
Fern

| | Veröffentlicht am Samstag, den 22. Dezember, 2001 - 10:22: | 
|
Hallo Allmut,
Da gibt's eigentlich nicht viel zu erklären: ich habe nur das gemacht, was in der Angabe beschrieben ist.
Von A aus auf beiden Quadratseiten die Strecke s auftragen: dies ergibt die Punkte E und F.
Das gleichschenkelige Dreieck AFE wird nun um die Seite EF aus der Quadratebene hochgeklappt bis A in den Punkt P fällt. Das Dreieck FPE steht also senkrecht auf der Quadratebene.
Nun verbinden wir den Punkt P mit den Eckpunkten A,B,C,D.
Die Pyramide mit ABCD als Grundfläche und der Spitze P hat natürlich ungleiche Seitenflächen, die jedoch paarweise gleich sind.
ADP = ABP
BCP = CDP
==============
Das Volumen dieser Pyramide ist direkt proportional ihrer Höhe, also dann maximal, wenn h maximal ist. Dies ist der Fall, wenn s = a und P genau über dem Mittelpunkt des Quadrates liegt.
=============
Gruß, Fern |
    
Allmut

| | Veröffentlicht am Samstag, den 22. Dezember, 2001 - 11:58: | 
|
Lieber Fern,
das sehe ich immer noch nicht ein. Wenn s=a ist, dann haben wir doch den Fall eines nur kleineren Quadrats. Praktisch ist Deine Pyramide (Skizze) auch nicht zu falten., und sie hat auch nicht zwei paarweise gleiche Seitenflächen. Wenn Du das so hochknickst, entsteht keine gemeinsame Spitze -bei mir jedenfalls nicht!
Ich bin ganz ratlos.
Dirk und K., was sagt Ihr dazu?
Gruß A. |
    
Fern

| | Veröffentlicht am Samstag, den 22. Dezember, 2001 - 12:35: | 
|
Hallo Allmut,
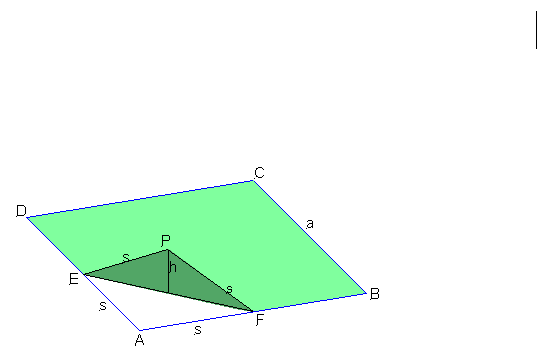
Gehen wir mal schrittweise vor:
Wir haben das Quadrat ABCD.
Nun tragen wir von A ausgehend auf den Seiten AB und AD jeweils eine Strecke mit der Länge s auf. Dies ergibt die beiden Punkte E und F.
Jetzt drehen wir das Dreieck AFE um die Drehachse EF aus der Quadratebene heraus bis es senkrecht zu dieser Ebene steht.
Das gedrehte Dreieck hat die Eckpunkte E,F und P.
=======================================
Bist du soweit einverstanden? |
    
K.

| | Veröffentlicht am Samstag, den 22. Dezember, 2001 - 21:42: | 
|
Hallo Allmut
Fern hat recht.
Wir sind die ganze Zeit davon ausgegangen, dass an allen Ecken ein Dreieck hochgeknickt und somit eine geschlossene Pyradimenform entstehen soll.
In der Aufgabe steht aber nur (mehrmaliges Lesen hat mich schlauer gemacht):
Eine Ecke hochknicken. Dadurch ist A' die Spitze einer gedachten Pyramide. Man könnte sich das vielleicht so vorstellen, dass man A' mit Hilfe eines Fadens mit den Ecken A, B, C und D des Quadrats verbindet.
Die Grundfläche ist dann das ursprüngliche Quadrat und die Höhe der Pyramide ist die Höhe im gleichschenkligen Dreieck (die hochgefaltete Ecke).
Hoffe ich konnte Dir helfen.
Mfg K. |
|





