| Autor |
Beitrag |
    
Dennis

| | Veröffentlicht am Mittwoch, den 12. Dezember, 2001 - 11:48: | 
|
Hallo
Könntet iht mir bei dieser gebrochen rationalen Kurvendiskussion helfen?
x^2+3/ x-1 |
    
Rudolf (Ruedi)

| | Veröffentlicht am Mittwoch, den 12. Dezember, 2001 - 14:29: | 
|
Hallo Dennis
Mal sehen, ob ich das alles noch zusammenkriege:
y = (x2+3)/(x-1)
1) Definitionsbereich:
Alles aus C ausgenommen x=1
2) Nullstellen:
x2+3=0 => x2=-3 => x1,2=±W(3)j
3) Extremstellen:
y' = (2x)/(x-1) - (x2+3)/(x-1)2
y' = (x2-2x-3)/(x-1)2
x2-2x-3=0 => x1=3; x2=-1
y(3) = (32+3)/(3-1) = 12/2 => y(3)=6 -> E1(3/6)
y(-1) = ((-1)2+3)/(-1-1) = 4/-2 => y(-1)=-2 -> E2(-1/-2)
y" = (2x-2)/(x-1)2 - [2(x2-2x-3)]/(x-1)3
y" = 8/(x-1)3
y"(3) = 8/(3-1)3 = 8/8 => y"(3)=1>0 => E1 ist Minimum
y"(-1) = 8/(-1-1)3 = 8/-8 => y"(-1)<0 => E2 ist Maximum
4) Wendepunkte:
y" = 0 -> keine WPs
5) Asymptoten:
Pol bei x=1
x2+3 : x-1 = x+1 +Rest
Asymptote y=x+1
6) Schaubild:
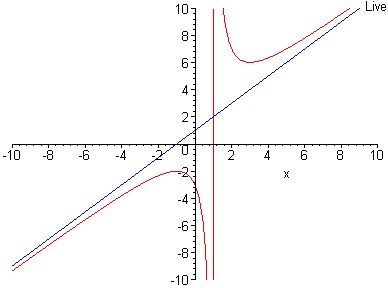
Gruss Rudolf |
    
Justin

| | Veröffentlicht am Donnerstag, den 13. Dezember, 2001 - 11:21: | 
|
Hallo Dennis, Hallo Rudolf,
Es fehlen noch drei Punkte:
=> eventuelle Symmetrieeigenschaften
=> Verhalten am Rand des Definitionsbereiches
=> Schnittpunkt mit der Y-Achse.
Das Einfachste zuerst:
Schnittpunkt mit der Y-Achse:
-----------------------------
f(0) = (0²+3)/(0-1) = -3
=> y0 = -3
Verhalten am Rand des Defintionsbereiches.
------------------------------------------
Rudolf, du hast zwar ausgeführt, dass es
eine Asymptote und eine Polstelle gibt.
Aber wie bist Du da drauf gekommen?
Ich schätze, mit einem Computerprogramm :-)
Zunächst die "Schräge Asymptote" für x=> +/- unendlich.
Der Limes für f(x) = (x²+3)/(x-1) für x=> +/- unendlich ist +/-unendlich.
Das besagt uns schon mal, dass keine "horizontale" Asymptote vorliegen kann.
Vielleicht ja eine "schräge Asymptote"?
Man führt eine Polynomdivision durch:
(x²+3) : (x-1) = x + 1 + 4/(x-1)
-(x²-x)
-------
===>x+3
=>-(x-1)
-------
=====>4
Es entsteht also die Gleichung
f(x) = x + 1 + 4/(x-1)
Und läßt man diese gegen +/+ unendlich laufen, wird der Term 4/(x-1) => NULL.
Also läuft die Funktion gegen die Asymptote
y = x + 1.
Nun die Polstelle:
Eine Polstelle liegt immer dann vor, wenn der Grenzwert der Funktion an der Stelle x0 gegen
+/- unendlich geht.
Das ist immer dann der Fall, wenn die Funktion im Nenner gleich NULL, die Funktion im Zähler
ungleich NULL ist.
Wären beide Funktionen gleich NULL, könnte man es auch mit einer Definitionslücke zu tun haben.
f(1) = (1²+3)/(1-1) = 4/0 => unendlich
Es liegt also eine Polstelle für x=1 vor, eine sogenannte "vertikale Asymptote".
Nun muss noch die Art der Polstelle bestimmt werden.
Dazu nähert man sich der Polstelle "von links" und "von rechts" und und untersucht das
Verhalten der Funktion.
limes f(x) für x=>1 bei x<1 ist MINUS unendlich
limes f(x) für x=>1 bei x>1 ist PLUS unendlich
Es kommt zu einem Vorzeichenwechsel, es liegt eine Polstelle erster Ordnung vor. Ohne
Vorzeichenwechsel läge eine Polstelle zweiter Ordnung vor.
Symmetrieeigenschaften
----------------------
Achsensymmetrie scheidet aus, denn die Funktion hat eine Polstelle, der Graph ist in zwei Äste geteilt.
Punktsymmetrie liegt aber vor, und zwar bezüglich des Punktes (1;2), in dem sich die beiden
Asymptoten schneiden.
Voraussetzung für Punktsymmetrie:
ist ein Graph bezüglich eines Punktes P(a;b) symmetrisch, dann gilt:
b - f(a-x) = f(a+x) - b
Man setzt ein, zunächst die linke Seite der Gleichung
=> 2 - ((1-x)²+3)/(1-x)-1)
= 2 - ((1² -2*1x + x² + 3) / (1-x-1))
= 2 - ((4 - 2x + x²) / (-x))
= (2x + x² - 2x + 4) / x
= (x² + 4) / x
Und nun die rechte Seite:
= ((1+x)²+3)/(1+x-1)) - 2
= (x² + 2x + 1 + 3)/(x)) - 2
= (x² + 2x + 4)/(x) - 2
= (x² + 2x - 2x + 4) / x
= (x² + 4)/x
Beide Seiten der Gleichung stimmen also überein.
Also ist die Funktion punktsymmetrisch zum Punkt (1;2)
Schönen Tag noch |
    
Rudolf (Ruedi)

| | Veröffentlicht am Donnerstag, den 13. Dezember, 2001 - 13:08: | 
|
Hallo Justin
- Ich habe die Kurvendiskussion nur gemacht, nicht erklärt.
- Okay, die Symmetrien habe ich vergessen und der Schnittpunkt mit der y-Achse auch.
- Die Polynomdivision für die schräge Asymptote habe ich gemacht.
- Das Computerprogramm brauche ich nur zum Überprüfen von Ergebnissen.
Gruss Rudolf |
|





