| Autor |
Beitrag |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 290
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 29. Januar, 2003 - 12:26: | 
|
Hallo,
ich hab hoit aus dem parallel Mathe LK gehört, das die das Volumen einer Kugel per mehrfachintegral berechnet haben!
an der tafel stand dann so etwas wie:
ò ò sqrt(1-x^2-y^2) dydx
die grenzen sind mir nicht mehr bekannt. naja meine frage ist, ob man das so machen kann und ob einer mir die idee dahinter, den weg und die lösung dann beschreiben könnte?
Vielen dank im Vorraus!
mfg |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 291
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 29. Januar, 2003 - 13:41: | 
|
also,
ich selbst schon mal geschaut:
und dabei habe ich die sog. Jacobi Formeln gefunden, für n-dimensionale Kugeln!
Vn=(pi^(n/2)*r^n)/G((n/2)+1) wobei G die Gammafunktion bezeichnet.
Man erhält dadurch wohl die Formeln:
V 2m=(pi^m*r^(2*m))/(m!)
und
V 2m+1=(2*(2pi)^m*r^(2m+1))/(1*3*5...*(2m+1))
Frage: Erhält man diese Formeln durch die Mehrfachintegrale?? Würde mich über eine Antwort freuen, da dieses Thema mich sehr interesiert!
mfg |
    
Freddy Schäfer (freddy123)

Mitglied
Benutzername: freddy123
Nummer des Beitrags: 29
Registriert: 01-2003
| | Veröffentlicht am Mittwoch, den 29. Januar, 2003 - 23:41: | 
|
Ein kleiner Exkurs über Mehrfachintegrale würde auch mich interessieren.
(Beitrag nachträglich am 30., Januar. 2003 von freddy123 editiert) |
    
Steve JK (f2k)

Fortgeschrittenes Mitglied
Benutzername: f2k
Nummer des Beitrags: 63
Registriert: 12-2001
| | Veröffentlicht am Donnerstag, den 30. Januar, 2003 - 00:15: | 
|
hallo ferdi!
hat man mit der formel auch die volumen-formel einer kugel herleiten können, oder nur auf anderem wege berechnen können??
und was sind eigentlich "mehrfachintegrale"?
was und wie rechnet man damit??
würde MICH sehr interessieren... :-)
mfg |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 295
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 30. Januar, 2003 - 12:50: | 
|
also, ich hab mich mit einem freund mal in die unterlagen geschaut, da stand folgendes:
es geht um das volumen der einheitskugel:
x^2+y^2+z^2=1
==>z=sqrt(1-x^2-y^2)
Zuerst haben sie das Volumen der Kugel als Rotationskörper berechnet:
2piò0 1 sqrt(1-x^2) dx = (4/3)pi
das geht ja noch rein, aber dann kommt meine Frage:
Volumen per Doppelintegral:
Vk=2ò ò sqrt(1-x^2-y^2) dydx
=8*ò0 1ò0 Ö(1-x²)=w sqrt(1-x^2-y^2) dydx
=8*ò0 1ò0 w sqrt(w^2-y^2) dydx
=8*ò0 1 (w^2/2)*(pi/2) dx
=8*(pi/4)*ò0 1 1-x^2 dx
=(4/3)pi
Das meinet ich! Kann mir einer die Idee dahinter, den Weg (mein freund versteht den auch nicht!!) und die Lösung allgemein erklären?
beim zeiten doppelintegral soll die obere grenze sqrt(1-x^2)=w heißen! kann er irgendwie nich darstellen!
Danke
mfg
(Beitrag nachträglich am 30., Januar. 2003 von tl198 editiert) |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 297
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 30. Januar, 2003 - 14:36: | 
|
Hi Ferdi,
ich glaube ich habe es durchschaut:
hier nochmal der Rechenweg etwas ausführlicher, ich hoffe du checkst das System, sonst kommentiere ich es gerne.

Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 296
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 30. Januar, 2003 - 15:45: | 
|
Danke Niels,
aber weist du mehr über die Idee die dahinter steht, oder warum man vom ersten zum zweiten Integral statt der 2 eine 8 als Konstante vorm Integral stehen hat?? Auch was die Gammafunktion mit dem Volumen im n-dimensionalen zu tun hat (Jacobi Formeln) würde mich interessieren!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 298
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 30. Januar, 2003 - 16:56: | 
|
Hi Ferdi,
ja, ich habe es verstanden; folgendes:
z=f(x;y)=sqrt(1-x^2-y^2)
beschreibt nur die ober hälfte der Kugel.
Will man das ganze Kugelvolumen berechnen muss man das Doppelintegral mit 2 multiplizieren!
Weiter zur Theorie der Doppelintegrale:
Wir wollen Versuchen nun das Kugelvolumen mit hilfe von "rechteckiger Säulen" zu berechnen.
Änlich wie bei der Flächenberechnung mit Integralen:
Bei der Flächenberechnung summiert man Rechteckflächen auf und erhält im Fall unendlich vieler Rechteckflächen die gesuchte gesammtfläche.
Nun wollen wir das Kugelvolumen berechen indem wir die Volumina unendlich vieler "rechteckiger säulen" zu berechnen.
Dann tun wir das mal:
Die Fläche einer solchen "rechteckigen säule"
sei deltaAkdie höhe der Säule
ist zk=f(xk;yk)
Das Volumen ist :
deltaV=zk*deltaAk=f(xk;yk)*deltaAk
Nun kommt die Summation:
V=S n k=1deltaV=Sn k=1f(xk;yk)deltaAk
lassen wir nun n gegen unendlich streben strebt deltaAk=Deltaxk*deltaYk gegen Null wir schreiben dafür dA=dx*dy=dy*dx.
Falls also dieser Grenzwert existiert, so wird er als "Doppelintegral" bezeichnet und durch das symbol:
ò ò f(x;y)*dA
(A)
ò ò f(x;y)*dy*dx
(A)
soweit erstmal, Fortsetzung folgt später...
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 299
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 30. Januar, 2003 - 18:47: | 
|
Aha, langsam lichtet sich das Dunkel. Warte schon auf deinen nächsten Beitrag.
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 299
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 30. Januar, 2003 - 20:52: | 
|
Hi Ferdi, leider habe ich heute Abend nicht mehr genug Zeit für weitere Ausführungen. Du musst dich bis Morgen Vormittag gedulden.
Nur soviel.
Wir bewegen und wenn wir eine Funktion z=f(x;y) haben im 3D Koordinatensystem. Ein Kartesisches Koordinatensystem mit 3 Achsen, Teilt den Raum in 8 Quadranten. Da wir uns bei der Volumenberechnung der Kugel auf ein Teil der Kugel konzentrieren wollen- Bedenke dass Der Mittelpunkt der Einheitskugel M(0;0;0) also der Ursprung ist-wir wollen uns nähmlich nur Auf den Quadranten x>0;y>0=>z>0 bekommen wir bei der Volumenberechnung nur 1/8 des Vollen normalen Kugelvolumens.
Daher kommt die 8 vor das Doppelintegral!
Gruß N.
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 300
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 31. Januar, 2003 - 11:10: | 
|
So, jetzt soll es weiter gehen im kleinen "Exkurs Doppelintegrale":
Wir sind nun zu der 2. Zeile vorgestoßen:
Vk=8*ò0 1ò0 Ö(1-x²)=w sqrt(1-x^2-y^2) dydx
Die Funktion ist klar, die 8 habe ich auch erklärt. Nun zu den Grenzen:
Für
Z=f(x;y)=sqrt(1-x²-y²) gilt:
Da die Funktion nur für positive Wurzeln definiert ist-Man beachte, das wir 2 reelle Variablen x und y haben-gilt für x und y:
x²+y²=<1 bzw y²=<1-x² woraus folgt:
y=<Ö(1-x²)
D.h. wir haben in der Koordinatensystem die Intervalle
für x Element [0;1] und y in abhängigkeit von x; y Element [0;Ö(1-x²)
Im Fall y=1-x² beschreibt y den Viertelkreisbogen in der x;y Ebenen. Damit sind die Grenzen erstmal erklärt.
Nun zu unserem Volumen,
Wir machen dies Schrittweise:
Wenn wir unendlich viele Säulen in unser Kugel quetschen wollen, so tun wir dies in 2 Schritten:
Wir summieren erst alle säulen in y-Richtung auf und erhalten dann eine "Volumenscheibe" der dicke dx und Summmieren dann alle "Volumenscheiben" in x-Richtung auf und erhalten das Gesammtvolumen.
Summation bis unendlich heißt für uns Integration.
summation=Integration. Nicht um sonst nennt man Integrale auch "Summengrenzwerte".
Das heißt, wir müssen nun erstmal innen Integriren.
"Innen integrieren" bedeutet hier die Funktion
z=f(x;y) nach y zu integrieren, x spielt hier keine Rolle und hat die Funktion einer normalen Konstanten, eines Parameters und wird also wie ander konstanten in dem Funktionsterm behandelt. Alleinige Integrationsvariable ist im Moment y !
wir berechnen nun also das "Innere Integral"
ò0 Ö(1-x²)=wsqrt(1-x^2-y^2)dy
eigentlich müsste als untete Grenze y=0 und als obere Grenze y=Ö(1-x²) stehen, spielt aber hier keine Rolle. Da x bei der integration die Rolle eines Parameters also einer üblich en Konstanten übernimmt können wir Ö(1-x²)=w setzen.
unglaublicherwise ist Ö(1-x²)=w dadurch ist w²=1-x² und somit für den Ausdruck 1-x² ind die Ausgangsfunktionsgleichung einsetzbar. Und das Integrál sieht dann so aus.
ò0 wsqrt(w²-y²)dy
y ist wie gesagt die Integrationsvariable, y Element [-|w|;|w|] und w Element R{0}. Und hierzu sollte sich eine hübsche Stammfunktion finden lassen!
soweit erstmal....
Mindestenz ein Beitrag kommt noch! bis Später!
Gruß N.
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 301
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 31. Januar, 2003 - 11:37: | 
|
Ich habe es mir anders überlegt, was haltet ihr davon, wenn das Thema noch ein wenig ausgedehnt wird. Mit Mehrfachintegralen kann man tolle sachen machten-nicht nur volumina betechnen!
Mir schwebt vor beispielsweise die Kreisfläche und Ellipsenfläche per Doppelintegral zu berechenn. Was denkt ihr darüber? Wolle nwir die Kreisfläche mit 2 Integralen in die Zange nehmen und zerquetschen?
Gruß N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 301
Registriert: 10-2002
| | Veröffentlicht am Freitag, den 31. Januar, 2003 - 11:59: | 
|
Also,
erst einmal möchte ich dir für deine Ausführliche Erklärungen danken! Nun haben Mehrfachintegrale auch einen Sinn für mich!
Ich würde es begrüßen den Exkurs noch weiter auszudehnen! Man kann nie genug wissen!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 302
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 31. Januar, 2003 - 13:04: | 
|
Hi Ferdi,
no Problem, mach ich doch gerne!
Weiter gehts im Text:
ò0 w sqrt(w²-y²)dy
Eine Stmaafunktion ist:
(y/2)*Ö(w²-y²)+(w²/2)*arcsin(y/w)
setzt man obere Grenze W ein so ergibt der Term
(w²/2)*arcsin(1)=(w²/2)*(p/2)=w²*p/4
für untere Grenze 0 in die Stammfunktion eingesetzt wird der Term Null. Es bleibt also nur das Integral:
ò0 1w²*p/4 dx übrig.
Den Faktor p/4 können wir vor das Integrla ziehen und mit der 8 die immer noch bei uns im Hinterkopfrumschwirrt verrechnen. Ergebnis:
vk=2p*ò0 1w² dx
Nun wissen wir das w²=1-x² gilt. für w bekommen wir also eine Funktion mit variable x.
vk=2p*ò0 1(1-x²)dx
Und das einfache Integral berechnent ergibt mit 2\greek7p} multipliziert das Kugelvolumen der Einheitskugel, nämlich (4/3)*pi !
q.e.d
================================================
Anmerkungen:
Wir erwitern die Aufgabe und wollen das Volumen einer allgemeinen Kugel auf analoge weise herleiten. Dazu sind nur ein paar "Modifikationen" notwendig.
mehr dazu später!
N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 302
Registriert: 10-2002
| | Veröffentlicht am Freitag, den 31. Januar, 2003 - 13:30: | 
|
Hi Niels,
ich kann es mir schon denken!
wir nehmen einfach die Kugel x^2+y^2+z^2=r^2
und schreiben dann mit Ö(r^2-x^2)=t
8*ò0 r ò0 t Ö(t^2-y^2) dydx
das liefert dann das wohl bekannte (4/3)pi*r!!
Naja, freue mich auf deine weiteren ausführungen!
mfg |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 303
Registriert: 10-2002
| | Veröffentlicht am Freitag, den 31. Januar, 2003 - 22:23: | 
|
uups,
ich seh grad in meinen unterlagen, das sich da ein schreibfehler eingeschlichen hat!
es muss natürlich heißen (4/3)*p*r^3.
ich warte schon auf deine anregungen bezüglich doppelintegralen und ellipsen!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 303
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 31. Januar, 2003 - 22:37: | 
|
Hi Ferdi,
du hast vollkommen recht mit deinem Ansatz!
Hier habe ich nochmal den Rechenweg komplett aufgeschrieben- die Modifikationen müßten einem im Vergleich zur Rechnung für die Einheitskugel auffallen...
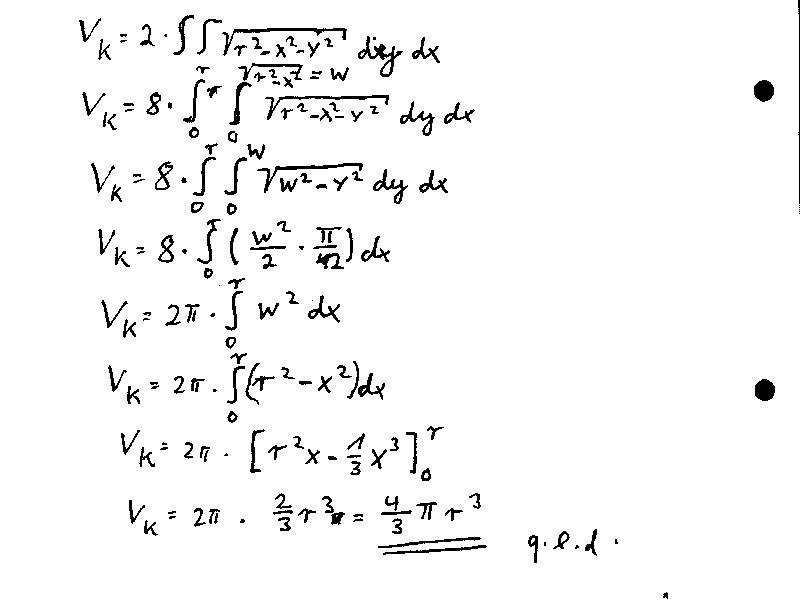
Wie erwünscht kommt das alt bekannte Ergebnis heraus!
Im nächsten Beitrag sind noch ein paar allgemeine Anmerkungen zur Berechnung von Doppelintegralen vorgesehen und dann denke ich kommen wir zur Flächenberechnung.
Bis dann.
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 304
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 01. Februar, 2003 - 10:36: | 
|
Hi Ferdi,
was hiltest du davon das Volumen eines Ellipsoiden per Doppelintegral zu berechnen?
Und nachdem wir dann ein paar Flächen berechnet haben könnten wir noch weiter gehen.
Wir könnten mit folgender Aufgabe den Vogel anschießen.
Berechnung des Volumens einer Kugel per "Dreifachintegral"...
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 305
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 01. Februar, 2003 - 13:39: | 
|
H Ferdi, nun folgen ein paar allgemeine Anmerkungen zur Berechnung von Doppelintegralen:
Anmerkungen
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
1]
Bei der Integration eines Doppelintegrals wird von innen nach außen Integriert.
ob zuerst nach y oder x integriert wird hängt von der Reinfolge der differentiale ab.
Das Integral
òx=a bòy=fu(x) fo(x)f(x;y)dydx
wird wiefolgt Integriert:
òx=a bòy=fu(x) fo(x)f(x;y)dydx
erst wird also das rote innere Integral nach y integriert. Die Grenzen des inneren roten Integrals sind Funktionen in x. wobei x als konstante angesehen wird. Danach wir das Blaue Integral gelöst. Die Grenzen des Blauen äußere Integrals sind dormale konstanten, Zahlen.
Das Integral:
òy=a bòx=gu(y) go(y)f(x;y)dxdy
wird wiefolgt berechnet:
òy=a bòx=gu(y) go(y)f(x;y)dxdy
Bei diesem Integral wird erst das rote innere Integral nach x integriert. Die Grenzen des roten Integrals sind normalerweise Funktionen in y, wobei y als konstanter Paramerter angesehen wird. Danach wird das blaue aüßere Integral nach y integriert. Die Grenzen sind wieder normale Zahlen, sprich Konstanten.
wie gesagt, die Reihenfolge wonach zuerst Integriert wird hängt von der Reihenfolge der Differenztiale des Doppelintegrals ab.
2] Die Reihenfolge der Integration ist auch nicht vvertauschbar. Wenn man die hintereinanderausführung der Integrationen vertauschen möchte ist es im Regelfall notwendig, das die Integrationsgrenzen neu bestimmt werden.
Eine Außnahme liegt vor, wenn alle Integrationsgrenzen normale Zahlen, sprich Konstanten sind, dann wird nämlich über einem "rechteckigen Integrationsbereich" integriert.
soviel zur Theorie!
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Mit freundlichen Grußen
N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 304
Registriert: 10-2002
| | Veröffentlicht am Samstag, den 01. Februar, 2003 - 15:47: | 
|
Ich hab hoit wenig Zeit, aber mich interriest das schon. Ich hatte letztens erts eine Paraboloidaufgabe, da kann ein Ellipsoid nicht schaden! Also von mir aus kanns losgehen!!!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 306
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 01. Februar, 2003 - 19:43: | 
|
Hi Ferdi,
schön, dann wollen wir uns an den Ellipsoid machen.
Wenn wir früher Ellipsoidenvolumina berechnet haben, so waren dies spezielle "Rotationsellipsoide". Entweder haben wir eine Normale Ellipse mit der Gleichung
(x²/a²)+(y²/b²)=1
um die x-Achse rotieren lassen- Das Volumen war dann
V=(4/3)pab²
um die y-Achse rotieren lassen- Das Volumen war
dann
V=(4/3)pa²b
Aber wie gesagt, das sind kein "Normaler Ellipsoid".
ein Normaler Ellipsoid hat die Gleichung:
(x²/a²)+(y²/b²)+(z²/c²)=1
wenn wir diese Gleichung nach z auflösen, dann erhalten wir folgende Funktionsgleichung:
z=f(x;y)=sqrt(c²-(c²/a²)*x²-(c²/b²)*y²)
Nun erhalten wir das Volumen auf ähnlichen Wege wie bei der Kugel.
VEll=2*ò ò sqrt(c²-(c²/a²)*x²-(c²/b²)*y²)dydx
vEll=8*ò0 aò0 y=(b/a)*sqrt(a²-x²)sqrt(c²-(c²/a²)*x²-(c²/b²)*y²)dydx
VEll=8c*ò0 aò0 y=(b/a)*sqrt(a²-x²)=wsqrt(1-(x²/a²)-(y²/b²))dydx
da Nun
(b/a)*sqrt(a²-x²)=w
(b²/a²)*(a²-x²)=w²
b²-(b²/a²)*x²=w²
1-(x²/b²)=w²/b²
VEll=8c*ò0 aò0 wsqrt((w²/b²)-(y²/b²))dydx
vEll=(8c/b)*ò0 aò0 wsqrt(w²-y²)dydx
vEll=(2pc/b)*ò0 aw² dx
vEll=(2pc/b)*(2/3)a*b²=(4/3)pabc
Voila;
Ich hoffe die Rechnung ist nach den vorhergehenden Beiträgen nachvollziebar!
Und das Ergebnis stellt uns auch zufrieden.
Für unsere Rotationselleipsoide gilt eben der Sonderfall das b=c oder a=c ist.
================================================
bis Später
Gruß N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 305
Registriert: 10-2002
| | Veröffentlicht am Sonntag, den 02. Februar, 2003 - 01:08: | 
|
Hi Niels,
ein würdiger abschluss des tages für mich! zuerst schien mir diese rechnung sehr konfus, aber als ich sie grade selbst zu meinen unterlagen getragen hab, war es dann doch eindeutig und sinnvoll! meiner meinung nach ist dieses thema auch gar nicht zu schwierig für mathe lk!
naja, danke erst mal für alles bis jetzt, freue mich schon auf weitere beiträge!
mfg
ps: auch dein dreifachintegral interessiert mich... |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 307
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 02. Februar, 2003 - 11:09: | 
|
Hi Ferdi,
dir wird sicher ein Tippfehler aufgefallen sein. es muss heißen:
(b/a)*sqrt(a²-x²)=w
(b²/a²)*(a²-x²)=w²
b²-(b²/a²)*x²=w²
1-(x²/a²)=w²/b²
mit dem Ergebnis habe ich auch weitergerechnet-sprich eingesetzt.
War wie gesagt nur ein Tippfehler im computer, dier Rechnung ist aber ansonsten korrekt!
Bis Später
Gruß N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 306
Registriert: 10-2002
| | Veröffentlicht am Sonntag, den 02. Februar, 2003 - 20:08: | 
|
Es war wohl doch wieder einmal ein wenig spät gestern abend! Naja, vielen Dank für deinen Hinweis. Irgendwie bin ich den ganzen Tag nicht ins Forum gekommen!
Naja, mann müsste ja diese Rechnung auch simultan bei Paraboloiden und Hyperboloiden durchführen können?
Naja, würde mich zum Abschluss auf ein Dreifachintegral zur Voluminaberechnung bei Kugeln freuen!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 308
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 02. Februar, 2003 - 20:13: | 
|
Hi Ferdi,
nu soll es um den Flächeninhalt gehen.
für f(x;y)=1 Beschreibt das Doppelintegral
òx=a bòy=fu(x) f0(x)dydx
das Volumen eines Zylinders mit der Höhe z=1 . Dieser Volumenbetrag ist aber Identisch mit dem Flächeninhalt der von den Funktionen y=fu(x) und y=fo(x) in den Grenzen von x=a und x=b begrenzt wird.
Beispiel aus früheren Zeiten.
Dder Würfel hat das Volumen V=a³ und die Grundfläche G=a². Für a=1 ist der Betrag des Volumens mit dem Betrag der Grundfläche überein.
Noch ein Beispiel:
Ein Zylinder hat das Volumen V=pr²*h und die Grundfläche G=pr². Für h=1 ist Der Betrag des Volumens identisch mit dem Betrag der Grundfläche.
So viel zum Verständnis. Morgen mehr.
Gruß N.
|
    
Leif (beckx)

Junior Mitglied
Benutzername: beckx
Nummer des Beitrags: 7
Registriert: 01-2003
| | Veröffentlicht am Montag, den 03. Februar, 2003 - 14:04: | 
|
Hi ihr beiden,
ich hab gerade mal eure Beiträge überflogen. Ohne Verwirrung stipften zu wollen schreib ich euch mal wie ich das Volumen einer Kugel bestimmen würde.
Volumenintegral einer Vollkugel in Polarkoordinaten:
p=phi
t=tetta
Int(x->y) sprich: Integral von x bis y
V=Int(0->R)dr Int(0->2pi)dp Int(0->pi)dt r² sin(t)
(r²sin(t))dr dp dt bezeichnet man als Volumenelement. Leider müsste ich eine Zeichnung dazu erst einscannen, doch ich glaube das sprengt den Rahmen hier...
Teilintgrale (in Kürze):
Int(0->R) r² dr = 1/3 R³
Int(0->2pi)dp = 2pi
Int(0->pi) sin(t) dt=-cos(t)|(o->pi)= 2
=> V= 4/3 pi R³
MFG
Leif |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 309
Registriert: 06-2001
| | Veröffentlicht am Montag, den 03. Februar, 2003 - 15:36: | 
|
Hi Leif,
du hast vollkommen recdht.
Aber soweit waren wir bei diesem öffentlichen exkurs noch nicht. Wir müssten dann uns anschauen, wie man 3D-Funktionen in Polarkoordinaten integriert. Wenn erwünscht unterhalten wir uns darüber später.
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 309
Registriert: 10-2002
| | Veröffentlicht am Montag, den 03. Februar, 2003 - 16:18: | 
|
Hi Niels,
ich bin jetzt wieder voll dabei. Hab jetzt alles noch mal durchgearbeitet. Es kann weiter gehen. In Polarkoordinaten muss ich mich erst noch einarbeiten, aber das dürfte kein Problem sein!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 310
Registriert: 06-2001
| | Veröffentlicht am Montag, den 03. Februar, 2003 - 19:44: | 
|
Gut,
also zur Flächenberechnung:
Wir gehen wieder nach dem "Baukastenprinzip" vor.
Wir setzen den Flächeninhalt aus infinizialen kleinen Flächenstücken dA=dy*dx zusammen.
Wir betrachten nun einen in der von y=fu(x) und fo(x) begrenzen parallel zur y-Achse liegendne "Flächenstreifen".
Wir erhalten die Fläche dieses Streifen indem wir alle Flächenstücke in y-Achse aufsummieren-sprich nach y zwischen fu als untere und fo als obere Grenze integrieren.
dAStreifen=(òy=fu(x) fo(x)dy)dx
Wir haben nun die Fläche eines Streifens der Breite dx berechnet. Nun summieren wir alle Streifen in x-Richtung zwischen x=a und x=b auf, sprich wir integrieren in x Richtung und erhalten die Gesammtfläche.
Ages=
ò ò dA
(A)
=
òx=a bdAstreifen
=
òx=a bòy=fu(x) fo(x)dydx
===============================================
Was das Für die Kreisfläche und Ellipsenfläche(Ellipse M(0;0)) bedeutet kann sich der geneigte Leser selbst vorstellen. Die Doppelintegrale lauten:
Kreisfläche:
AKreis=4*ò0 rò0 y=Ö(r²-x²)dydx
und
Aell=ò0 aò0 y=(b/a)*Ö(a²-x²)dy*dx
Wie gesagt die Berechnung nach obigen Schema ist dem intetessierten leser überlassen. Das Ergebnis ist aber eindeutig das gleiche wie Bei der normalen Kreisflächenberechnung oder Ellipsenflächenberechnung.
=================================================
Übrigens, diese "Technik" des Zerlegens von Mehrfachintegralen in mehrere einfache Integrationen hat auch einen Namen. Was wir dort gerade machen ist die Anwendung des "Satz von Fubini".
Bis Später!
Gruß N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 310
Registriert: 10-2002
| | Veröffentlicht am Montag, den 03. Februar, 2003 - 20:55: | 
|
Hi Niels,
ich als sehr interessierter Leser habe die Integrale berechnet! Für den Kreis habe ich die wohlbekannte Formel A=p*r² erhalten.
Für die Ellipse müssen wir das Doppelintegral noch mit 4 multiplizieren, da wir ja alle 4 Quadranten erwischen wollen. Ich erhalte wieder den alten bekannten: A=p*a*b!!
Freue mich auf weitere Beiträge!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 311
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 04. Februar, 2003 - 07:47: | 
|
Hi Ferdi,
stimmt natürlich, die 4 hatte ich bei der Ellipse glatt vergessen. Aber zum glück hast du ja aufgepasst!
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 312
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 04. Februar, 2003 - 15:09: | 
|
Hi Ferdi,
Mein weiterer Exkursplan sieht wie folgt aus:
wir schauen wiw wir Doppelintegrale in Polarkoordinaten berechnen (Allgemein)
Als Beispielaufgabe wollwn wir den Flächeninhalt der Kardioide berechen.
Danach Einführung von Dreifachintegralen und deren Berechnung in Kartesischer und Kugelkoordinatenform bzw Zylinderkoordinaten.
Gruß N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 311
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 04. Februar, 2003 - 15:48: | 
|
Alles klar! Kann losgehen!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 313
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 04. Februar, 2003 - 17:25: | 
|
Hi Ferdi,
wie sind den deine Kentnisse über Polarkoordinaten etc.?
sollen wir noch tifer ins Detail gehen oder gleich los integrieren?
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 314
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 04. Februar, 2003 - 20:28: | 
|
also,
ich denke wir könen sofort loslegen,
falls schwiriegkeiten auftreten,
kann ich mich ja melden,
aber ich denke es sollte klappen!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 318
Registriert: 06-2001
| | Veröffentlicht am Mittwoch, den 05. Februar, 2003 - 18:05: | 
|
Hi Ferdi,
gut, dann starten wir durch:
die "Transformationsformel" also die Umrechnungsformeln von x;y Koordinatensystem ins r;f Koordinatensystem sind dir wohl bekannt.
f(x;y)=f(r*cosf;r*sinf)=f(r;f)
Nun schauen wir uns den Integrationsbereich an:
Er wird durch 2 Strahlen f1 und f2 sowie 2 Kurven ri=ri(f) und ra=ra(f) begrenzt.
Das Flächenstück dA wird im Polarkoordinaten von 2 infinitial benachbarten Kreisen mit Radius r und r+dr und 2 infinitial benachbarten Strahlen f und f+df beschrieben. Daher gilt:
dA=rdrdf
Für ein Doppelintegral gilt daher:
ò ò f(x;y)dydx
(A)
=òf1 f2òri=ri(f) ra=ra(f)f(r*cosf;r*sinf)*r*drdf
=òf1 f2òri=ri(f) ra=ra(f)f(r;f)*r*drdf
Bei den Flächenberechnung machen wir analoge überlegungen wie bei den Kartesischen Koordinaten und kommen schmell zum Schluß, das für die Fläche gilt:
=òf1 f2òri=ri(f) ra=ra(f)r*drdf
Damit können wir ohne weiteres Den Flächeninhalt der Kardioide ohne Probleme berechnen.
Gruß N.
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 319
Registriert: 06-2001
| | Veröffentlicht am Mittwoch, den 05. Februar, 2003 - 19:34: | 
|
Hi Ferdi,
Wenn du willst können wir in unseren Exkurs ein kleines Leckelie zu Gemüte führen. Ich spreche von der Riemanschen Zetafunktion- Besser gesagt der Beweis, das
S¥ n>=1(1/n²)=p²/6
ist, natürlich per Doppelintegral.
Was hällst du von dem Vorschlag?
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 323
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 05. Februar, 2003 - 21:57: | 
|
Niels,
du hast wohl alles parat! Also ich bin für alles offen, da im Moment in der Schule nix los ist, kann ich viel zu Hause arbeiten!
mfg
ps: wie lang doch dieser thread schon ist.... |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 325
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 06. Februar, 2003 - 06:57: | 
|
Halt,
meinst du das Doppelintegral
ò0 1 ò0 1 1/(1-x*y)dxdy?
Wenn ja, dann brauchst du es nicht zeigen, ansonsten kanns weiter gehen!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 320
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 06. Februar, 2003 - 12:02: | 
|
Hi Ferdi,
du hast mich ertappt!
Ein Motto von mir ist:
"Man muss nicht alles wissen, man muss nur wissen wo alles drin steht."
Anscheinend hast du auch das "Buch der Beweise" buchstäblich im Regal stehen.
Sonst hätte ich dir das Werk empholen.
Nun gut, dann geht es mit den buchstäblich herzergreifenden Kardioiden weiter.
Bekanntlich sind Kardioiden "Herzkurven" - Icdh muss dabei immer an den Kardiologen im Krankenhaus denken:-)
Übrigens:
Bei uns an der Schule im LK ist es nicht anders. "Warten bis das Abi kommt" so könnte man die Stimmung derzeit beschreiben. und sonst passiert recht wenig.
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 328
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 06. Februar, 2003 - 12:49: | 
|
Ja,
das war der einzige gute Tipp den mein Mathelehrer mir in den letzten Jahren gegeben hat! Das Buch ist echt ein kleines Schätzchen!
Bin schon auf die Herzkurven gespnnt!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 321
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 06. Februar, 2003 - 18:38: | 
|
Hi Ferdi,
bevor wir zu den Herzkurven kommen sollten wir uns vorher noch einmal der Substitutionsregel für Doppelintegrale anschauen. Besser bekannt unter der Jacobi-Determinante.
Wir wollen uns sie erstmal anschauen.

Du kennst den Text aus dem Buch der Beweise.
Wir wollen die Regelung nutzen um nochmal die Formeln herzuleiten, die wir für Polarkoordinaten barauchen.
Bei uns ist:
x(u;v)=x(r;f)=r*cosf
y(u;v)=y(r;f)=r*sinf
Wir differenzieren partiell.
dx/du=cosf
dx/dv=-r*sinf
dy/du=sinf
dy/dv=r*cosf
Bilden die Jacobi Determinante nach angegebenen Schema und erhalten das verblüffende Ergebnis r .
Damit könnten wir den Gedankengang den wir bei der Herleitung von der Polarkoordinatenformel verwendet haben sehr einfsch nachvollziehen.
Es sollte wie gesagt nur ein kleiner Nachklapp werden.
Gruß N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 333
Registriert: 10-2002
| | Veröffentlicht am Sonntag, den 09. Februar, 2003 - 15:41: | 
|
Hi Niels,
ich bin wieder da aus meinem super Kurzurlaub. Falls du noch Lust hat können wir weiter machen mit Doppelintegralen und der Herzkurve!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 323
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. Februar, 2003 - 11:45: | 
|
Hi Ferdi,
wann der Exkurs fortgestzt wird hängt im Moment nicht von mir sondern von meinem Arzt ab. Ich muss zwar nicht zum Kardiolo9gen *g* , dber immerhin zum Hausarzt um mir Mittelchen gegen eine schwere Grippe zu besorgen.
Vielleicht kann ich Morgen früh den Beitrag lencieren.
Bis dann.
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 325
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 11. Februar, 2003 - 09:38: | 
|
Hi Ferdi,
es geht weiter:
die Gleichung der Kardioide-jedenfalls eine der möglichen Gleichungen der Kardioide-lautet:
r=2a*(1-cosf)
Für den Flächeninhalt der Kardioide gilt:
A=ò0 2p ò0 2a*(1-cosf)r*drdf
A=2a²*ò0 2p(1-cosf)²df
A=2a²ò0 2p(1-2cosf+cos²f)df
A=6pa²
================================================
Übrigens, das Thema Kardioide wurde hier im Board schon einmal behandelt. Damals aber ging es um Einfachintegrale. Der Beitrag findet sich im Archiv, genauso wie dieser Beitrag mittlerweile im Archiv ein Plätzchen gefunden hat.
Damals war das ein Beitrag von H.R. Moser!
Hier ein Ausschnitt:
[...]

[...]

[...]
Gruß N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 346
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 11. Februar, 2003 - 12:26: | 
|
Hi Niels,
ich habe leider keinen Archiv Zugang. Ich habe nur einen Artikel bestaunen dürfen, die anderen bleiben mir alle versperrt!
Ich habe auch mal wieder ein wenig rumgeforscht, und eine allgemeine Gleichung gefunden:
r=a*cos(f)+b
Ich habe versucht dies in kartesische Koordinaten zu übertragen, es ist mir nicht gelungen, es stand nur angegeben: (x^2+y^2-ax)^2=b^2(x^2+y^2)
Der Flächeninhalt ergibt sich hierfür allgemein:
A=[(p*a^2)/2]+p*b^2
Also für deine Kardiodie mit b=2a und a=2a sofort
A=6*p*a^2
Man kann doch theoretisch auch mit den kartesichen Koordinaten integrieren, schaut mir nur ein wenig umständlich aus?
mfg |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 348
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 11. Februar, 2003 - 14:04: | 
|
Hi,
ich noch mal. Hab grad mal versucht das kartesische aufzulösen und zu integrieren, kann man Vergessen, da kommt so ein mega ausdruck raus.
Naja, da is auch noch ein Vorzeichenfehler in meinem letzten Beitrag: es muss heißen für a=-2a kommt sofort das gewünschte ergebniss!
Man kann doch dann den Flächeninhalt eines Kreises berechnen durch:
ò0 rò-p p r dfdr
Dies liefert das Wohlbeannte p*r^2!
Hast du sonst noch irgendwelche schönen Doppelintegrale? Sonst könnten wir ja noch kurz zum Dreifachintegralübergehen?
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 332
Registriert: 06-2001
| | Veröffentlicht am Mittwoch, den 12. Februar, 2003 - 13:47: | 
|
Hi Ferdi,
a) Grundsätzlich sind Kardioide, wie andere algebraische Kurven, auch nicht nur in Polarkoordinatenform, sondern auch in Kartesischer oder Parameterform darstellbar.
Die Fläche muss also auch mit der Kartesische Form etc berechenbar sein. Nur sind diese Wege meist viel komplizierter.
b) Natürlich könnten wir noch diverse Doppelintegrale durchrechnen. Es gäbe da noch zahlreiche algebraische Kurven, oder man hätten noch diverse Kugelteile berechnen können.
Ich wäre auch dafür zu den Dreifachintegralen zu schreiten, auch wenn der Teil wirklich schwirig wird, weil im Gegensatz zu Doppelintegralen Dreifachintegrale im Allgemeinen keine geometrisch Anschauliche Bedeutung mehr haben.
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 354
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 12. Februar, 2003 - 14:36: | 
|
Also, dann auf zu den Dreifachintegralen. Wird schon klappen.
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 333
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 14. Februar, 2003 - 11:21: | 
|
Test,
anscheinend funktioniert das Board wieder:-)
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 334
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 14. Februar, 2003 - 13:21: | 
|
Hi Ferdi,
gut, wir gehen nun in den "Raum". D.h wir haben eine Funktion u=f(x;y;z) die einem Punkt in R³ einen Funktionswert zuordnet.Dabei ist die Funktion in unserem räumlichen Bereich stetig. Den Bereich, auch "Körper" genannt, teilen wir in n Teilbereiche. Wir wollen uns mit dem k-ten Teilbereich vom Volumen deltaVk nun näher befassen.
In diesem Teilbereich wählen wir einen Beliebigen Punkt Pk (xk|yk|zk) aus und berechnen an derren Funktionswert uk0f(xk;yk;zk) und bilden schließlich Das Produkt aus Funktionswert und Volumen deltaVk. Ebenso wird in anderen Teilbereichen Verfahren. Die Summe dieser Produkte, auch "zwischensumme" Zn genannt, hat keinerlei geometrische Bedeutung mehr.Sie lautet.
Zn=Sn k=1f(xk;yk;zk)*deltaVk
Wenn wir nun die Anzahl der n Teilbereiche gegen unendlich streben lassen, dann streben gleichzeitig die Volumina der Teilbereiche gegen Null. Falls dieser Grenzwert existiert wird er als 3-dimensionales Bereichsintegral, spriech als Dreifachintegral bezeichnet.
S¥ k=1f(xk;yk;zk)*deltaVk (deltaVk->0)
=
ò ò ò f(x;y;z)*dV
(V)
ò ò ò f(x;y;z)*dz*dy*dx
(V)
============================================
Die Berechnung solcher Integrale ist im Grunde genauso einfach wie bei Doppelintegralen. Man integriert hier auch von innen nach außen. Nur das man hier halt 2 innerer Funktionen hat.
soweit erstmal.
gruß N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 361
Registriert: 10-2002
| | Veröffentlicht am Freitag, den 14. Februar, 2003 - 14:32: | 
|
Aha alles klar. Wie sieht es hier mit der Vertauschbarkeit aus? Kann ich hier auch nur die Integration bei konstanten Grenzen vertauschen?
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 335
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 14. Februar, 2003 - 16:50: | 
|
Hi Ferdi,
ja du hast recht. Auch hier gilt, das die Integrationskonstanten nur vertauschbar sind, wenn sie konstant sind.
Gruß N.
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 336
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 16. Februar, 2003 - 10:49: | 
|
Hi Ferdi,
Dreifachintegrale haben nur einen geometrische Bedeutung, wenn gilt : f(x;y;z)=1 .
Dann beschreibt das Dreifachintegral
ò ò ò dV
(v)
bzw.
ò ò ò dzdydx
(v)
Das Volumen des Teilbereichs V.
Man kann sich das wieder mit dem "Baukastenprinzip" vorstellen. Diesmal sind es nicht Flächenstücke sondern Quarder mit den Kantenlängen dx ,dy und dz, die in allen Raumrichtungen hintereinander aufsummiert wwerden, sprich integriert werden, um dann´das Volumen des Körpers auszufüllen.
Wir wollen zum Abschluß nochmal auf diese Weise das Kugelvolumen, das ursprünglich mal den Anlaß zu diesem "Exkurs" gegeben hat, berechnen und damit den Exkurs beenden. Der Ansatz ist wieder vollgender:
Vk=8*ò0 r ò0 y=Ö(r²-x²)=w ò0 z=Ö(r²-x²-y²)dzdydx
Vk=8*ò0 r ò0 y=Ö(r²-x²)=wÖ(r²-x²-y²)dydx
Vk=8*ò0 r ò0 wÖ(w²-y²)dydx

für 0 eingesetzt wird die Stammfunktion Null.
Der Faktor wird vor das Integral gezogen:
Vk=2*p*ò0 rw²dx
Vk=2*p*ò0 r(r²-x²)dx
Vk=(4/3)*p*r³
=================================================
Ich finde das einen tollen Abschluß. Wenn noch fragen sind, dann sollen sie an dieser Stelle gestellt werden. Ansonsten möchte ich mich bei Ferdi für seine treue Zuhörerschaft bedanken.
@Ferdei:
Wenn du lust hast entwickel ich ein Kurs worin es um gewöhnliche Differentialgleichungen geht. Wenn du daran interesse hast, werde ich ihn vorbereiten und dich dann per Mail gegebenenfalls informieren, wenn es los geht.
viele Grüße
Niels |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 369
Registriert: 10-2002
| | Veröffentlicht am Sonntag, den 16. Februar, 2003 - 11:50: | 
|
Hi Niels,
a) Ich habe DIR zu danken, für deine aüsführlichen Erklärungen! Ich hätte nicht gedacht, dass meine Ausgangsfrage so Umfangreich bearbeitet wird!
b) Ich habe mich bis jetzt noch nicht so richtig mit Differentialgleichungen beschäftigt, würde mich aber über einen witeren Exkurs freuen!
mfg |
    
Klaus (kläusle)

Erfahrenes Mitglied
Benutzername: kläusle
Nummer des Beitrags: 240
Registriert: 08-2002
| | Veröffentlicht am Sonntag, den 16. Februar, 2003 - 12:10: | 
|
Hallo Niels, Ferdi!
Ich hätte auch Interesse an Differentialgleichungen!
MfG Klaus |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 337
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 16. Februar, 2003 - 12:12: | 
|
Hi Ferdi,
gut, dann werde ich den Exkurs ausarbeiten.
Ich habe noch eine Abschlußfrage an dich:
Was hat den bei dir der parallel Mathe LK noch mit Mehrfachintegralen gemacht? oder war des dann kein Thema mehr bei den?
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 371
Registriert: 10-2002
| | Veröffentlicht am Sonntag, den 16. Februar, 2003 - 12:24: | 
|
Also,
die haben einen Lehrer der hat denen das nur so gezeigt und dazu gesagt:
Ihr sollt das nur mal sehen, im Abi braucht ihrs eh nicht. Dann haben die kurz das Volumen berechnet und fertig!
Naja, wer versteht schon die Lehrer ;-)
mfg |





