| Autor |
Beitrag |
    
Friederike (Friederike)

| | Veröffentlicht am Dienstag, den 30. Oktober, 2001 - 14:40: | 
|
Hi Leute,
ich hab die Frage schon mal unter einer anderen Rubrik gestellt, aber vielleicht ist sie hier besser aufgehoben. Also
ich suche eine Kurve, die Parallel zu y=x²verläuft. Sie soll also überall den gleichen Abstand haben.
Aber wie bestimme ich z.B. den Abstand zwischen zwei Punkten??? Oder hat irgendjemand eine andere Idee, was man da machen kann??? BITTE Helft mir, das ist echt total wichtig!!!
Danke
Friederike |
    
Andreas

| | Veröffentlicht am Dienstag, den 30. Oktober, 2001 - 15:48: | 
|
Hi Friederike!
Wenn ich deine Frage richtig verstanden habe,
ist die Lösung sehr einfach:
y=x²+c
Die Punkte der beiden Parabeln haben dann
überall den Abstand c.
Ciao, Andreas |
    
Friederike (Friederike)

| | Veröffentlicht am Dienstag, den 30. Oktober, 2001 - 17:58: | 
|
Hi Andreas, leider ist d<as nicht ganz so leicht. bei deiner Lösung nähern sich die Kurven ebi x genen Unendlich immer mehr einander an, weil das c immer unbedeutender wird.
Ich suche aber eine Kurve, die immer den gleichen Abestand zu y=x² hat.
Aber trotzdem danke für den Versuch. Für weitere Ideen bin ich natürlich dankbar.
Bis dann
Friederike |
    
Friederike (Friederike)

| | Veröffentlicht am Dienstag, den 30. Oktober, 2001 - 17:59: | 
|
Hi Andreas, leider ist das nicht ganz so leicht. Bei deiner Lösung nähern sich die Kurven bei x gegen Unendlich immer mehr einander an, weil das c immer unbedeutender wird.
Ich suche aber eine Kurve, die immer den gleichen Abestand zu y=x² hat.
Aber trotzdem danke für den Versuch. Für weitere Ideen bin ich natürlich dankbar.
Bis dann
Friederike |
    
Cooksen

| | Veröffentlicht am Dienstag, den 30. Oktober, 2001 - 18:40: | 
|
Hallo Friederike,
für Deine Aufgabe hätte ich folgende Lösungsidee:
Abstände misst man senkrecht zur Kurve.
Es sei also P(xP;yP) ein Punkt der Parabel mit yP = xP². Dann hat die Tangente an die Parabel dort die Steigung 2xP. Ein Richtungsvektor u der Tangente wäre z.B.:
u = (1 ; 2xP)
(Vektoren sind fett, ihre Koordinatendarstellung kursiv geschrieben.)
Ein senkrechter Vektor dazu wäre:
n = (2xP ; -1).
Dies ist also ein Richtungsvektor der "Senkrechten" (Normalen) an die Parabel im Punkt P. Er hat die Länge Wurzel(4xP² + 1).
Wenn Du den Normalenvektor n durch seine Länge teilst und mit a aus IR multiplizierst, erhälst Du einen Vektor der Länge Betrag(a). Vom Punkt P gelangst Du zu einem Punkt Q(x;y) im Abstand Betrag(a), wenn Du
(x;y) = (xP;yP) + [a/Wurzel(4xP²+1)]*(2xP ; -1)
bildest.
Wenn ich Deine Problemstellung richtig verstanden habe, müssten die Punkte Q die Kurve bilden, die überall von der Parabel den Abstand a haben. Allerdings wird die Kurve mit Hilfe des Parameters xP beschrieben (yP lässt sich durch xP² ersetzen). Es gilt:
x = xP + [a/Wurzel(4xP²+1)]*2xP
y = xP² - [a/Wurzel(4xP²+1)]
Ich glaube nicht, dass es möglich ist, die erste der beiden Gleichungen nach xP aufzulösen und in die zweite Gleichung einzusetzen, um den Parameter zu eleminieren.
Für a größer Null erhält man bestimmt die erwartete Kurve "außerhalb" der Parabel. Was bei negativem a (insbesondere a < -1) passiert, weiß ich nicht.
Da kann man noch viel rumprobieren.
Cooksen |
    
Cooksen

| | Veröffentlicht am Dienstag, den 30. Oktober, 2001 - 23:07: | 
|
Hallo Friederike!
Ich hab noch ein bisschen weitergespielt und die Kurven für die Abstände a = 2, a = -1 und a = -1,5 zeichnen lassen. Hier das Ergebnis:
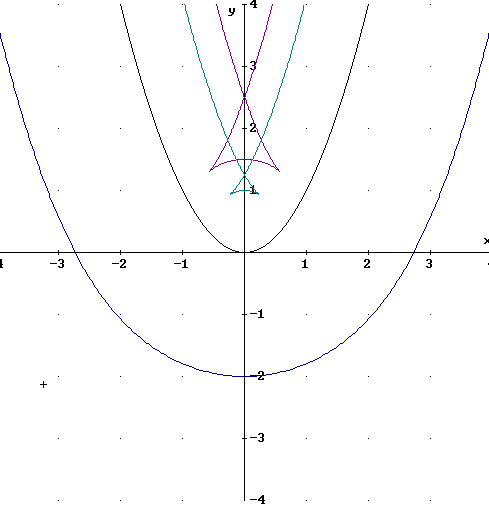
Cooksen |
    
Friederike (Friederike)

| | Veröffentlicht am Mittwoch, den 31. Oktober, 2001 - 09:08: | 
|
Das ist echt total cool!Danke!!! Leider hab ich die Herleitung noch nicht so ganz verstanden, weil wir das mit der Verktorrechnung noch nicht hatten.
Wenn du noch Lust hast, kannst du mir ja erklären. Aber das kann ich bestimmt auch aus irgendeinem Buch bekommen.
Also nochmal DANKE
Friederike |
    
Toby (Toby)

| | Veröffentlicht am Mittwoch, den 31. Oktober, 2001 - 16:30: | 
|
Hallo Friederike und Cooksen,
ich hätte da noch eine andere Idee, wie man die Aufgabe lösen könnte.
Ich zeichne einfach um jeden Punkt der Parabel einen Kreis mit einem konstanten Radius z. Die Kreisgleichung lautet: (y-ym)² + (x-xm)² = z², wobei ym = t² und xm = t ist, also erhalte ich eine Kreisschar mit dem Parameter t:
(y-t²)² + (x-t)² = z²
Für das Schaubild habe ich z=1 gewählt.
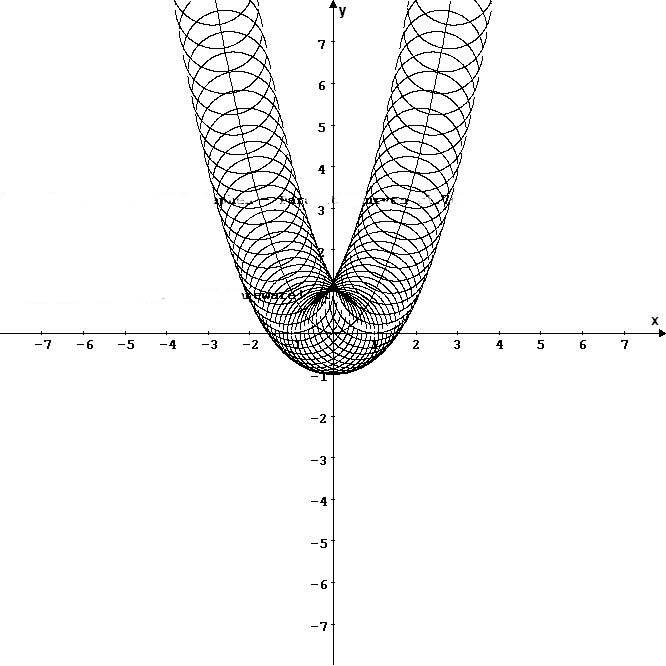
Mein Bild ist zwar nicht so schön wie das von Cooksen, das habe ich auch nur mit einer Shareware-Version von einem Funktionsplotter erstellt.
Die Kurven, die von der Parabel den Abstand 1 haben, erhält man als Einhüllende (Hüllkurven) der Kreisschar. Doch deren Berechnung ist in diesem Falle nicht ganz einfach, was ich auch nicht hinbekommen habe. Die Hüllkurve hat mit jedem Element der Kurvenschar nur einen Punkt gemeinsam. In diesem Fall gibt es 2 Hüllkurven, eine innerhalb und eine außerhalb der Parabel.
Die Kreise sind Tangenten an die Graphen der Hüllkurven. Man kann also auch - umgekehrt zum Hauptprinzip der Differentialrechnung - Tangenten betrachten und nach dem dazugehörenden Graphen suchen.
@ Cooksen: Ich vermute mal, dass deine Lösung eine Parameterdarstellung meiner Funktionenschar ist. Wenn man nämlich die Einhüllenden mit deiner Grafik vergleicht, sieht man doch die Ähnlichkeit, finde ich. Doch beweisen kann ich das nicht.
Viele Grüße Toby |
    
Cooksen

| | Veröffentlicht am Donnerstag, den 01. November, 2001 - 11:53: | 
|
Hallo Toby,
hab Dein interessantes Bild gesehen. Ja, so kann ich verstehen, wie das im "Innenbereich" der Parabel zustande kommt.
Hallo Friederike:
Einige Grundlage der Vektorrechnung kann ich Dir erklären:
Ein Vektor kann als Vorschrift für eine Verschiebung aufgefasst werden. Der Vektor u = (u1;u2) verschiebt jeden Punkt P(x;y) im Koordinatensystem um u1 parallel zur 1. Achse und um u2 parallel zu 2. Achse auf den Punkt P'(x+u1;y+u2).
Z.B. stellt der Vektor u = (2;3) die Verschiebung dar, die den Punkt P(3;4) nach P'(5;7) verschiebt, aber auch den Punkt P(-3;-1) nach P'(-1;2).
Verschiebungen/Vektoren lassen sich als Pfeile zeichnen, die bei P beginnen und bei P' enden. Es ist klar, dass verschiedene Pfeile, die gleich lang und parallel sind, dieselbe Verschiebung/denselben Vektor darstellen.
Zu jedem Vektor gehört seine Länge; das ist der Abstand von P zu seinem Bildpunkt P'. Nach Pythagoras ergibt sich im Koordinatensystem die Länge l des Vektros u = (u1;u2) zu l(u) = Wurzel(u1² + u2²). Statt von der Länge eines Vektors spricht man auch von seinem Betrag und schreibt Betragsstriche: l(u) = |u|.
Nur der Nullvektor 0 = (0;0) hat die Länge 0. Die zugehörige Verschiebung bildet jeden Punkt auf sich selbst ab.
Vektoren kann man mit beliebigen Zahlen a aus IR multiplizieren: a*u = (a*u1;a*u2). Dann vergrößert bzw. verkleinert sich die Verschiebung proportional zu a, aber die Verschiebungsrichtung bleibt erhalten bzw. sie kehrt sich um, wenn a negativ ist.
Die Gerade mit der Normalform y = mx + n hat den Anstieg m. Aus dem Steigungsdreieck liest man ab, dass der Vektor u = (1;m) jeden Punkt parallel zu dieser Geraden verschiebt. Dreht man das Steigungsdreieck um 90° im Uhrzeigersinn, erhält man ein Dreieck, dessen Hypotenuse senkrecht (normal) zur Geraden ist. Aus einer Skizze erkennst Du leicht, dass n = (m;-1) eine Verschiebung senkrecht zur Geraden darstellt.
Um die Länge eines Vektors u zu kontrollieren, dividierst Du ihn durch seine Länge: (1/|u|)* u und erhälst einen Einheitsvektor, also einen Vektor der Länge Eins. u darf natürlich nicht der Nullvektor sein. Durch Multiplikation mit a kannst Du so Vektoren beliebiger Länge erzeugen.
Ich hoffe Du kannst mit dem vielen Text was anfangen.
Gruß Cooksen |
    
Friederike (Friederike)

| | Veröffentlicht am Donnerstag, den 01. November, 2001 - 14:16: | 
|
Danke, euch beiden, ihr habt wir wirklich sehr geholfen!!!
Ich hab das auch schon fast verstanden...
Cooksen, bist du sicher,dass deine Zeichnungen richtig sind? Denn ich hab das nochmal ausprobiert, und es entsteht ein Knick in den Kurven.
Wer also noch Lust hat, weiter zu tüfteln ist herzlichst dazu aufgefordert;-)!!!
Bis dann
Friederike |
    
Cooksen

| | Veröffentlicht am Donnerstag, den 01. November, 2001 - 17:29: | 
|
Hallo Friederike!
Die Zeichnungen und die Rechnungen werden schon richtig sein. Aber wer kann von sich behaupten, dass er fehlerfrei ist.
Für a > 0 ergibt sich kein "Knick", das siehst Du auch in der Zeichnung. Für a < 0 ergeben sich bestimmt "Knicke" (wahrscheinlich ab a <= -0,5 ). Dies zeigt sich sowohl in Tobies Zeichnung als auch in meiner. Ursache ist, dass dann die parallele Kurve im "Innenbereich" der Parabel liegt und die starke Krümmung der Parabel im Scheitelpunkt.
Cooksen |
|





